Word Problem Activities
Activity 2.3.1
Models and Applications
Let’s Solve Some Word Problems with the Frayer Model
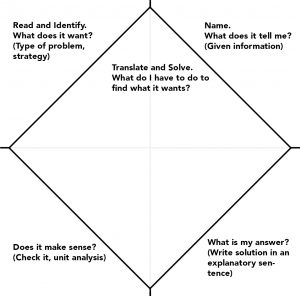
Use a Problem Solving Strategy for Word Problems
- Read the problem. Make sure all the words and ideas are understood.
- Identify what you are looking for.
- Name what you are looking for by choosing a variable to represent it.
- Translate into an equation. You can try to restate into a single sentence with all of the important information and then translate the sentence to English.
- Solve the equation using your algebra techniques.
- Check the answer in the problem and be sure it makes sense.
- Answer the question with a complete sentence.
Click here to go to Frayer Model Worksheet
Activity 2.3.2
Let’s solve different styles of linear applications
-
Geometry Problem
If 3 cm is added to the length of each side of a square, the perimeter of the new square is 40 cm more than twice the length of each side of the original square. What are the dimensions of the old and new square?
- Draw and Label a figure and write an expression for the new perimeter based on the drawing:
- Write an expression for the new perimeter based on the old perimeter.
- Create an equation based on the two expressions you wrote. Solve for the unknown and find the dimensions.
-
Solving for Distance, Rate or Time (DiRT) Problem
Maria and Ed work for a civil engineering firm and will be presenting a new technique they developed at a conference. Maria does not like how Ed drives since he always drives 5 mph faster than she does. They decide to drive separately from their own homes. The trip takes two hours for Maria and a half hour more for Ed since he lives forty miles further away. What is their respective average rates and distance traveled?
Fill out the table for this Dirt Problem. (d = rt)
| Name | Rate, r | Time, t | Distance, d |
|---|---|---|---|
| Maria | – | – | – |
| Ed | – | – | – |
Using the expression created for Maria’s distance from the table, write an expression that relates her distance to Ed’s. (Hint: how much further away if Ed from Maria?)
Write an equation that uses the above expression and the expression for Ed’s distance from the table and solve.
-
Solving For a Quantity in a Mixture Problem
Ben, the chemist, needs a 20% solution of hydrogen peroxide but only has a 15% solution. Searching through the lab, he finds 3 L of a 30% solution of hydrogen peroxide as well. How many liters of the 15% should Ben add to the 30% solution to get a 20% solution?
- Decide what your unknown is and fill in the rest of the table using the information in problem.
| Percent by Volume | Volume | Amount of Hydrogen Peroxide |
|---|---|---|
| 15% | – | – |
| 30% | 3 L | (0.3)(3 L) |
| 20% | – | – |
- Now create and solve an equation using the table. (Hint: the first two rows of last column should add up to the last row of last column).
-
Using a Formula to Solve a Mixture (PeRT) Problem
After going on Shark Tank, Joan now has $410,000 in profit from her company. She decides to invest part of it in some 6 month bonds that earn 4.65% annual interest and the rest will go into a stock account for one year that earns 4.91%. Joan wants to have a return on her investment of $14, 961. How much should she put into each investment to get this amount?
- This is a PeRT problem or I = Prt. For each row, the first three columns should multiply to the last. and fill in the information that you know
| Principal, P | Interest Rate, r | Time, t | Interest, I |
|---|---|---|---|
| x | 0.0465 | – | – |
| – | – | – | – |
| – | – | – | $14, 961 |
- Using the last column, create and solve an equation.
-
Using a Real World Linear Model

