3 Static Equilibrium Analysis: Using Matrix Algebra
3.1 An Introduction to matrices
Practice Problems
Problem 3.1.1: Write the following system of equations as a set of matrices:
![]()
![]()
![]()
Solution:

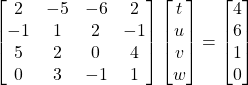
Problem 3.1.2: Write the following system of equations as a set of matrices:
![]()
![]()
![]()
![]()
Solution:
External Resources
Khan Academy: Introduction to Matrices
3.2 Matrix arithmetic
Practice Problems
Problem 3.2.1: Conduct each of the operations below given the following matrices:
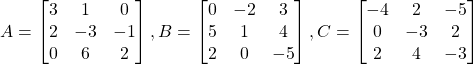
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
Solutions:
a) 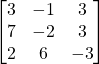
b) 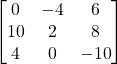
c) 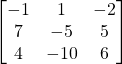
d) 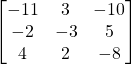
e) 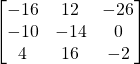
f) 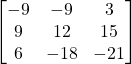
Problem 3.2.2: Conduct each of the operations below given the following matrices (the same as in problem 3.2.1):
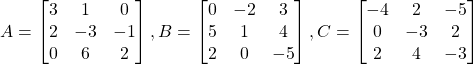
a) ![]()
Solution:
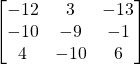
b) ![]()
Solution:
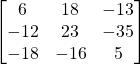
c) ![]()
Solution:
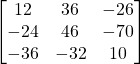
d) ![]()
Solution:
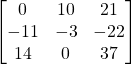
e) ![]()
Solution:
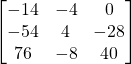
f) ![]()
Solution:
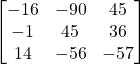
Problem 3.2.3: Can we multiply the following matrices? If not, why? If so, find the product.
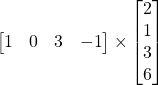
Solution: Yes.
![]()
Problem 3.2.4: Can we multiply the following matrices? If not, why? If so, find the product.
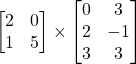
Solution: No. (2 columns for the first matrix and 3 rows for the second matrix.)
Problem 3.2.5: Can we multiply the following matrices? If not, why? If so, find the product.
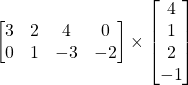
Solution: Yes.
![]()
Problem 3.2.6: Can we multiply the following matrices? If not, why? If so, find the product.
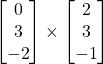
Solution: No. (1 column for the first matrix and 3 rows for the second matrix.)
External Resources
Khan Academy: Adding and Subtracting Matrices
Khan Academy: Scalar Multiplication
Khan Academy: Intro to Matrix Multiplication
Khan Academy: Multiplying Matrices
Khan Academy: Is Matrix Multiplication Commutative?
Khan Academy: Associative Property of Matrix Multiplication
Khan Academy: Zero Matrix
3.3 The transposE, identity, and inverse matrices
Practice Problems
Problem 3.3.1: Find the transpose of the following matrix. Is it symmetric, skew, or neither?
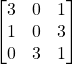
Solution:
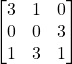
Neither.
Problem 3.3.2: Find the transpose of the following matrix. Is it symmetric, skew, or neither?
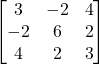
Solution:
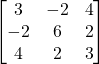
Symmetric.
Problem 3.3.3: Find the transpose of the following matrix. Is it symmetric, skew, or neither?
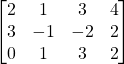
Solution:
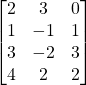
Neither.
Problem 3.3.4: Find the transpose of the following matrix. Is it symmetric, skew, or neither?
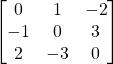
Solution:
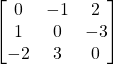
Skew.
Problem 3.3.5: Find the transpose of the following matrix. Is it symmetric, skew, or neither?

Solution:

Symmetric.
Problem 3.3.6: Consider the following matrices:
![]()
For each, determine what identity matrix is needed for both left-side multiplication (ex: IA) and right-side multiplication (ex: AI). Show that the identity matrix works.
Solution: For AI, use the 3×3 identity matrix. For IA, use the 2×2 identity matrix. For BI, use a 4×4 identity matrix. For IB, use a 1×1 identity matrix. For CI, use a 2×2 identity matrix. For IC, use a 2×2 identity matrix.
Problem 3.3.7: Determine if matrices A and B are inverses of each other.
![]()
Solution: Yes.
Problem 3.3.8: Determine if matrices A and B are inverses of each other.
![]()
Solution: No.
Problem 3.3.9: Determine if matrices A and B are inverses of each other.
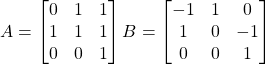
Solution: Yes.
External Resources
Khan Academy: Introduction to the Identity Matrix
Khan Academy: Dimensions of an Identity Matrix
Khan Academy: Using Identity and Zero Matrices
3.4 determinants: An Introduction
Practice Problems
Problem 3.4.1: Find the determinant of the following 2×2 matrices.
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
Solutions: 12, 33 ,6, -22, 47, -6
Problem 3.4.2: Find the determinant of the following 3×3 matrix using both Laplace expansion and the diagonalization shortcut.
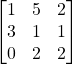
Solution: -18
Problem 3.4.3: Find the determinant of the following 3×3 matrix using both Laplace expansion and the diagonalization shortcut.
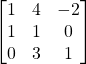
Solution: -9
Problem 3.4.4: Find the determinant of the following 3×3 matrix using both Laplace expansion and the diagonalization shortcut.
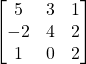
Solution: 54
Problem 3.4.5: Find the determinant of the following 3×3 matrix using both Laplace expansion and the diagonalization shortcut.
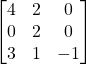
Solution: -8
Problem 3.4.6: Find the determinant of this 4×4 matrix. I will not ask you to do something like this on an exam!
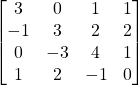
Solution: 23
Problem 3.4.7: Verify
![]()
using the following matrices:
![]()
Solution: Determinant is 26 (13×2)
Problem 3.4.8: Does the following matrix have an inverse? If it does…DO NOT FIND THE INVERSE!
![]()
Solution: Yes. (Determinant = 2)
Problem 3.4.9: Does the following matrix have an inverse? If it does…DO NOT FIND THE INVERSE!
![]()
Solution: No. (Determinant = 0)
Problem 3.4.10: Does the following matrix have an inverse? If it does…DO NOT FIND THE INVERSE!
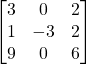
Solution: No. (Determinant = 0)
Problem 3.4.11: Does the following matrix have an inverse? If it does…DO NOT FIND THE INVERSE!
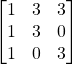
Solution: Yes. (Determinant = -9)
External Resources
Khan Academy: Determinant of a 2×2 Matrix
Khan Academy: Determinant of a 3×3 Matrix: Standard Method (Laplace Expansion)
Khan Academy: Determinant of a 3×3 Matrix: Shortcut Method
Khan Academy: Intro to Matrix Inverses
Khan Academy: Determining Invertible Matrices
3.5 Determinants: Finding the inverse
Practice Problems
Problem 3.5.1: Find the inverse of the following matrix, if it exists, using Laplace Expansion (using the adjoint matrix).
![]()
Solution:
![]()
Problem 3.5.2: Find the inverse of the following matrix, if it exists, using Laplace Expansion (using the adjoint matrix).
![]()
Solution:
![]()
Problem 3.5.3: Find the inverse of the following matrix using Laplace Expansion (using the adjoint matrix).
![]()
Solution:
Not invertible.
Problem 3.5.4: Find the inverse of the following matrix using Laplace Expansion (using the adjoint matrix).
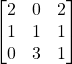
Solution:
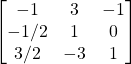
Problem 3.5.5: Find the inverse of the following matrix using Laplace Expansion (using the adjoint matrix).
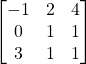
Solution:
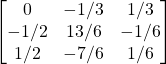
Problem 3.5.6: Find the solution of the following system of equations using Laplace Expansion.
![]()
![]()
Solution: x=-3, y=1
Problem 3.5.7: Find the solution of the following system of equations using Laplace Expansion.
![]()
![]()
Solution: No solutions exist.
Problem 3.5.8: Find the solution of the following system of equations using Laplace Expansion.
![]()
![]()
Solution: x=3, y=-2
Problem 3.5.9: Find the solution of the following system of equations using Laplace Expansion.
![]()
![]()
![]()
Solution: x=5, y=4, z=1
Problem 3.5.10: Find the solution of the following system of equations using Laplace Expansion.
![]()
![]()
![]()
Solution: No solution exists.
Problem 3.5.11: Find the solution of the following system of equations using Laplace Expansion.
![]()
![]()
![]()
Solution: x=-1, y=0, z=-5
External Resources
Khan Academy: Finding 2×2 Inverse Using Determinant
Khan Academy: Solving Linear Systems with Matrix Equations
3.6 Cramer’s Rule
Practice Problems
Problem 3.6.1: Find the solution to the following system of equations using Cramer’s Rule.
![]()
![]()
Solution: x=-3, y=1
Problem 3.6.2: Find the solution to the following system of equations using Cramer’s Rule.
![]()
![]()
Solution: No solution exists.
Problem 3.6.3: Find the solution to the following system of equations using Cramer’s Rule.
![]()
![]()
Solution: x=3, y=-2
Problem 3.6.4: Find the solution to the following system of equations using Cramer’s Rule.
![]()
![]()
![]()
Solution: x=5, y=4, z=1
Problem 3.6.5: Find the solution to the following system of equations using Cramer’s Rule.
![]()
![]()
![]()
Solution: No solution exists.
Problem 3.6.6: Find the solution to the following system of equations using Cramer’s Rule.
![]()
![]()
![]()
Solution: x=-1, y=0, z=-5
External Resources
No external resources for this section.

