7 Multivariate Calculus
7.1 Partial derivatives
Practice Problems
Problem 7.1.1: Find the partial derivative with respect to each variable in the problem below:
![]()
Answer:
![]()
Problem 7.1.2: Find the partial derivative with respect to each variable in the problem below:
![]()
Answer:
![]()
Problem 7.1.3: Find the partial derivative with respect to each variable in the problem below:
![]()
Answer:
![]()
Problem 7.1.4: Find the partial derivative with respect to each variable in the problem below:
![]()
Answer:
![]()
Problem 7.1.5: Find the partial derivative with respect to each variable in the problem below:
![]()
Answer:
![]()
Problem 7.1.6: Find the partial derivative with respect to each variable in the problem below:
![]()
Answer:
![]()
Problem 7.1.7: Find the partial derivative with respect to each variable in the problem below:
![]()
Answer:
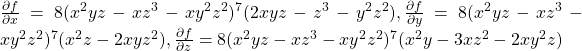
Problem 7.1.8: The production function for an economy is given below. Find the equation for the marginal productivity of labor and the marginal productivity of capital (MPL and MPK).
![]()
Answers:
![]()
Problem 7.1.9: An individual has the choice to consume different quantities of three goods. The utility function is given below. Find the marginal utility equations for each good.
![]()
Answers:
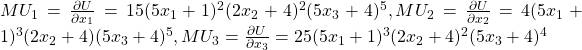
External Resources
Khan Academy: Partial Derivatives, Introduction
Khan Academy: Graphical Understanding of Partial Derivatives
Khan Academy: Gradients
7.2 Comparative statics
Practice Problems
No practice problems for this section. (Just be able to understand the derivation in the case study from class.)
External Resources
No external resources for this section.

