4 The Concept of the Derivative

4.1 Limits

Practice Problems

Problem 4.1.1: Evaluate the following limit:

$\lim_{x\to 5}x^2+3x-1$

Answer: 39

Problem 4.1.2: Evaluate the following limit:

$\lim_{x\to 3}\frac{x^2+5x+3}{x+6}$

Answer: 3

Problem 4.1.3: Evaluate the following limit:

$\lim_{x\to 2}\frac{x^2+x-6}{x-2}$

Answer: 5

Problem 4.1.4: Evaluate the following limit:

$\lim_{x\to 3}\frac{x^2-2x-3}{x^2+x-12}$

Answer: 4/7

Problem 4.1.5: Evaluate the following limit:

$lim_{x\to 2^-}\frac{5}{x-2}, lim_{x\to 2^+}\frac{5}{x-2}, lim_{x\to 2}\frac{5}{x-2}$

Answer: DNE (negative infinity), DNE (positive infinity), DNE

Problem 4.1.6: Evaluate the following limit:

$lim_{x\to 4^-}\frac{10}{(x-4)^2}, lim_{x\to 4^+}\frac{10}{(x-4)^2}, lim_{x\to 4}\frac{10}{(x-4)^2}$

Answer: DNE (positive infinity), DNE (positive infinity), DNE (positive infinity)

Problem 4.1.7: Evaluate the following limit:

$\lim_{x\to 5}\sqrt{5}$

Answer: DNE

Problem 4.1.8: Use the figure below to answer the following questions.

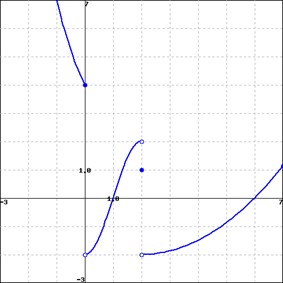
a) $\lim_{x\to 0^-}f(x)$
b) $\lim_{x\to 0^+}f(x)$
c) $\lim_{x\to 0}f(x)$
d) $f(0)$
e) $\lim_{x\to 2^-}f(x)$
f) $\lim_{x\to 2^+}f(x)$
g) $\lim_{x\to 2}f(x)$
h) $f(2)$
i) $\lim_{x\to 5^-}f(x)$
j) $\lim_{x\to 5^+}f(x)$
k) $\lim_{x\to 5}f(x)$
l) $f(5)$

Answer: 4, -2, DNE, 4; 2, -2, DNE, 1; 0.8, 0.8, 0.8, 0.8

External Resources

Khan Academy: Intro to Limits

Khan Academy: Estimating Limits from Graphs

Khan Academy: Estimating One-Sided Limits from Graphs

Khan Academy: Limits from Direct Substitution

Khan Academy: Limits from Factoring

4.2 Rates of change and the difference quotient

Practice Problems

Problem 4.2.1: Find the derivative of the following function using the difference quotient:

$f(x)=7x-5$

Answer: Derivative is $7$

Problem 4.2.2: Find the derivative of the following function using the difference quotient:

$g(x)=x^2-4x+2$

Answer: Derivative is $2x-4$

Problem 4.2.3: Find the derivative of the following function using the difference quotient:

$h(x)=-x^2+5x-\sqrt(3)$

Answer: Derivative is $-2x+5$

Problem 4.2.4: Find the derivative of the following function using the difference quotient:

$j(x)=x^3-x$

Answer: Derivative is $3x^2-1$

External Resources

Khan Academy: Formal Definition of a Derivative as a Limit

Khan Academy: Derivative of x² using the Formal Definition

4.3 Continuity and Differentiability

Practice Problems

No practice problems for this section.

External Resources

Khan Academy: Continuity Introduction

Khan Academy: Worked Continuity Example

Khan Academy: Differentiability and Continuity

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Student Companion for Mathematical Economics Copyright © by J. Zachary Klingensmith is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book