2 Computing and Computation
Computer science is not about machines, in the same way that astronomy is not about telescopes. There is an essential unity of mathematics and computer science.
Michael R. Fellows
As engineers, our interest in computer science leans toward the computer as a tool. We could argue that computer science is mislabeled. We are not interested in studying computers as much as we are in understanding how we might use the computer to model a system, or analyze a set of inputs.
For these cases, computer science would be more appropriately named Computational Science. We want to know how to use the computer to compute and after all, is that not what computation is all about?
So how are computing and computers different from computation? A computer is a device, usually mechanical or digital – although it does not have to be. While we commonly think of a computer as an electronic device, the computer could also be ourselves as human beings using our brains and perhaps our fingers and toes.
But computation is different from the computer. Computation is the process of making the computer, whether it is mechanical or digital, do our bidding; how we use it to perform the operations that are involved in calculating a result, or solving a problem, or modeling a system. Since our goal should also be efficiency, with computation comes the concept of complexity. Complexity relates to how long it takes to complete a task – or more specifically, how much longer it will take as the amount of data increases.
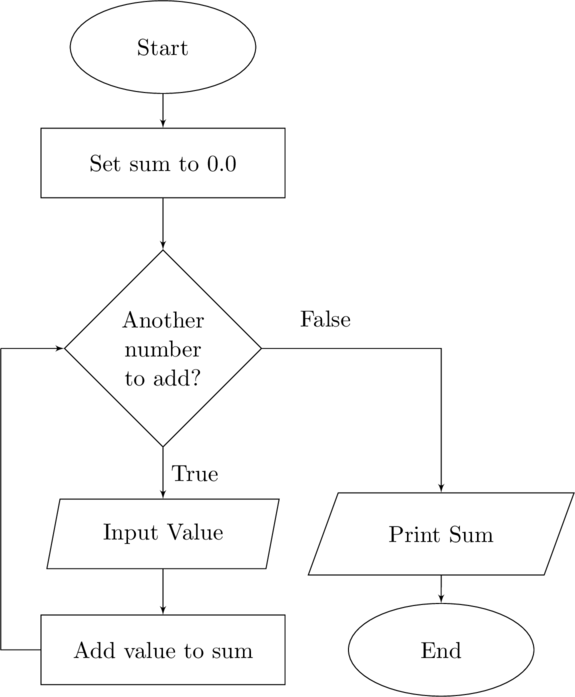
From this definition computers and computing are not synonymous – in fact they are very different. How we presently do computing can be extraordinarily complex but the idea of computing is quite simple. Computing is the process of turning data into information.
Computation is a simple concept – but far more than just adding and subtracting. It is the process of collecting data and turning it into information. In its most basic form computing or computation is synonymous with calculations such as arithmetic. While it is true that when you calculate you are processing data and are converting that data into information. But do not take the mechanics of arithmetic as absolute – computation is more than just arithmetic. It is any process that turns data into information. So while computation may involve calculations it may be something else, such as searching a database or plotting data into a graph.
Computation is the process of collecting data and turning that data into information.
For the sake of clarity what is data? And what is information? And how are they different?
Data
Data are the basic components of computing. The data are the numbers, the values, observations and facts from which we want to gain knowledge. While we assume that the data is correct it has no context. By itself, it is meaningless.
As an example, data might be the number of hits, walks, and runs that a baseball scored in a game. But until it is compared to the same data of the opposing team it has little value.
Or the data is the number and weight of trucks crossing over a bridge. By itself it is important but not something we can use directly make design decisions. but if we use the data to calculate stresses or strains on the cables supporting the roadway – processing the data into information – we can decide if the cables are an appropriate size or strength.
Information
Information is data with purpose. That is information is also data, but it is data that can now be used for decision making.
Information:
Information is data that has been processed, analyzed, organized, interpreted, or presented to give it purpose or put it into context. Information is intended to be used in making decisions.
As an example, you are given the numbers 3 and 5. This is data. The numbers are correct – as far as you know – but you cannot use them for anything because they have no context. They do not yet mean anything to you. But by the process of computing this data will become information.
Let us process this data. Five is the number of runs that the Baltimore Orioles scored in last night’s baseball game while three is the number of runs that the New York Yankees scored in the same game. Further, the difference between the two values is two and the larger of the two values was assigned to the Orioles. Now the data has become information. The information is that the Orioles won the game and did it by two runs. A strained example, but it follows the process of computing – transforming data into information.
The data that was entered into our system now has meaning. Computing, or computation, turned the data into meaningful information.
And with that meaning we can use our new found information to make decisions. This is computation at its most basic.
We usually think of data and information in terms of numerical values, such as the stress on a beam or the time until an event occurs, the definitions do not require us to force numerical values onto the data. We can just as easily manipulate nominal data – that is data that is presented as descriptions or names. As an example, a set of data might include Calculus, Statistics, Mechanics, Physics. The respective information that we join to this data is that these are required courses for an engineering student.
So if computing is turning data into information, what are computers? Computers are the tools with which we do computing.
The early static computers – such as rulers and protractors – were used as computers to increase precision.
For example, data may be the distance between two vertical sides of a door. A ruler turns this distance into a precise measurement – say 1.2 meters. Knowledge of the distance makes it possible for us to decide if we can move equipment through that door.
Mechanical computers did something similar. The Antikythera mechanism used the data in the form of the current date and time and processed it into the locations of several heavenly bodies.
An argument has been made that the Antikythera mechanism was a computer that instead of converting the time into the planetary locations, it did the opposite. The user would set the dials to the current locations of the planets and then be able to read the time.
Whether the computer is our fingers, a rule, a mechanical computer, or an electronic computer, there is a process that we must follow to perform computing. This process is known as an algorithm.
Every computing process requires following a set of instructions. For example our original idea of computing as basic measurement can be formalized as
StartPlace ruler at the leading side of the openingMark on the ruler the opposite side of the openingRead width of opening off of the rulerEnd
Algorithm to measure an opening
The set of instructions that you follow to perform computing – or solve a problem – is an algorithm.
Algorithm:
An algorithm is a clearly defined, finite set of instructions that when followed will perform a particular task.
An example of an algorithm is the sequence of steps that you need to add two two-digit numbers. This is the process – or algorithm – that most children are taught early in elementary school.
StartAdd the two right most digitsIf the sum is less than ten then record the sum and set carry to zeroIf the sum is greater than ten then record the right most digit of the sum and set carry to oneAdd carry and the two left digitsConcatenate this sum with the previous sum.End
Traditional Algorithm to add two numbers
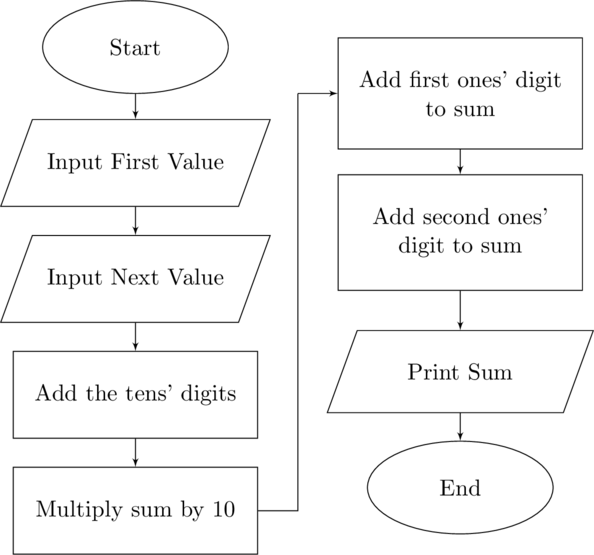
The algorithm in the figure Traditional Algorithm to add two numbers may be the common technique but like many algorithms there are other methods as well. A second algorithm – figure Bookkeepers Algorithm to add two numbers – for adding numbers was often used by bookkeepers when adding receipts.
StartAdd the two left most digitsMultiple the sum by tenAdd the first of the right most digits to the current sumAdd the second of the right most digits to the current sumRecord the valueEnd
Bookkeepers Algorithm to add two numbers
Both techniques accomplish the same task – adding two numbers together. But they do it in distinctly different ways. This does not invalidate that these are both algorithms. There is no requirement that there can be only way to complete a task.
What is important is that if many different bookkeepers follow the same algorithm on the same set of data they will calculate the same sum. No matter who, or what computer, follows the algorithm if they have the same data they must get the same result.
Every algorithm follows the same criteria.
- It shall have a single, clearly defined starting point.
- Each step is deterministic.
- It will reach a clearly defined end after a finite number of steps.
- It will account for any contingencies.
Why these criteria are important can be explained with an example of ten people traveling to the same location.
- A single, clearly defined starting point. Everyone who follows the algorithm must start at the same spot. What would happen if our ten people all had identical directions to follow, but each one started at a different location? They would start out going the same direction and turning at the same times, but they would be at different locations when they do each task. The result is that they would finish at ten different places.
- Steps are deterministic. What happens at each step cannot be left to chance. If different people follow the algorithm they must each have the same result. In our traveling example, each person who arrives at an intersection must make the same turn. If some randomly decide to turn left, while others turn right or continue straight, the again would finish at different locations.
- Ends after a finite number of steps. The algorithm cannot be open ended. If the traveling directions had a set of four right turns it is possible that our travelers would go in circles forever – an infinite loop.
- Accounts for any contingencies. What if during the trip there is construction and the road is blocked? The algorithm must be able to address necessary alternatives. This issue of contingencies brings up the possibility that for a particular set of data there is no solution. In that case the algorithm should allow for an end. If our travelers are flying, and the airport is socked in with fog, then their flight is not leaving. They have a choice to make – find alternative transportation or just go home. If they go home, then the algorithm ends despite not providing the desired result. In this case the algorithm has two ends – but still only one start.
An algorithm is a precise set of rules that describe the specific steps that will solve a problem. If you implement the algorithm correctly you are guaranteed to find the solution to a problem.
So how do we implement the algorithm? It is generic. It is not designed to be implemented by a specific person or on a specific computer. To do this we need to convert the algorithm to a form that can be understood by the device. We need to write a program. Thus, to implement the algorithm we run a program.
Semantically we often interchange the terms algorithm and program, But there is a slight difference. While the algorithm is a process that performs computing, the program is the specific, ordered set of instructions that when implemented will solve the problem.
In this case the program is a computer program; a program that is designed to be run specifically on a computer. But programming is a general term that involves any type problem solving. In fact, programs are the general name for any ordered set of instructions that need to be followed. This could be a computer program, or – from the field of optimization – what is known as mathematical programming, linear programming, or dynamic programming. Or, quite simply, a program is the list of names that present the order of performance of children at a piano recital.
The algorithm lays out the steps involved in the process. While we could just write out each step – this is often known as pseudo code, a common technique is to create a schematic of the program – a flow chart.
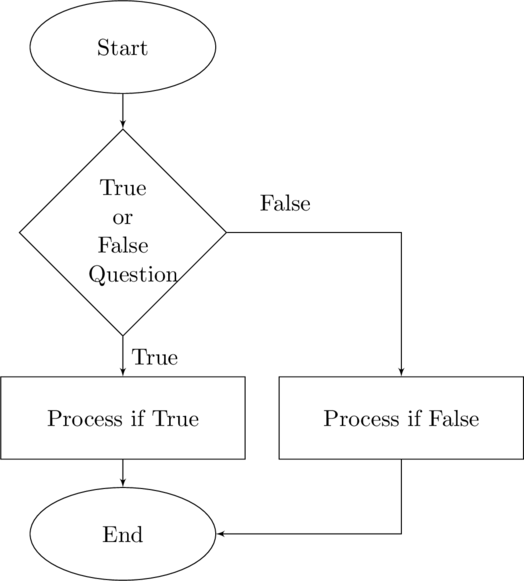
A flow chart is a schematic of an algorithm. It shows each step involved in the process with connections indicating the next action once a step is complete.
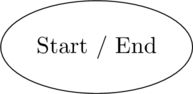
Flow charts are commonly written with a set specific geometric shapes for each the type of the action. Ellipses are used to indicate the Start and End; trapezoids for inputs and outputs, diamonds for decisions, and rectangles for executable – or action – steps.
Start and End are depicted as an ellipse
Inputs and Outputs are depicted as a trapezoid
Processes are depicted as a rectangle
Yes / No Questions are depicted as a diamond
Flow Chart Symbols
While there are many other symbols that used in flow charts, these four are the primary ones and the only that we will use.
Flow charts connect each node to another node. These connections are unidirectional and one to one – that is they may only connect one node with one other node. You cannot create a one to many node connection. Doing so would violate the rules of algorithms in that each action must lead to the same next action each time.
There is one action that at first appears to violate this rule – the decision diamond. When we implement the decision there will be exactly two paths; one for true or yes, and a second for false or no. This is still deterministic since there is only one path if the answer is yes and it is always the same path. The same holds for when the answer is no.
With one exception any descriptions are written within their shape. The exception is the connection labels for the decision diamond. Convention is that a small true or false be written next to the path. These labels are not actions so they are not placed inside of a shape.
There are three different structures that we will be using in flow charts and in our programs; the Sequential Structure, the Selection Structure, and the Repetition Structure.
Sequential Structure
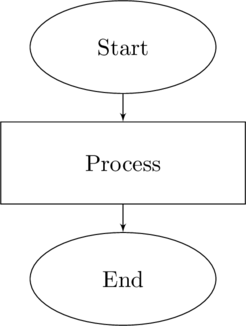
The most simple algorithm to be depicted in a flow chart is a sequential structure. A sequential structure is when each action in the algorithm follows directly from one to the next.
Flow Chart for Sequential Structure
“Begin at the beginning, the King said very gravely, and go till you come to the end: then stop.”
Lewis Carol in Alice in Wonderland
In a sequential algorithm the order of the actions are important. If you change the order then the results you would expect the results to be different.
Sequential Structure:
A sequential structure is a programming structure in which each step follows a linear path from start to end.
In its most simple form, in the figure Flow Chart for Sequential Structure, the sequence is Start – Process – Stop. This is linear – each step follows the same one that immediately precedes it. If you run the program multiple times it will follow the same steps in the same order every time.
We have already seen a flow chart that implements a sequential algorithm. The figure Computation is the process of collecting data and turning that data into information depicting the process of computing – turning data into information – is a sequential structure.
Another example is the bookkeeper’s algorithm (in the figure Bookkeeper’s Algorithm to add two numbers). The algorithm can be written as a flow chart using a sequential structure (in the figure Flow Chart for the Bookkeeper’s Algorithm)
Flow Chart for the Bookkeeper's Algorithm
Recall that the sequential structure is linear – it never leaves the same path. But what if there are exceptions? Perhaps a number is negative in which case you should subtract the digits. This requires a second structure – a selection structure.
Selection Structure
The sequential structure provided a means for following a specific set of steps – one after the other. Every time that the algorithm is run the results are the same. But it often occurs that a decision must be made. Perhaps a low temperature requires a furnace to be turned on. Or a pathway is blocked and an alternative will have to be followed. Or in the case of the Scarecrow from the Wizard of Oz, you simply have a preference of one over the other.
Selection Structure:
A selection structure is a programming structure in which a true – false (yes or no) question is asked. The answer determines which of two paths the algorithm will take.
To incorporate this decision making ability to an algorithm requires a second structure – the selection structure or what is commonly called the branch.
Flow Chart for Selection Structure
An example of the use of the selection structure in the Bookkeeper’s Algorithm is dealing with negative values. The sequential structure is fine when each value is positive – you just add to the running total. But if it is a debit instead of receipt you would subtract it from the total. Since you would be subtracting twice – first for the tens value and then for the ones value – the algorithm needs to know whether to add or subtract. We can do this by adding in a selection.
There is an argument that it is this decision making process in the selection structure that makes a computer reason. While it is true that this is the foundation of artificial intelligence it is far from true reasoning. The reason for this is in the ability of the selection structure.
Warning: The decision controlling the branch of a selection structure is binary. It can only take on one of two possibilities. In this any question must be answerable as Yes or No, True or False, or 1 or 0.
The decision component in the selection structure asks a type of question; Is the number negative?, or Is the fruit an apple?. This is similar the game of twenty questions. Each question must be answered as Yes or No, or True or False, or using integers 1 or 0. That is it. They questions are not open or free response. This means that you cannot ask questions such as What would you like for lunch?, but you could ask Would you like a peanut butter and jelly sandwich?
What if we have three numbers to add, or four, or a hundred? The algorithms that we have been demonstrating sequence and branches, but what if we need to repeat? This requires the third structure – the repetition structure.
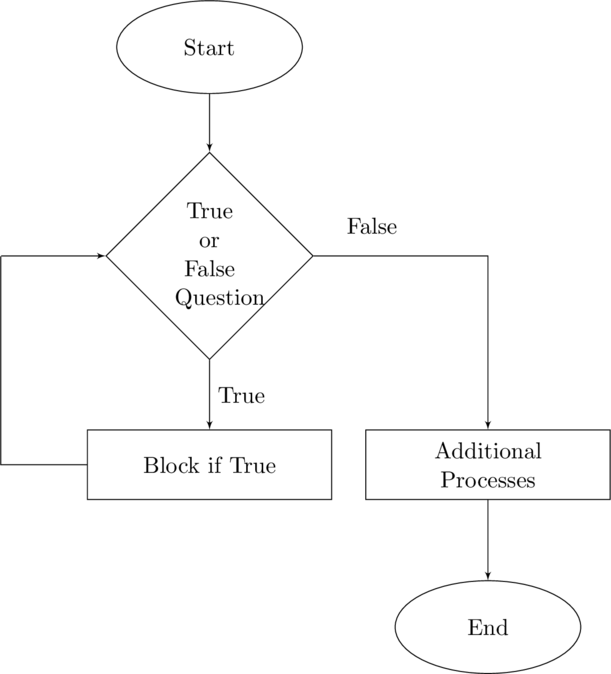
Repetition Structure
A computer does not do anything any of us could not do. It just does it over and over again without complaining
David Barron
There is nothing that a computer program does that a person could not do themselves given enough time. The value of computing is not necessarily that the computer can calculate very quickly but that it can do the same calculation hundreds or millions of times. A person would never do that. The application of performing the same operation multiple times employs a repetition structure.
Flow Chart for Repetition Structure
Extending the addition of a sum of numbers algorithm, a repetition structure could be employed if instead of two numbers we are adding three, or four, or one hundred. We could assume that we do not know have prior knowledge of how many numbers are to be added. The repetition structure would then run as many times as we have numbers.
Repetition Structure:
A repetition structure is a programming structure in which a set, or block of instructions are repeated multiple times.
Flow Chart for Using Repetition to Add Several Numbers
The flow chart in the figure Flow Chart for Using Repetition to Add Several Numbers is shorter than the sequential approach. But more importantly it is open-ended. We could have extended the sequential structure for adding numbers to any amount, but whatever that number of values is we would be stuck with it. If we wanted to add different number of values we would have to change our algorithm.
For the sake of simplicity, the flow chart using repetition is for adding a set of numbers. We could change this algorithm to the bookkeeper’s algorithm by adding two repetition structures. The first would be for adding the tens digits then a second for adding the ones.
We have seen three different structures for depicting an algorithm. Further we took note that if we replaced the sequential structure with a repetition we could make the addition algorithm more versatile. But we should also be interested in the efficiency of the algorithm. Is there one structure that is more efficient than another?
An algorithm identifies each action to be taken, but as was shown there can be more than one algorithm for a particular task. So which to use? The choice of algorithm may come down to several items. Which algorithm is the easiest to understand? Which is easiest to implement? Which is the most efficient in terms of the number of computational steps involved? Which algorithm is the most efficient in terms of the amount of space – or memory – required to implement it?
In analyzing an algorithm we must take into account two items; the amount of memory that will be used, and the number of steps that it will take to complete the algorithm. The memory is known as spatial complexity while the number of steps is the algorithmic complexity or computational complexity.
The number of steps is not the same as the amount of time. The steps in an algorithm is independent of the platform on which the program is being run, while the time is dependent upon the processor speed. A program on a slow computer or fast computer will still have the same complexity.
Comparing the complexity of different algorithms is done by creating a function of the number of steps with respect to the size of the input. If an algorithm has

data inputs then the complexity would be
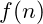
. As an example, two algorithms may have two complexity functions;
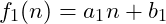
and
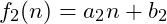
. Depending upon the values of
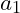
,
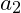
,
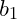
, and
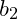
one of these algorithms may use fewer steps or more steps than the other.
While it is tempting to calculate the actual number of steps, or the amount of memory, the actual number of steps is not what is important – the rate of change in the number of steps is. Being the rate of change, complexity is the first derivative of the number of steps. Further, the actual values are not of interest. Complexity is a relative measure.
| Complexity |
Running Time |
Example |
| Constant Time |
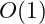 |
Calculating the median of a set of values |
| Logarithmic Time |
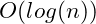 |
Searching an ordered set of values |
| Linear Time |
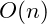 |
Calculating the mean of a set of values |
| Log-Linear Time |
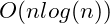 |
Comparison sort algorithm |
| Quadratic Time |
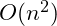 |
Bubble sort algorithm |
| Polynomial Time |
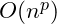 |
Set of nested repetition structures |
| Exponential Time |
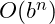 |
Brute force password attack |
| Factorial Time |
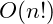 |
Traveling salesman problem |
Table: Ordered list of algorithmic complexity
The rate of change is described by the term with the largest first derivative. For example, if the number of steps is
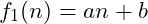
then the magnitude of the derivative is controlled by
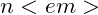
, the linear term. Because of this the number of steps – or complexity – will increase linearly as the amount of data increases. Another way of looking at this is to ask “How much longer will the algorithm take if the amount of data doubles? or increases by a factor of
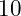
? For the linear algorithm if the amount of data doubles then
(1) 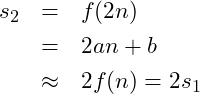
which is approximately double the number of steps for
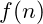
. If the amount of data increases by a factor of ten then the number of steps is about ten times the number of steps for
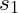
. The complexity for this algorithm is described as
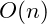
– read as “Big O of n”.
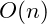
is also known as linear time. This means that the number of steps is a linear function of the amount of data.
Constant Time
The fastest algorithms operate in
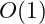
time; known as constant time algorithms. While it is often erroneously thought that the algorithm takes a single step, it in fact takes a constant number of steps. This constant could be any value. As a function, if there are

items of data the algorithm takes
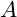
steps. In this case increasing the amount of data – have the amount of data grow from

to
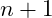
– the number of steps does not change. It is still
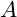
.
Median:
The median is the value that divides a sorted set of data into two equal sized halves. If the number of observations is even then fifty percent of the observations are below this value and fifty percent are above. If it is odd then the two halves consist of fifty percent of the observations not including the median value itself.
An example of a constant time algorithm is determining the median of a sorted set of values. If you have a list of
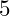
values and they are sorted from the smallest to the largest then the median value – the value at which half of the data is below and half is above – is
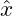
where
The formula for the median shows that the number of observations – the data – is not a factor in the algorithm; only knowledge of the value for the number of observations is. If
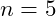
, or
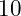
, or
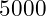
the number of steps remains the same.
Example
A class of forty one students are sorted by their height. Each one is sitting in a numbered seat – say from 1 to 41. The professor wants to find the the student with the median height.
The median will be the student in seat 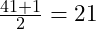 . The professor asks student twenty one to stand.
. The professor asks student twenty one to stand.
Now there are 287 students again sorted and in numbered seats. The median height student is the one in seat
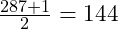
. It took the same number of steps despite there being seven times the number of students in the data set.
Logarithmic Time
Between constant and linear time is a complexity known as logarithmic time,
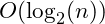
. An example of a logarithmic time algorithm is a binary search. A binary search is done on an ordered set of data. To find the location of a particular key the algorithm first checks the middle most value. If the key is smaller than the middle value then all of the upper half is ignored and the binary search is repeated on only the bottom half. This is repeated until the value is found or there are no more elements in the set.
Binary Search:
A binary search algorithm is one in which a sorted set or list or array of data is searched by checking the middle most observation. If the comparison does not match this value then either all data below or above is excluded from the search and only the remaining half is searched. The binary search has a complexity of 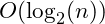 .
.
The speed of the the logarithmic time algorithm is easily calculated. Since the binary search eliminates half of the remaining data each step, a data set with
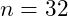
will have
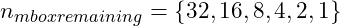
with each pass. This means a worst case search time of
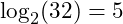
passes. A recursive form of the binary search algorithm will be presented in chapter 8.
Linear Time
As mentioned before, an algorithm that is slower than logarithmic time is linear time, 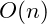 . This is a common complexity for a single repetition structure or loop.
. This is a common complexity for a single repetition structure or loop.
An example of a common linear time algorithm is the calculation of the arithmetic mean of a set of data.
This calculation can be done using a single repetition structure. For each additional observation the algorithm will require an additional step, thus
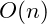
Log-Linear Time
There are many algorithms for sorting data. While it is possible in a specific case to sort a set of data in linear time, sorting algorithms are commonly slower than
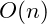
. The fastest of these is the comparison sort.
A
comparison sort functions in
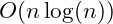
or what is known as
log-linear time or
sub-linear time because while slower than a linear algorithm it is still faster than
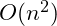
.
Quadratic Time
A second sorting algorithm – and one that is commonly taught because of its ease of programing – is the
bubble sort. It runs in
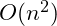
or
quadratic time.
The bubble sort is an example of an algorithm that is implemented using two nested – one inside of the other – repetition structures. Two nested loops, running in 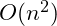 time, is an example of a quadratic time algorithm.
time, is an example of a quadratic time algorithm.
Polynomial Time
The quadratic time algorithms are members of a set of algorithms know as
polynomial time algorithms or
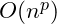
where
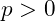
is a constant.
Any algorithm that is polynomial time or faster is considered operational. That is it can be programmed and for increasingly large amounts of data can still be run to completion. This may appear paradoxical since there is not upper bound on
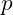
. Clearly there is a difference between a
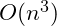
algorithm and one that is
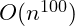
. And there is, but they both will run to completion.
The issue – and a reason for our interest in algorithmic complexity – is that of algorithms that run in non-polynomial time.
Exponential Time
A common issue confronting all of us is security. Let us start with a simple example. A combination bicycle lock takes four digits. Since there are ten possible digits for each there are
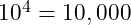
different combinations. A computer algorithm to crack this would only need to try
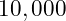
different combinations.
But what if instead of four digits we require eight? Then the growth in the number of steps to crack the lock just increased to
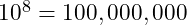
different combinations.
The growth in the number of combinations that the computer would need is an example of exponential complexity. In this case it is
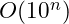
. The general form for exponential complexity is
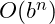
where
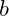
is an unspecified constant.
It is the challenge of exponential complexity that can make computer passwords more secure. While many companies require passwords to be a minimum of eight characters with mixes of upper and lower case, numerical digits, and characters, these passwords still come under the cutoff for a fast computer to crack – and are of course very difficult to remember.
The alternative may not be to make the password more complicated by mixing letters and characters, but simply to make it longer. If the only requirement is that the password be at least twenty characters long, then there are
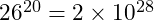
different passwords. And while twenty is not actually all that long the exponential complexity of a brute force attack makes it difficult to break.
Another example of an exponential time algorithm is the recursive Fibonacci function. This algorithm is
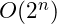
. We will look at this in chapter 8.
If

is small, a
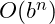
algorithm can be completed. But recognize that for each addition data point the number of steps increases by a multiple of
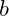
. This rapidly increase in the time makes any algorithm with a much more data completely unusable.
But while an exponential time algorithm is unusable for all but the smallest data sets, there is a common time complexity that it even worse.
Factorial Time
Traveling Salesman Problem:
Given that there are  cities with known distances between each city, what is the shortest possible route that a person can visit each city and return their starting point? The Traveling Salesman Problem – TSP – is a common example of a factorial time algorithm.
cities with known distances between each city, what is the shortest possible route that a person can visit each city and return their starting point? The Traveling Salesman Problem – TSP – is a common example of a factorial time algorithm.
There is a famous problem in which a traveling salesman must visit

cities. The goal is to find the path that connects all of them that has the minimum distance. The brute force approach is to start a city then go to every city, recording the distance. You then move to a new starting city and repeat this, continuing on until you have travelled from every city in the network to every other city. If there are

cities then this algorithm will take

steps. As such the algorithm is
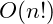
known as factorial time.
The complexity – or running time – of an algorithm is important not for what it tells us about the actual number of steps, but for when it tells us that an algorithm is unusable. While polynomial time algorithms may appear to be inefficient –
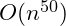
is a polynomial time algorithm – they can still be coded and run to completion given a reasonable amount of time. So even as the amount of data increases the number of steps also increase but not so fast that the time grows out of control.
In reality, an algorithm that is
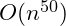
is an outrageous number of steps but it is still polynomial time. The reality of programming is that in engineering it is unlikely that we would ever have a polynomial algorithm that is slower than
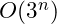
. This would be the complexity if you have three loops nested one in inside of the other. You might have this if you were programming a finite element analysis in three space.
While polynomial time algorithms tend towards
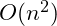
and possibly
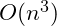
, there are common models that go beyond the polynomial time into exponential and factorial time algorithms. Unless the size of the data set is extremely small the amount of time that these algorithms would take to run to completion would often be beyond our abilities – for even the fasted computers. As a result there are many non-polynomial algorithms in which active research is to develop an alternative that will run in polynomial time. Until that time, if you know the algorithm is exponential or factorial it is probably best to step back and look for an alternative model.
Creating a flow chart is a step in the process of creating an algorithm. But most of the time our goal is a bit more. We want to create a computer program to assist us in an engineering analysis, or in modeling a system, or as part of a design process.
Too often when writing a computer program we take an approach similar to one (and just as wrong) as we do when writing a composition for an English class. The professor tells us all of the steps involved in creating writing such as brain storming, outlining, writing rough drafts, and so on, but in the end we just start writing the composition.
Programming is similar in that when we have to write a program we just start writing it – without much thought to how or why. Instead we can follow the standard approach of an engineering design.
There is a process that we, as engineers, use as part of the design process. We
- Define the problem
- Specify the requirements
- Build a prototype
- Build the product
- Test the solution
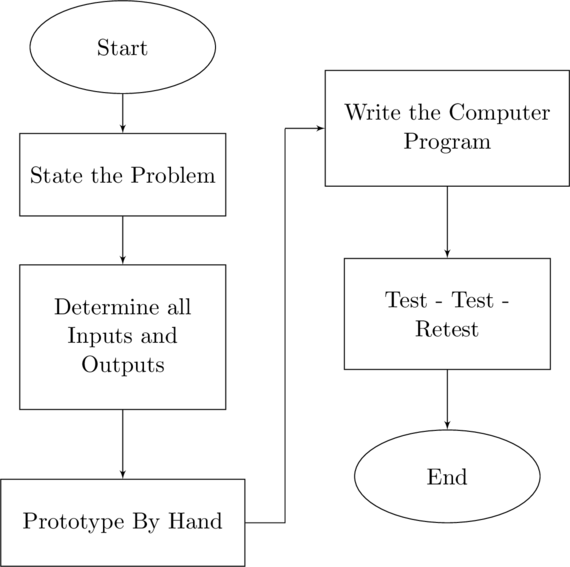
The engineering design process is directly adaptable to writing computer programs. It does not matter if we are writing a short code or building a large software project, the process is similar – just a matter of scale. Stating the problem is exactly the same. The specifications and requirements for a design project become understanding the inputs and outputs of the program. Building a prototype becomes working out a solution by hand. The final product is actually the most similar – building the product and writing the program are the same idea. A flow chart of the engineering programming design process is shown in figure Engineering Design Process
Engineering Design Process
Whether we are building a bridge or designing a manufacturing line the five steps are self explanatory. But what do they mean with respect to writing software?
State the Problem
The first step is also the one most likely to be overlooked. We are already convinced that we know what the program must do, but do we? A statement of the problem to be solved can often provide a path that will need to be followed, including the many steps that might be overlooked if you had just started to write the program. The simple step of stating – and perhaps outlining – the problem can solve hours, days, or weeks of adding new code or rewriting the code after the fact.
Determine the Inputs and Outputs
Much like the previous step of stating the problem, we often jump into coding without a clear idea of what data will be needed to run the program and what information will be created when it is done. We will as we develop programming techniques that a common style is is to group all of the inputs and later the outputs together. If we are clear at the start what inputs and outputs we will need we can start our program by creating the necessary code to enter the data and return – commonly print – the information. With this done we will know what we call all of the inputs and outputs, and as important we do not have to add input or output code as we developed the program.
Write the Program
It took three steps but you are finally at the point where you would actually write the computer program. If you have followed the process this step should be direct – you have all the details that you need for your code.
There is also are also possible sequences that you can follow in writing your program. By having the plans in place – perhaps creating a flow chart you could save hours or days on coding. If you are working alone then you will be responsible for the entire program. In this case there is an approach to coding that can be beneficial.
Teaching a dog to swim
If you want to teach a dog to swim you need to address the question what do I teach first? The common responses are to teach them to get into the water, or to dog paddle, or just to float. In fact the first lesson should be on how to get out of the water. If the dog cannot get out then all of the lessons are for naught.
There is a paradox in computer programming. It is where do we start? The conventional wisdom would be to start at the beginning just like we did when designing an algorithm and creating a flow chart. But this is actually backwards. Much like teaching a dog to swim we need the end results first. Thus we do not start with creating inputs or even calculations, but instead we start by creating the output.
The first step in writing a program is to return all of the outputs. It does not matter that you do not have any input data or calculations or the information that you will be returning or printing. Make up output information that will act as a temporary placeholders until the real information is available. You can even go so far as to work in all of the formatting so that the output – when it is using real information – looks just the way you want it.
The next step is actually the middle step. Now create fake input data and work on the computations or analysis. This way you have consistent inputs and do not have to repeatedly enter them into the program. If they are hardcoded they will not change and you can save hours entering and reentering the same data.
The final step in writing the program is to create the start – the data input. Since the rest of the program is done all that is required here to create the interfaces for data input. This could be by having a user enter the data, or by having the program read or access the data from some other source. What is important in this step is data integrity. Is the data that is being used correct? This is where all of the initial data checking and verification will take place
Once the data input is complete, is the program done? Sadly, no. Now comes what may be the most challenging step of all – Quality Control. You need to start testing.
Test – Test – Retest
If the program has been written, why is there an additional step? The reality of any computer program is that if there is a problem with it, the programmer will be blamed. And the chances are always good that there is a problem. Thus the quality control step for even the most simple program.
When you test you need to perform multiple tests. This usually involves changing inputs to the model. You need to test the common – the inputs to the program would be expected. For example, if the model expects temperatures to be between twenty and one hundred degree, then run the program with many values between twenty and one hundred degrees. The goal in this case is to determine if the program works as expected when it is used as expected.
But you should also test it against the extremes. While twenty and one hundred might not be expected, they are still possible – albeit rare – and should be tested as well.
But the third case is that of nonsense. If the input can never be below twenty, then test values of zero, or negative values. The same applies to the other other extreme. If the maximum possible value is one hundred then it is important to also check one thousand, or one million. In these cases the program should probably catch the input error to ensure that the input could not happen. While these values should never be entered into the program under normal circumstances, a user could enter them by mistake. Since the user did not enter these values on purpose, the chances are great that they would not know that they had made the error. Thus it is up to the program deal with this type of error.
Testing is meant to identify errors in the program so correcting the errors would be the natural progression from testing. But correcting an error requires knowledge of the type of error.
Programming errors can be classified as three types; syntax errors, run-time errors, and logic errors.
Syntax Error
The first type of possible error is the syntax error. This is commonly thought of as a typo, or a misspelling. It occurs because the program statement has been written incorrectly. As such the computer cannot process and execute the statement. Since the individual statement cannot execute, a program with a syntax error will not run to completion.
Syntax errors do not require much more testing than trying to run the code. If the program does not run then there is a good chance that there is a syntax error. Most compilers and interpreters will indicate line where the syntax error is. Common syntax errors occur when a variable name or a command is misspelled. Another might be missing a close such as a } or the word end on a block of code.
Runtime Error
Syntax errors are identified when the user attempts to run the program. But the run-time errors are more troublesome. While they still result in the program not running to completions, they are intermittent – sometimes the program runs, but other times it does not.
There are many possible reasons for the runtime error. Perhaps there is a line the program in which the square root of a value is calculated. Most times the input to the square root is non-negative and the program calculates the square root and continues on to the end of the program. But there are some inputs that will result in a negative value being sent to the square root function. If the program does not address the imaginary value from the square root, it will crash the program.
To identify and correct the possible run-time errors you need check your code against many different inputs. Remember that the goal is to make the program fail. As such try inputs that might result in a divide by zero, or a negative square root, or create an infinite loop. These inputs may not exist in reality but as long as the program allows them there is possibility of run-times errors.
Logic Error
The main reason for testing is the logic error. Recall that a logic error is when everything runs but the results are just plain wrong. In this case there is no indication of a problem so the user will just take the information and run with it.
Black Swan Effect:
The black swan effect is described as some event that is so rare – or even impossible – so little attention is paid to it. Then when it happens it has a major impact on the system. It was described by economist Nassim Nicholas Taleb
The Black Swan Effect describes an event that is unexpected but then happens – often with severe consequences. It comes from the idea that since no one had ever seen a black swan, they therefore do not exist – but then suddenly one appears. It is a means of explaining the importance not ignoring events that have a low probability. It is a commonly discussed in finance and investing but can be just as important in engineering.
The approach to eliminating logic errors is to try many expected inputs. If the range of input values are fifty to one hundred try runs with input running the full range – all with the goal of trying to make your program crash. And remember the limits. If the normal range is fifty to one hundred but can be as low as zero or as high one thousand, check fifty and check one hundred. But also run your program with zero and one thousand. If the extreme inputs can happen they eventually will happen. Remember the Black Swan Effect.
But we also get into the nonsense. There is a saying in programming that you need to make your program idiot-proof. But remember that once you do, someone will invent a smarter idiot. This means that if you have every reasonable input covered there is still the chance that someone will enter unreasonable data. You need to test these values as well. If your program is well written then error checking the inputs will catch even the most ridiculous inputs.
Computing is the process of converting data in to information. Not a complex idea but one that defines a clear goal. Data are facts. But these facts are the basis behind making decisions. Decision making requires information. To transform data in to information we compute.
This process commonly follows a specific steps that must be done in a predetermined order – an algorithm. An algorithm is the process. With a single fixed starting point and a set of pre-determined steps it will perform this transformation. The magnitude of the number of steps that the algorithm needs is measured by its complexity. For a person the complexity must be small, constant or linear for most data. But computers can automate the process and enable us to perform millions of calculations a second. This opens up the computation to algorithms that operate in quadratic or more generally, polynomial time. But the growth rate of a non-polynomial time algorithm, such as those that run in exponential or factorial time, will be unusable on even the fastest computers for all but the smallest data sets.
The algorithm is more commonly known as a program regardless of whether or not it is run on a computer. But our goal is to automate the process and have a computer do the processing for us. This requires us to program the computer to perform the algorithm.
The process of writing the program can be approached in a manner similar to any engineering design process. We state the problem. We determine the requirements – in this case the inputs and the outputs. We prototype the solution, or in programming we work out a simple solution by hand. We build the product or system – we write the program. And finally we test, and test, and retest.
Testing a program is intended to identify two of the three types of errors. Errors can occur as syntax errors, runtime errors, and logic errors. Syntax errors, such as misspellings, or incorrect statements, will result in the program stopping at that point. It will never continue on past that. But runtime errors and logic errors are different and the reason it is so important to thoroughly test a program.
A runtime error will sometimes run but it may also crash at a point. Because it may be intermittent it is important to test a wide range of inputs. The more varied the inputs the more likely the runtime error will occur.
A logic error occurs when the program runs but returns incorrect results. The hand solution is always a good starting point in identifying logic errors, but it is just as important to test impossible inputs to confirm that impossible inputs do not result in what appears to be possible results.
Programming as a method of problem solving or decision making does not require a computer, using a computer to solve the problem is faster, can be used on models too large to be done by hand, can be repeatable without careless occurring, and is simply more fun.
But to program the computer will require a method for entering the program into the computer. For this we will need a programming language.
- Explain the differences between computer and computation.
- What is data? What is information? Give differences between them.
- What is an algorithm?
- An algorithm is a finite set of instructions that when followed will perform particular tasks.
- What is a basic schema of an algorithm?
- An algorithm must have a starting point
- All the steps must be deterministic
- It should have an end after a finite number of steps.
- Should account for any contingencies
- What is the difference between an algorithm and a program.
- An algorithm can be defined as a precise set of rules that describe how to solve a problem.
- A program is an ordered set of instructions that implement an algorithm.
- What is flow chart and why are they used? What are all the shapes used in a flowchart?
- Flowchart: It is schematic of an algorithm. It shows each step involved in the process with connections indicating the next action once a step is complete.
- Shapes in FlowChart: ellipse, trapezoid, rectangle, diamond/rhombus
- What are the different flowchart structures?
- 3 structures: Sequential structure, selection structure, repetition structure.
- Provide an example for sequential structures?
- Addition or subtraction of 2 numbers
- Write a flowchart for multiplication of two numbers using repetition structure.
- Use multiplication using the addition. For 5*4, add 5 repetitively 4 times.
- Why is complexity of an algorithm important?
- To compare algorithms based on the hardness of an algorithm, number of computational steps involved, space and memory used by the algorithm.
- Explain the different time complexities. What is the best and worst complexity for an algorithm. Illustrate a case where polynomial complexity can be considered worse than an exponential.
- Time Complexities:
- Constant time
- Logarithmic time
- Linear time
- Log-linear time
- Quadratic time
- Polynomial time
- Factorial time
- Exponential
- The best time complexity for an algorithm is constant time and worst is factorial or exponential.
- A polynomial can be better in following case:
- Consider a polynomial algorithm with complexity say: n3
- And an exponential algorithm say: 2n.
- Let say, the n value cannot exceed 8. In this case,2n < n3, for all n<=9. Thus, polynomial time worse than exponential in this case.
- Explain how a binary search has logarithmic time complexity.
- The binary search algorithm always divides the input into half, find the required data, again divides it into half and goes on till the input becomes a single element.
- The number of steps before the input becomes a single element will be (log2 n).
- How are exponential algorithm useful in secure password mechanisms?
- The exponential algorithm can be used to identify the number of combinations that one should try to crack a password of fixed length. This is used in the password mechanisms to make that set of combinations as huge as possible.
- What are steps involved in engineering design process
- Steps:
- Stating a problem
- Determining the inputs and outputs
- Writing the program
- Explain the ideal process of writing a program
- Program should be written in reverse order. We first return all the outputs, create fake input data and work on computations or analysis, then finally create the input data.
- What are the different programming errors? Explain briefly about each of them.
- Syntax Error: Most common error, mostly occurred due to misspelled commands and variables.
- Runtime Error: They may produce the results in the program but still not running to completion. They can occur due to several reasons and are hard to crack
- Logic Error: The program runs successfully and still gives the wrong answer. This is due to there is no syntax error or run time error but there is an error in the computation of the program that is not giving the expected results.

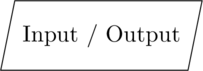


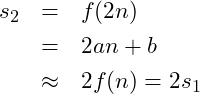
![Rendered by QuickLaTeX.com \[\hat{x} = \begin{cases} \frac{1}{2}\left(x_{\frac{n}{2}} + x_{\frac{n}{2}+1}\right) & n \mbox{ is even}\\ x_{\frac{n+1}{2}} & n \mbox{ is odd} \end{cases}\]](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-b3b19ffe9247caf0a3cc9ae51d8505ff_l3.png)
![]() .
.![]() . This is a common complexity for a single repetition structure or loop.
. This is a common complexity for a single repetition structure or loop.![Rendered by QuickLaTeX.com \[\bar{x} = \frac{\sum_{k = 1}^n x_k}{n}\]](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-100b07a5291b352ac64ac0386e2e7960_l3.png)
![]() time, is an example of a quadratic time algorithm.
time, is an example of a quadratic time algorithm.![]() cities with known distances between each city, what is the shortest possible route that a person can visit each city and return their starting point? The Traveling Salesman Problem – TSP – is a common example of a factorial time algorithm.
cities with known distances between each city, what is the shortest possible route that a person can visit each city and return their starting point? The Traveling Salesman Problem – TSP – is a common example of a factorial time algorithm.