5 Procedural Programming

A place for everything and everything in its place.

Reverend Charles Augustus Goodrich

\text{Many of us approach} programming in the same way we approached high school composition – despite everything our teachers told us.

We were told when writing a composition you begin by brainstorming your ideas. From there you create a basic outline of the main topics you would like to cover. You make this outline more detailed by adding subtopics and sub-subtopics. When you have the paper thoroughly outlined – and only then – you write the first draft – by hand. You edit and reedit the drafts until you are comfortable with the current draft. At that point – and not before – you start up the computer and begin typing the final copy.

What do we as programmers – as well as every first semester composition student – actually do? You have a paper to write so you open a new file on the computer and you start typing. You proofread it – mainly for spelling and typos – on the computer. You print it and turn it in.
How does this relate to programing? When we have a task that we think a computer program would be an effective problem-solving method we tend to start up the computer and start writing code. We do not plan the program. We simply start at the first line and work until the last line.
ow does this relate to programing? When we have a task in which we think a computer program would be an effective problem-solving method we tend to start up the computer and start writing code. We do not plan the program. We do not brainstorm or create flow charts. We simply start at the first line and work until the last line.
We can be much more effective and efficient in our coding if we plan out the program. But how do we plan a program?

Top-Down Design

Big Fleas have little fleas upon their backs that bite ’em. And little fleas have lesser fleas and so ad-infinitum.

Any task can be overwhelming when we only think of getting to the final result. But the reality is that all tasks actually consist of several smaller tasks each of which are more simple when addressed individually. An example is graduating from college.

As an example, every engineering student shares a common goal. To receive a degree in engineering. But how do we accomplish this?
Instead of thinking only of the final goal, break the task down into several smaller tasks. In this case graduating with degree in engineering can accomplished by successfully completing four tasks; successfully complete year one; successfully complete year two; successfully complete year three; and successfully complete year four.
The four subtasks do not explain how to perform the task just what has to be done. Instead we will select one and look at it in more depth – Successfully complete year two. And while you are in your second year there is no reason to be working on tasks that involve year three or year four.

Rendered by QuickLaTeX.com

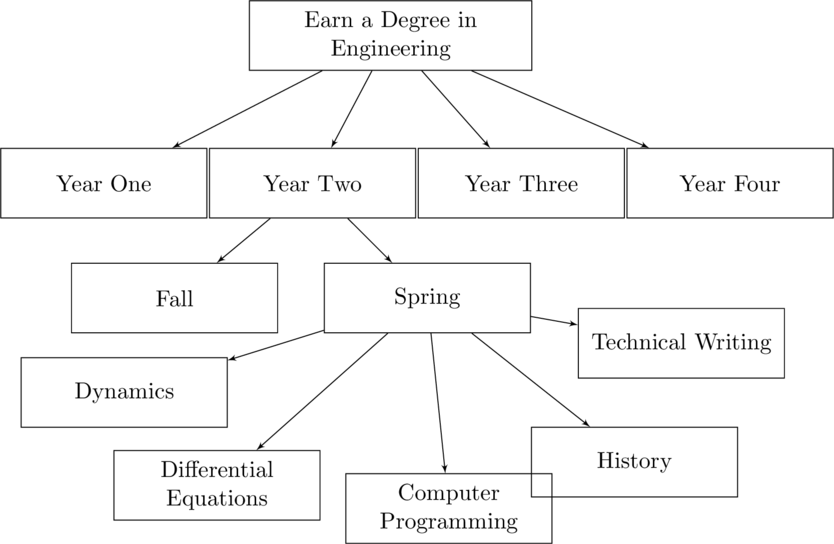
Hierarchical Chart for Earning an Engineering Degree.
Further, year two has a Fall and a Spring semester. If it is Spring you have five courses. At any single moment of the semester there is only one class for a particular course that we should be attending.

This is basis of top-down design; each task is broken down into the set of subtask that when combined complete the larger task. The subtasks are then broken down into the set of tasks that when completed will have completed the individual subtask. This is repeated until each item is trivial.

The diagram for earning an engineering degree in the figure is known as an hierarchical chart. It is a means of breaking down a task into all of its subtasks. It shows that while there may be a multitude of tasks that will have to be completed, at any single moment there is only one that is active at any given moment.

Top-down design provides a means to compartmentalize these processes so that we can plan what tasks will need to be done.

Hierarchical Chart

A means of planning the top-down design involves creating an hierarchical chart. The hierarchical chart is similar to a flow chart. But unlike a flow chart where the items show the sequence of steps that will be followed, the hierarchical chart lays out each task and its subtasks. It does not provide the order of running the tasks but instead it provides a means of planning identifying the tasks will have to be done.

Hierarchical Chart:

An hierarchical chart is a diagram in which each task is broken down into the smaller subtasks that comprise it.

Rendered by QuickLaTeX.com

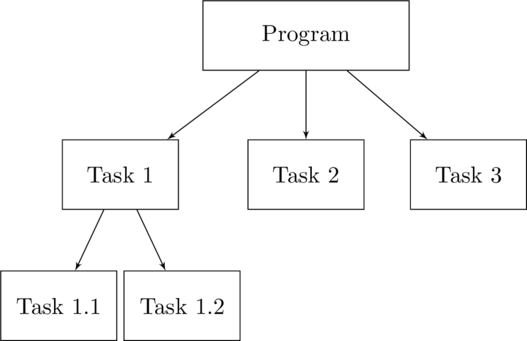
Hierarchical Chart for Top-Down Programming.

While an hierarchical chart can be beneficial for any problem management our interest is using it to implement top-down design to make programming an algorithm more efficient. In this application the tasks are functions.

Functions

While different programming languages call them by different names – such as methods, subroutines, or procedures – functions are the implementation of top-down design. Regardless of the name their purpose is the same. A function performs some specialized task in a program.
Function
A set of code that performs a particular task.

 

The purpose of functional programming or what is often called procedural programming, is that it enables us to use top-down design to simplify programming.
In a small way, we have already been writing functions in our programs. The program itself is a function. It performs all of the tasks that we want the program to perform. There is not much reason to think of a program as a single function, but to implement top-down design we will now need to so. Instead of the entire program in one function, we will now consider the lead, or main, function as a driver of the rest of the program. Our goal will to eliminate all of the details from this function and instead let it act as a project manager; calling each function when it is needed and doing only the most basic computing itself.
Named Function
An important aspect of the driver function in MatLab is that the name of the function is the same as the name of the script file. Thus we may also call it a named function.

 

This analogy of driver as project manager lends itself to a flow chart, figure Flow Chart for the Driver as Project Manager, of the program from the perspective of the driver. All that the driver does is call other functions.

Rendered by QuickLaTeX.com

Flow Chart for the Driver as Project Manager
Taking the executable details of the program away from the driver will provide additional benefits. A program will now consist of multiple functions that
  • can be divided between many members of a development team. Each member might be responsible for only one function but when all joined into the program will provide the needed functionality.
  • can be used multiple times. If a function only performs a single task, but that task is needed multiple times it only needs to be coded once.
  •  can be easily revised. It often occurs that a function will be have to be updated. When this occurs only a single portion fo the program will have to be changed.
  • can be more easily debugged. Since each function performs only a single task it will by its nature be a much smaller part of the program. If there is an error in it then the error is likely to be more easily found and corrected.
Function Calls and Definitions
It is important to differentiate between the function call and the function definition.
  • Function Call
    • To use a function you need to call it. The function call is a single line with the function handle, a set of of input variables, and a set of output variables
  • Function Definition
    • The function definition is the list of instructions or executable statements that are run when the function is called. For a local function it will start with the keyword function and finish with the keyword end.

 

The functions that we will be using can be separated into two types; built-in functions and user-defined functions.

Built-in Functions

Luckily for us there are a multitude of functions that are built into MatLab. We could not print without disp( … ) or fprintf( … ). We could not enter data into the program without input( … ). And without sqrt( … ) we would have to write our own code to calculate the square root of a number. These are examples of built-in functions.

Function call:

A function call is a program statement that passes control of the program over to a subprogram, or function. The function then performs a task and returns control to the point in the program from which the function was called.

Function Calls:

In MatLab, implementing a built-in function is done by making a function call as in the figure. The function call has three parts; the function name, the list of output variables, and the list of input parameters.

The output variable list and the input parameter list are optional. If the function does not return values to its driver function then there is no need for the output variables. Similarly, if the function does not require the driver to pass data to it for it to operate then > is no need for the input parameters. It is important that the parentheses be included even if the function does not require input data.

  1. % Syntax of a MatLab Function Call
  2. [output vars] = function_name(input vars);
Syntax of a Function Call
Built-in functions can be called directly from the command line in the same way that calculations can be done from the command line. The date( ) function does not require inputs or outputs so it can be called directly.
  1. >> date()
  3. ans = 24-May-2019
Calling the date( ) function from the command line

Computational functions will more often have both inputs and outputs.

  1. >> x = sqrt(42.0)
  2. x=
  3.        6.4807
  4. >>
Calling output variable = sqrt(input parameter) from the command line
s with simple calculations, function calls from the command line can be convenient but their value is in how they are run from a script.
  1. function driver( )
  2.      % DRIVER driver( ) is the main or driver function for the program
  4.      % Enter data
  5.      x = input('Enter the value for the square root: ');
  6.      s = sqrt(x);
  7. fprintf('sqrt(%0.3f) = %0.3f\n', x, s);
  9. end
  1. >> driver()
  3. Enter the value for the square root: 42
  4. sqrt(42.000) = 6.481
Calling output var = sqrt(input par) from a script

Built-in Functions

MatLab has built-in functions that address many calculations. The basic trigonometry functions are listed in the table.

Function Example Description
sin y = sin(radians) Sine of argument in radians
cos y = cos(radians) Cosine of argument in radians
tan y = tan(radians) Tangent of argument in radians
sind y = sind(degrees) Sine of argument in degrees
cosd y = cosd(degrees) Cosine of argument in degrees
tand y = tand(degrees) Tangent of argument in degrees
asin radians = asin(y) Inverse sine in radians
acos radians = acos(y) Inverse cosine in radians
atan radians = atan(y) Inverse tangent in radians
asind degrees = asind(y) Inverse sine in degrees
asind degrees = acosd(y) Inverse cosine in degrees
atand degrees = atand(y) Inverse tangent in radians
hypot c = hypot(a, b) Square root of the sum of squares (Pythagorean Theorem)
Table: Trigonometric Functions
There is also a set of general algebraic functions in the table. With the exception of the hypot function the input for each of these is a single value and each return a single value as well.
Function Example Description
exp y=exp(x) Base e exponential, y=ex
log y=log(x) Natural logarithm
log10 y=log10(x) Common logarithm (Base 10)
log2 y=log2(x) Base 2 logarithm
pow2 y=pow2(x) Base 2 power
sqrt y=sqrt(x) Square root
abs y=abs(x) Absolute value
Table: Algebraic Function

Overloaded Function:

An overloaded function is a function that while having a single function name performs different tasks depending upon the function signature.

But functions are often multivariate. The hypot function is an example. When called the program passes two values to the function representing the shorter two legs of a right triangle. The function calculates the length of the third side – the hypotenuse – and returns that value to the driver.
  1. function driver()
  2. % DRIVER driver( ) is the main or driver function
    for the program
  4.          % Enter data
  5.           x = input('Enter the first leg: ');
  6.           y = input('Enter the second leg: ');
  7.           z = hypot(a, b);
  8.           fprintf('The right triangle has sides %f, %f, and %f\n', x, y, z);
  10. end
  1.  >> driver()
  3. Enter the first leg: 4
  4. Enter the second leg: 3
  5. The right triangle has sides 4.000, 3.000, and 5.000

Passing two values to a multivariate function

It is possible for a function to return more than one value. The conversion functions in the table have several functions that return two and even three values.
Function Example Description
deg2rad d = deg2rad(r) Convert angle from degrees to radians
rad2deg r = rad2deg(d) Convert angle from radians to degrees
cart2pol [theta rho] = cart2pol(x, y) Transform Cartesian coordinates to polar or cylindrical – 2D
cart2pol [theta rho z] = cart2pol(x, y, z) Transform Cartesian coordinates to polar or cylindrical – 3D
cart2sph [azimuth elevation r] = cart2sph(x, y, z) T Transform Cartesian coordinates to spherical
pol2cart [x y] = pol2cart(theta rho) Transform polar or cylindrical coordinates to Cartesian – 2D
pol2cart [x y z] = pol2cart(theta rho, z) Transform polar or cylindrical coordinates to Cartesian – 3D
sph2cart [x, y, z] = sph2cart(azimuth, elevation, r) Transform spherical coordinates to Cartesian
Table: Conversion Function

There are two functions in the table that appear twice; cart2pol and pol2cart. These are overloaded functions; functions that have the same function name but depending upon the its function signature it does a different calculation or performs a different task. Each function has a unique signature consisting of the function name and the number of input parameters.

The number of output variables listed is the maximum number that can have values be returned from the function. It is possible to return fewer – or even zero – but the result may not be as expected. The function itself determines the number and type of values to return. It could be that a single variable in the output list could return a single value, or it could return a vector with multiple values, or could just result in a run time error.

 

Because of this, unless you know how the function will respond it is best to have the same number of variables as the function is designed to return.

Function Signature:

The function signature is a unique representation of the function call that indicates which function should be executed.

  1. function driver()
  2. % DRIVER driver( ) is the main or driver function  for the program
  3.      % Enter data
  4.       x = input('Enter the x coordinate: ');
  5.       y = input('Enter the y coordinate: ');
  7.       [theta, radius] = cart2pol(x, y);
  9.      fprintf('\t\t(x, y)\t\tradius\t\tangle (rad)\n');
  10.      fprintf('\t(%0.2f, %0.2f) %10.2f %10.2f\n)', x, y, theta, radius);
  12.  end
  1. >> driver()
  3. Enter the x coordinates: 4
  4. Enter the y coordinates: 3
  5. (x, y) radius angle(rad)
  6. (4.00, 3.00) 5.00 0.64

Returning different number of outputs values

While returning fewer values is useful, there is an issue. You cannot pick and choose which value to return. If you want the first only then you only need a single variable on the left of the assignment operator. But if you only want the second you must have two variables within the square brackets on the left. If you have only one – and even if you name with the second variable – it will receive the value in the first return variable.

Warning:

If you use fewer values than what is shown in the return variable list you may get unexpected results. Unless you know how it the function handles this it is best to provide variables for all of the return values.

Finding an appropriate built-in function

With the thousands of built-in functions that are available how do you 1. know what functions are available, and 2. know how to use the function?

MatLab provides you with many functions that are meant to be called from the command line, as compared to being coded into a script. Because of the way that they are commonly used these functions are usually given the moniker commands instead of functions. Two of these system command can help with finding and using built-in functions. They are lookfor and help.

lookfor:

lookfor is a system command that searches the function help files for a particular keyword.

Searching for a function

With the thousands of functions that are available how might you find the one that you need? lookfor is a system command for searching for a functions.

  1. % Syntax of the lookfor command
  2. >> lookfor keyword

Syntax of the lookfor command

Each built-in function contains a block of comments that are intended to provide help to the programming. The lookfor command functions by searching these help files for the keyword that you entered. If it finds the keyword then it returns the function name in which it was found and also a short description of the function (in the figure).

  1. >> lookfor cosine
  2. acosd       Compute the inverse cosine in degrees for each element of X.
  3. cosd        Compute the cosine for each element of X in degrees.
  4. acos        Compute the inverse cosine in radians for each element of X.
  5. acosh      Compute the inverse hyperbolic cosine for each element of X.
  6. cos          Compute the cosine for each element of X in radians.
  7. cosh       Compute the hyperbolic cosine for each element of X.
  8. >>

Example of the lookfor command

Help with a function

The lookfor command will provide you with a list of possible functions but it does not tell you how to implement the function in your script. What input parameters does it require? What are the outputs values? These can be found using the help command.

  1. % Syntax of the lookfor command
  2.  >> help function name

Syntax of help command

 

As an example, in the  figure shows the use of the help command for the exponential function, ex.
  1. >> help exp
  2.   exp Exponential.
  3.      exp(X) is the exponential of the elements of X, e to the X.
  4.      For complex Z = X+i*Y, exp(Z) = exp(X) * (COS(Y)+i*SIN(Y)).
  6.      See also expm1, log, log10, expm, expint.
  8.      Reference page exp
  9.      Other functions name exp

Example of the help command

The built-in functions are a feature of the top-down design in MatLab but there purpose is not so much to break tasks down.

 

Local Functions

“If you want it done right, do it yourself.”

-Napolean Bonaparte

Despite there being hundreds of built-in functions, and probably hundreds of thousands more that can be found in repositories, there is a need to be able to write your own.

Local Function:

A local function is a user defined function that is written outside of any other function. It can be called by any other function in the same script.

Top-down design demands that the program be broken down into a finite number of trivial tasks. These are not just tasks for which someone else has already written a function. These include specialized printing functions. Functions to perform inputs and error check those inputs. And most often, functions that simply perform some small set of calculations. It often makes sense to hide away the details of these functions and instead just use a function call.

Warning:

A common error in writing local functions is to embed them within another function. It is necessary that the entire local function, from the keyword function to the keyword end be completely outside of any other function. This includes the driver.

The most common type of the do-it-yourself function is a local function. This is a function whose function definition takes a form similar to that of the driver function. But the local function definition is written outside of the driver function or any other local function. Because of the importance of their being separate from all other functions, a common approach is to write each one after the current final keyword end of every other function.

A local function will have two parts; a function call and a function definition. The function definition is the set of executable statements for the function. It will take the same format as the driver function but must be completely outside of any other function.

Output Variables

The local function is very similar to the driver function that we have been using from the start. It begins with the keword function and concludes with the keyword end. On the first line, after the keyword function  on the left side of the assignment operator is the list of output variables. There does not have to be an output variable and there is no upper limit to the number used. If there is not a return variable then it, and the = are omitted. This is the usual case in the driver function. If there is more than one then they listed separated by either commas or a space within a pair of square brackets.

  1. [output vars] = function_name(input vars);
  2.       % Help comments for the local function
  3.  
  4.       % Operations for the local function
  5.  
  6. end
Syntax of a local function

Function Handle

Following the output variable list is the function name or what is known as the function handle.

Function Handle:

The function handle creates an association to the function. While it looks like variable name, the function handle is a structure that includes information about the function. This includes the function name,  the type of function, and the file in which the function is written.

The function handle is not a variable or simply a name but is in fact a structure. Each item in the structure contains information about the function including its name, type of function, and the file, if any, in which the function is written. This is information is available by calling a function called functions. You can do this from the command line as in lisiting.

structure = functions(@f):

The built-in function functions returns the details of the function handle that is passed to the function. This includes function name, the type of function – whether built-in, local (scoped), nested, or anonymous, the file in which the function is stored, and the parent function for the function.

The function handle makes is possible to pass a function to another function as in input (in Passing function handles to functions section). The naming convention for a function handle is the same as it is for variables.
  1. >> functions(function_handle)
  3.      function: 'function_handle'
  4.          type: 'scopedfunction'
  5.          file: 'functionsExample.m'
  6.     parentage: {'driver'}

Example of the functions command

Input Variables

The third, and final part of the first line of a local function is the input parameter list.
The input parameters are a comma delimited list of variables that will be receiving data from the driver. They are not, however, the variables from the driver. Instead they are new variables that are created when the function is called. They receive a copy of the value in the variables in the driver.

There is no lower or upper limit on the number of parameters. You may create local functions that have no variables, or hundreds of variables, or any number in between. The figure Example of a local function shows a local function with two input parameters.

Input Variables:

The input variables do not currently exist but will be created when the local function is called. The values in these variables are copies of the values in the variables in the function call.

  1. function driver( )
  2. % DRIVER driver( ) is the main or driver function for the program
  4. % Input data
  5.       x = 5;
  6.       y = 3;
  7.              % Call the local function
  8.       z = local_function(y, x);
  10.              % Print the Results
  11.       fprintf('f(%f, %f) = %f\n', x, y, z);
  13. end
  14. % All local functions are written outside the driver
  15. function r = local_function(base, power)
  16. % LOCAL_FUNCTION r = local_function(s) is an example of a local
  17. % function. Two values are passed in and one is returned 
  19.       %Calculate the value of r
  20.       r = base.^(power);
  22. end
  1. >> driver( )
  2. 3.000 .^ 5.000 = 243.000
  3. >>

Example of a local function

Comment:

It is not necessary that the variable names in the input parameter list be the same as the variables in the function call. It is often recommended that you provide different variable names for these variables to differentiate between the variable in the function call and the variable in the local function.

While most local functions are intended to perform specialized calculations, they are also used for customizing inputs and outputs. These include output functions; local functions that print results; and input functions or have the user enter data into the program.
Output functions are local functions that print. It could be printing descriptions as we will see in the print\_header function, or printing the results of calculations.
Input functions are the opposite. They enable the user to enter data into the program. This could be as simple as calling input or they could be designed to collect data from equipment, sensors, or network servers. Input functions will often include error checking to ensure the data being used in the program meets the proper criteria or constraints.

Output Functions

An output function is a type of local function that prints but does not actually return a value. A common example is a splash screen function (in the figure Example of a splash screen function).
  1. function driver( )
  2. % DRIVER driver( ) is the main or driver function for
  3. % the program
  5.      % Print the Splash Screen
  6.      print_header( );
  7. end
  8. % All local function definitions are written after the driver
  9. function  print_header( )
  10. % PRINT_HEADER print_header( ) prints start up information
  12.      %Print the splash screen
  13.      fprintf('\n');
  14.      fprintf('This is the Splash Screen \n');
  15.      fprintf('It acknowledges the programmer and provides\n');
  16.      fprintf('distraction while the program is loading\n');
  18. end
  1. >> driver()
  3. This is the Splash Screen
  4. It acknowledges the programmer provides
  5. distraction while the program is loading
  7. >>

Example of a splash screen function

This splash screen function does not receive any inputs or return outputs. It just prints. We can make a change to it so that it does receive a set of input parameters and then adjusts what it prints based upon the inputs. This is a form of customization that will make the function portable, that is generalized so that it can be used in many other programs without any changes. The items that do change are passed to the function instead of hard coded into it.
In this example, the figure Splash screen function with input parameters, the splash screen will print the programmer’s name, the date, and a short description of the program. If we copy this function into a different program, all that we need to do is change the date and description in the function call. The function definition does not change at all.
  1. function driver( )
  2. % DRIVER driver( ) is the main or driver function
  4. % Set the inputs to the splash screen
  5.      name = 'Joe Bfstk';
  6.      current_date = '28 May 2019'
  7.      desc = 'Showing off the Splash Screen';
  9.      % Print the Splash Screen
  10.      print_header(name, current_date, desc);
  11. end
  12. % All local functions are written after the driver
  13. function  print_header(n, d, description)
  14. % PRINT_HEADER print_header(n, d, desc) prints start up information
  16.      %Print the splash screen
  17.       fprintf('\n');
  18.       fprintf('Name: %s\n', n);
  19.       fprintf('Date: %s\n', d);
  20.       fprintf('Desc: %s\n', desc);
  21.      fprintf('\n');
  23. end
  1. >> driver()
  3. Name: Joe Bfstk
  4. Date: 28 May 2042
  5. Desc: Showing off the Splash Screen
  7. >>

Splash screen function with input parameters

In this customized version of print\_header the data is loaded into three variables in the driver. The values are then passed to the function where three new variables are created and the data from the driver is copied in to them.
This approach, writing a function that is passed data to be printed while not returning data to its driver is useful for printing results. By placing all of the output printing together it can be handled by a single function call while at the same time being formatted to make all of the output the most effective for the user.
  1. function driver( )
  2. % DRIVER driver( ) is the main or driver function
  4. % Enter data
  5.      dist = 400.0;
  6.      vol = 28.0;
  7.      % Calculate the fuel efficiency
  8.      lpk = 100.*vol ./ dist;
  9.      % Print the results
  10.     print_results(dist, vol, lpk);
  11. end
  12. % Local functions are written after the driver
  13. function  print_results(d, f, e)
  14. % PRINT_RESULTS print_results(dist, fuel, efficiency) prints a formatted table
  16.      %Print the results as a table
  17.      fprintf('\n');
  18.      fprintf('Distance: %13.1f km\n', d);
  19.      fprintf('Fuel: %17.1f liters\n', f);
  20.      fprintf('Efficiency: %12.2f liters/100 km\n', e);
  21.      fprintf('\n');
  22.  end
  1. >> driver( )
  3. Distance:        425.3 km
  4. Fuel:             29.7 liters
  5. Efficiency:        6.98 liters/100 km
  7. >>

Example of an output function.

With functions that perform calculations and functions that are meant to to print, all that is left is a function that is used for entering data into the program.

Abstraction:

Abstraction is the process of reducing the complex nature of a program into smaller, and hopefully simpler steps. It is done using top-down design and the use of functions.

Input Functions

A means of entering data into a program has already been provided with the built-in function input. This function prompts the user and then receives the user’s data entry, storing it in s variable. It differentiates between numerical data and strings of text. It is, however, limited.

The input only accepts user entered data – it stops the execution of the program and waits for the user to type on the keyboard. It also requires that each time a value is to be entered it a separate call to input must be made. What if there are multiple data values to be entered? Or if the data is being sent from an alternative device such as a sensor or server, or from a network feed?
If the data is to be user entered, input does not provide any error checking – an important part of any data entry but especially so for user entered data. .
An improvement to the input function is to create a wrapper function. This is a function that might combine multiple calls to input so several data values can be entered while at the same time moving the details out of the driver. Not limited to data entry, their use is to provide abstraction and thus programming convenience.

Wrapper Function:

A wrapper function is a function whose purpose is to call one or more other functions while performing a minimum of computation. It is a means of abstraction in that the implementation details are hidden from the outside.

The wrapper function can be used to combine multiple inputs into a single function while at the same time providing error checking all while keep the details out of the driver.

Adding in a wrapper function to the fuel mileage program is shown in the figure Example of an wrapper function.
  1. function driver( )
  2. %      DRIVER driver( ) is the main or driver function 
  3.      % Enter data 
  4.      distance = get_data('Distance driven: ');
  5.      volume = get_data('Fuel purchased: ');
  6.      % Call function to calculate efficiency
  7.      lpk = fuel_efficiency(distance, volume);
  8.      % Print the results
  9.      print_results(distance, volume, lpk);
  11. end
  12. % All local functions are written after the driver
  13. function x = get_data(prompt)
  14. % GET_DATA get_data(prompt) is a wrapper for input data
  16.      %Call the input function
  17.      x = input(prompt);
  18. end
  1. >> driver( )
  2. Distance (km): 400.0
  3. Fuel purchased (liters): 29.7
  5. Distance:        425.3 km
  6. Fuel:             29.7 liters
  7. Efficiency:        6.98 liters/100 km
  9. >>
Example of a wrapper function

As the example progressed we were able to remove details from the driver and replace them with simple function calls. By the end the driver did little more than just call other functions. All the details are handled in the local functions. This is the abstraction that was described earlier.

Local functions are are written outside of the driver function. This means that the function definition of a local function may not be within any other function. They are designed so they may be called from every other part of the program. This includes both the driver function – the function with the same name as the script file – and any other local function.

Nested Functions

There are programming applications in which applying abstraction suggests that you write a function, but the function has only a limited use. Perhaps it will only be used in a single function, or it requires input values that only exist within a function, or it uses parameters that must be defined before the function can even be defined. In these cases the use of a nested function can be useful.

Nested Function:

A function that is defined completely within another function is nested within that function. They are exist, and are thus callable, from within their parent function.

  1. function driver( )
  2. % DRIVER driver( ) is the main or driver function
  4.      % Enter data
  5.      r = input('Enter the radius of the polygon (m): ');
  6.      % Nested function to calculate area
  7.      function a = areaPolygon(n)
  8.      % Area of a regular polygon
  9.           a = (r.^2) .* n .* sind(360 ./ n) ./ 2.0;
  10.      end
  12.      % Print areas
  13.      fprintf('Triangle: %10.2f m^2\n', areaPolygon(3));
  14.      fprintf('Square: %14.4f m^2\n', areaPolygon(4));
  15.      fprintf('Pentagon: %10.2f m^2\n', areaPolygon(5));
  17. end
  1. >> driver( )
  2. Enter the radius of the polygon (m): 5
  4. Triangle:     32.48 m^2
  5. Square:       50.00 m^2
  6. Pentagon:     59.44 m^2
  7. >>
Example of a nested function
A primary difference between a nested function and a local function is how it uses variables. Any variable that is created in the parent of the nested function is available to the nested function. In a local function only those variables created within the function are available to the function.
This can be seen in the example in the figure Example of a nested function. The user enters the radius of the polygon in the driver. When they call the area function they pass the number of sides – but not the radius. The radius, being created before the nested function in the parent function, is automatically available to the nested function.
Because of the variable behavior we could write the nested function with no input variables at all. In fact, there are many times when this is done. The reason for the nested function is then a matter of repeatability. If there is a set of code that needs to be implemented multiple times, but only in a single function, then a nested function can greatly shorten the amount of coding that goes into the function.

Anonymous Functions

There is a third type of function, that while often confused with nested functions, it is more like a local function. But in reality. they are really neither. These are anonymous functions.

  1. function_handle = @(input parameters) expression;

Syntax of an anonymous function

An anonymous function is defined almost as if it were a single line expression. The difference is the addition of a declaration of a set of input parameters in the anonymous function.

Anonymous Function:

An anonymous function is a single executable line of code that is defined within another function.

Example

As an example, let’s recreate the area of the polygon function but this time using an anonymous function.
  1. function driver( )
  2. % DRIVER driver( ) is the main or driver function
  4.      % Enter data
  5.      r = input('Enter the radius of the polygon (m): ' );
  6.      % Anonymous function to calculate area
  7.      areaPolygon = @(n, r) (r.^2) .* n .* sind(360 ./ n) ./ 2.0;
  9.      % Print areas
  10.      fprintf('Triangle: %10.2f m^2\n', areaPolygon(3));
  11.      fprintf('Square: %14.4f m^2\n', areaPolygon(4));
  12.     fprintf('Pentagon: %10.2f m^2\n', areaPolygon(5));
  14. end
  1. >> driver( )
  2. Enter the radius of the polygon (m): 5
  4. Triangle:     32.48 m^2
  5. Square:       50.00 m^2
  6. Pentagon:     59.44 m^2
  7. >>

Example of an anonymous function

In this example, an anonymous function is defined within a parent function. Once done it is callable from that same function.
There is an important difference between the nested function example in the figure Examples of nested function and the anonymous function example in the figure example of an anonymous function. It is in the treatment of the two variables r – radius, and n – number of sides. In the anonymous function both the radius and number of sides need to be passed to the function as input parameters. But in the nested function the radius variable is not passed to the function but instead is inherited from the parent function. On the surface this appears to be a minor difference, but it is an important difference. The need to do this is the primary difference between the anonymous function and a nested function.

Anonymous functions or nested functions

Anonymous functions and nested functions share a couple of similarities. They are both defined within another function. Because of this they are only callable from the parent function or any nested or anonymous functions at the same level. An anonymous function cannot be called from other local functions in the program.

Anonymous or Nested:

There are similarities and differences between anonymous functions and nested functions.

Similarites

  • Defined within a parent function
  • Only callable from the parent or from other nested or anonymous functions at the same level.

 Differences

  • Nested functions inherit any variables and their values from the parent function.
  • Anonymous functions do not have access to variables in the parent function so the values must be passed to the function (encapsulation).
  • Anonymous functions can be parameterized, that is any variable that is not passed to the function in the input variable list is a parameter that is fixed for the lifetime of the anonymous function.
The difference is one that separates local functions from nested functions; encapsulation. Recall that a local function does not have access to variables in other functions while a nested function has a limited access to the variables that are declared in the parent function.
Variables in the parent function and variables in the anonymous functions are hidden from each other. In this way anonymous functions behave more like a local function. If you need data in an anonymous function then it must be passed to the function as an input parameter.
Similarly, any information that is created in the anonymous function must be returned to the calling function as the return variable. Since an anonymous function does not have an explicit return variable like local and nested functions, the return variable is the result of the anonymous function’s computation.

Parameters in Anonymous Functions

While an anonymous function does not have direct access to variables in its calling function, there is an exception. Any variable that is declared before the anonymous function can be used as a constant or a fixed parameter in the anonymous function. These parameters are fixed for the lifetime of the function..
  1. function driver( )

  2. % DRIVER driver( ) is the main or driver

    function
  3. % Enter data
  4.       a = input('Enter the first coefficient: ');
  5.      b = input('Enter the second coefficient: ' );
  6.      c = input('Enter the third coefficient: ' );
  7.      x = input('Enter the value of x: ' );
  8.      % Anonymous function to calculate quadratic
  9.      quadratic = @(x) a .* (x.^2)  + b .* x + c;
  11.      % Print value of quadratic function
  12.      fprintf('f(%0.2f) = %0.2f n', x, quadratic(x));
  14. end
  1. >> driver()
  2. Enter the first coefficient: 3
  3. Enter the second coefficient: -2
  4. Enter the third coefficient: 5
  5. Enter the value of x: 3
  7. f(3.00) = 26.00
  8. >>

Example of parameters in an anonymous function

Warning
Parameters in an anonymous function are fixed when the function is defined. While the variables in the calling function can be changed after the anonymous function is defined the parameters in the anonymous function will not.

In the example in the figure Example of fixed parameters in an anonymous function the parameters for the quadratic equation are set before the function was defined. Since they do not appear in the variable list for the anonymous function they are made to be fixed parameters. 

Once any parameters in an anonymous function are set they cannot be changed. You can change the variables that were used to create the anonymous function after the function was created but doing so will not change the function.

User entered anonymous functions

It often occurs in modeling that a mathematical function is not known when the program is being written. Or the function may change each time that the user runs the program. A solution is a user entered function.
A powerful use of anonymous functions is that instead of requiring they be hard coded – like a local function – into the program, they can be entered by the user at runtime.
Since strings of text can be entered at runtime, if the text can be transformed from a set of characters that form a mathematical expression into an anonymous function it can be called just like a function that was hard coded into the program. This is done with the str2func function.

f = str2func(s):

When entering a function as a string of text it is necessary to create a function handle for this function. This is performed with the built-in function strcat. The input to this function is a string of text, s. The output is a function handle, f.

Once the string expression has been transformed into a function it can be used like any other anonymous function. That is it can be called or passed to other functions.

Example

  1. function driver( )
  2. % DRIVER driver( ) is the main or driver function
  4. % Get the anonymous function
  5. f = getFunction( );
  6. % Enter the input value
  7. x = input('Enter the input value: ');
  9. % Evaluate the anonymous function
  10. y = f(x);
  12. % Print results
  13. fprintf('f(%0.2f) = %0.2f n', x, y);
  15. end
  16. function f = getFunction( )
  17. % GETFUNCTION getFunction( ) is a local function that
  18. % will allow the user to enter a string of text that can
  19. % then be used as an anonymous function
  21. %Enter the string
  22. s = input('Enter the function expression: ', 's');
  23. %Concatenate an @(x) on the front
  24. s = strcat('@(x)', s);
  25. %Transform s into a function handle
  26. f = str2func(s);
  28. end
  1. >> driver( )
  2. Enter the function expression: x.^2 - sin(x ./ 2)
  3. Enter the input value: 2
  5. f(2.00) = 3.16
  6. >>

String Concatenation:

String concatenation is the process of joining two strings together.

It is possible to write a function whose purpose is to have the user enter an expression that will become an anonymous function. In this approach the user enters a string of text. The text is then transformed into a function which is callable as any other anonymous function.
This function, f = getFunction( ), prompts the user for a string of text. It could have the user enter the input parameter list such as @(x), but in this case it is added to the front of the expression string.

After the input parameters are concatenated onto the expression, the final step is for the string to be transformed into a function handle. This is performed with the built-in function str2func(string).

The ability to have the user enter the function at run time can be quite useful. Imagine that you have a program in which you estimate the first derivative of a function at at particular point. The problem is that you do not what the function will be until you run the program.  It might be a quadratic, or a trig function, or something completely different. It would be useful to have the user enter the function after the program starts running and then it estimates the derivative of the function that was entered.

Passing Function Handles to Functions

The previous idea of estimating the derivative of a function can be abstracted by creating a local function that does the estimation. If the anonymous function could be passed to the derivative function.

Example

An example of passing a function to a function involves estimating the derivative. The person writing the code would not know what function needs to differentiated – if they did they would just solve it then.
  1. function driver( )
  2. % DRIVER driver( ) is the main or driver function
  4. % Get the anonymous function - use the function definition from before
  5.      f = get_function( );
  6.      %Enter the input value
  7.      x = input('Enter the tangent point: ');
  8.      
  9.      % Estimate the derivative
  10.      fPrime = derivative(f, x);
  12.      % Print results
  13.      fprintf('f''(%0.2f) = %0.2f n', x, fPrime);
  15. end
  16. function m = derivative(f, x)
  17. % DERIVATIVE m = derivative(f, x) is a local function that estimates the derivative of a function. This demonstrates passing a function to another function
  19.     dx = 0.01; % Small step size
  20.      m = (f(x + dx) - f(x)) ./ dx;
  22. end
  1. >> driver( )
  2. Enter the function expression: x.^2
  3. Enter the tangent point: 1
  5. f'(1.00) = 2.01
  6. >>

Estimating the derivative of a user entered function

 

Instead they can generalize the program so that the function can be created at run time, and then passed to the derivative function.
In the example (in figure Estimating the derivative of a user entered function) the user enters the function expression as text. The function handle along with a tangent point and a step size is passed to the derivative function. The derivative function uses the common formula for estimating the derivative of a continuous function at a point by calculating the slope of the secant line.

Scope and Lifetime

When a function, whether it be a local function or a nested function, or an anonymous function, a block of memory is reserved for the function. This includes space for any variables that are created in the function. When the function exits, returning any values to the calling function the memory is erased and with it the function and its variables. The availability of the function to the program is a matter of its scope and its lifetime.

Scope

In terms of functions and variables the scope is much like a person’s scope. For each of us, our scope is where we can be accessed; where can someone speak with us or call us or send us a message. We can control our scope by setting where we will be allowed to be contacted. Perhaps you will allow someone to meet with you or call you in your office, but not at home. Your scope is then your office. Another term for the scope is the visibility.

Scope:

The scope of a function or variable is the part of the program that can call or have access to the function or variable.

With respect to a function the scope of the function is from where in the program the function be called. This is often refined to which other functions may call it. There is a clear difference between the scope of a local function and the scope of a nested function.

Recall that a local function can be called from the program driver or from any other local function. Thus the scope is any other local function or the main program driver function.

But nested functions can only be called from their parent function or other nested functions that are at the same level in the parent function. The scope for a nested function is thus its parent function and other nested functions in the parent function at the same level.

Scope of variables

So how is this different for variables?

Variables created within a local function or within the driver function are, by default, only accessible within the function. Thus their scope is the function in which they are declared.

Variables in nested functions are treated a bit differently. Recall that variables created in a function are available to any nested function that was defined within the function. Because of this a variable that is created in a function, whether it be a driver function, local function, or nested function, adds to its scope any nested functions that are defined within it.

Lifetime

For a person, scope is where the person can be contacted or is visible to those who want to contact them. Their lifetime is when they become visible to the time that they are no longer visible; or birth to death.

Lifetime:

The lifetime of a function or a variable is when it is visible. It is normally the time from when the function is defined or the variable is declared until either the end of the function of the end of the program.

This is similar for functions and variables. Whereas scope is the visibility, that is where it is available in the program, lifetime is when. It is a chronological measure. Scope is where the function or variable is visible, lifetime is when it is visible

Lifetime of a function

For a local function the lifetime of the function is the from when the program begins to when it ends. For a nested function the lifetime is from when the parent function is called until it returns.

Lifetime of a variable

The lifetime of a variable is much like the lifetime of a nested functions. The default behavior of variables are that they are created when they are first declared – that is memory is reserved and normally a value is stored in memory for the variable, and are deleted when the function in which they are declared returns. Thus their lifetime is from when the variable is created until the function in which it is created returns control to the calling function.

If the variable is declared in a local function and the function in turn calls another local function, the lifetime of the variable continues but not the scope. This is a result of the function no longer being active, having passed control to the other local function. But if the function calls a nested function then the variable continues with both its lifetime and its scope since variables are accessible within the parent’s nested function.

Encapsulation

Encapsulation:

While normally a term applied to object oriented programming, encapsulation is a mechanism for restricting access to variables that are created in a function. It requires that all outside data that is needed in a function be passed to the function through the input parameters, and all information be returned to the driver function through a return variable. It is also known as information hiding.

Local functions and anonymous functions operate on the concept of ecapsulation. This means that all variables are by default hidden within the function in which they are created. Further, they are inaccessible from outside of the function unless they are explicitly passed to another function.

Encapsulation keeps all of the variables that were created outside of a function outside. It also keeps all variables that were created inside of the function inside. This is meant to provide stability. So how does this operate?
Imagine that yourself as a function. You sit in a locked room with only a single window. Nothing can get in and nothing can get out. Your job is to perform a calculation on three numbers that will be provided to you when your effort is needed. Until then you wait.
At some point during your time in the locked room three people come to the window. Each of them is holding a large flash card with a number on it. You do not know how they came up with the values, nor do you care. You write them down, in the order that they are presented, and get to work.
When you are done you write your result on another flash card. You take it the window and hold it up to the glass. Someone on the outside – you do not know whom nor do you know what they will do with the information – writes it down. You erase your four values – the three inputs and the one output – from your workspace and go back to waiting.

In this description, which may seem like a scene out of Tron, the function is completely isolated from the rest of the program. The function cannot access the outside variables. Instead the function must wait until the calling function provides it with the values in the variable. At no point can the function read or write to the outside variables. This is known as passing by value.

Pass By Value:

A parameter is passed by value when the calling function has a variable that contains data. At the same time the function being called creates a new, separate and independent, variable. The value in the calling function variable is then copied into the new function variable. If the function modifies its local variable, the change has no effect on the calling function variable.

Local Variables

When data is passed by value the variable that is created to accept the value of the calling function variable is a local variable. It is a new variable completely separate from the variable in the calling function. Instead of the original variable, it is a copy. Its scope and lifetime is determined by the function that is being called.

The new variable within the called function can have a different variable name than the variable in the calling function or it can have the same name. If you use the same variable name in the calling function as you do in the function that is being called, it is important to understand that there are now two separate variables with the same name but different scopes.

Note that the the variable x in the driver – whose value of 3 is passed to the function – is a different variable than the variable x that is created to accept the value from the calling function.

Local Variable:
A local variable is a non-global variable that is declared within a function. It has a scope and lifetime that are the same as the function in which it was created.
  1. function driver( )
  2. % DRIVER driver( ) is the main or driver function
  4.      % Enter data into the program
  5.      x = input( 'Enter a value for x: ');
  6.      %Call a local function
  7.       y = calculation_function(x);
  8.      % Print x and y
  9.       fprintf('Driver (x, y) = (%0.2f, %0.2f)\n', x, y);
  11. end
  12. function m = calculation_function(x)
  13. %    CALCULATION_FUNCTION m = calculation_function(x) is a local
  14. %    function that's purpose is to demonstrate that data that is
  15. %    passed by value creates separate variables
  16.      m = x.^2 - 3;
  17.      % Change x
  18.      x = x + 5;
  19.      % Print x and y
  20.      fprintf('Function (x, m) = (%0.2f, %0.2f)\n', x, m);
  22. end
  1. >> driver( )
  2. Enter a value for x: 3
  3. Function (x, m) = (8.00, 6.00)
  4. Driver (x, y) = (3.00, 6.00)
  6. >>

Demonstrating the separation of variables in pass by value

Warning:
When passing data to a function you may use the same or different variable names in the parameter list as you do in the function that has been called. Since they are two distinct variables that just happen to share a name, any changes to the variable in the function that was called will not be carried back to the variable in the calling function.

To avoid any confusion use a different variable name in the function from which the data is passed than the variable name in the parameter list of the function which is being called.

Since the default is that functions use encapsulation as a means to provide data integrity, is it possible to override this and change the scope of a variable multiple, non-nested, functions? It is and requires the creation of global variables.

Global Variables

The default of making variables local is important in supporting the goal of encapsulation. By keeping variables within their own function creates data integrity. A function that uses a variable that may have the same name as that in another function cannot change the value of the second variable.

Global Variables:

A global variable is a variable whose value is retained in memory after the function returns control. The value can then be shared by several functions. Its scope is all of the functions in which is declared as global. Its lifetime is the life of the program.

But there are instances when relaxing the control created by encapsulation can be useful.

You are writing a program to calculate deflections in a beam. Regardless of the loading on the beam the modulus of elasticity and the area moment of inertia will remain the same throughout the program. All of the functions that use these parameters are fixed and must remain the same for the run. But they may change the next time that the program is run. To guarantee that all of the functions use the same value for the parameters you would like to make the variables that store the parameters available to several different local functions.

The approach to the scenario described is to create global variables to handle the parameters. A global variable, also known as a static variable is created within a function by adding the modifier global in front of the variable name. By doing this the value of the variable is retained in memory after the function is done and has returned control to the calling function.
  1. global var
  2. var = value;

Syntax for Declaring a Global Variable

When using a global variable for the first time in a program you would have to set it to an initial value. But after that the value that is stored in memory will be used.
An example of using a global variable as a parameter in a set of local functions is shown in the Syntax for Declaring a Global Variable figure Using beam deflection calculations to demonstrate using a global variable as a parameter.
  1. function driver( )
  2. % DRIVER driver( ) is the main or driver function
  4. %     Create global variables
  5.      global E;
  6.      global I;
  7.      % Enter Dimensions and Load
  8.      a = input('Width of cross section (m): ');
  9.      L = input('Length of beam (m): ');
  10.      W = input('Load on beam (pounds): ');
  12.      % Set the parameters 
  13.      E = 29.0e06;% Modulus
  14.      I = a.^4 ./ 12;% Moment of Inertia
  16.      %maximum deflection
  17.      dPoint = deflectionCenterLoad(W, L);
  18.      dUniform = deflectionUnifLoad(W, L);
  19.      fprintf('\n Deflection of a Beam\n');
  20.      fprintf('Point Load: %10.2f in\n', dPoint);
  21.      fprintf('Uniform Load: %8.2f in\n', dUniform);
  22. end
  23. function d = deflectionCenterLoad(w, length)
  24. % DEFLECTIONCENTERLOAD d = deflectionCenterLoad(w, l)
  25. % calculates the center deflection of a beam with a center of the beam
  27.      % Global Parameters
  28.      global E;% Modulus
  29.      global I;% Moment of Inertia
  30.      % Deflection
  31.      d = w .* (length.^4) ./ (48 .* E .* I .* length);
  32. end
  33. function d = deflectionUnifLoad(w, length)
  34. % DEFLECTIONUNIFLOAD d = deflectionUnifLoad(w, length)
  35. % calculates the center deflection of a beam of length with
  36. % load spread uniformly across beam
  38.      % Global Parameters
  39.      global E;% Modulus
  40.      global I;% Moment of Inertia
  41.      w = W ./ length;
  42.      % Deflection
  43.     d = 5 .* w .* (length.^4) ./ (384.*E.*I);
  44. end
  1. >> driver( )
  2. Cross sectional width (m):
  3. Length of beam (m):
  4. Total load on beam (pounds):
  6. Center Deflection of a Beam
  7. Point Load:  m
  8. Uniform Load:  m
  9. >>

Using beam deflection calculations to demonstrate using a global variable as a parameter

In this example, the deflection of a beam is to be calculated. The deflection is determined in part by the modulus of elasticity, E, for the material and the area moment of inertial, I, for the shape of the beam. These two values remain the same for the different calculations as long as the beam remains the same. To ensure that the same value is used in each calculation they are made to be parameters and as such global variables.
The scope of a global variable is all of the functions which declare the variable as global. When a function that uses a global variable returns control the program cannot know if the variable will be needed again, so the value is retained in memory. As a result, the lifetime of a global variable is the lifetime of the entire program.
The retention of a global variable is one difference from a local variable. There is a second. A local variable must be initialized with a value before it can be used in an operation. A global variable does not. If a global variable is not initialized then it receives a default value of zero.
This provides a useful method for counting how often functions get called. You create a global variable counter in the different functions that you want to count the total function calls. Since you do not know which will be called first you simply declare the variable and it will be set to zero by default. Then in each function you add in increment to the variable.
  1. global counter; %  Set to zero the first time it is called
  2. counter = counter + 1;

Creating a global variable counter

Adding these two lines of code to a function will result in the variable counter being set to zero the first time that it is encountered regardless of the function in which it is declared. It will then immediately be incremented by one. Since the value is retained the value will increase by one each time any of the functions are called.

Summary

 

 

 

self test

License

Discover Computing Copyright © by Brian Adams. All Rights Reserved.