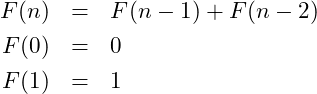Lather – Rinse – Repeat
Instructions on the back of a shampoo bottle
Recall that the purpose of a function is to simplify a program. Instead of having to rewrite code multiple times we simply write a function to perform some task for us. Then whenever we want that action we call the function.
There is a process that can be used in functions that allow a function to called from within itself. This process is known as recursion.
Recursion:
Recursion is a problem solving technique in which the solution is found by applying the same technique to smaller instances of the same problem.
Recursion provides a technique for repeating a function by having the function call itself.
While few of us have ever thought of it as such, recursion is how we run our lives. By performing the same tasks over and over again – not a specific number of times, but when we need to.
Think of walking out of a building. You do not say “I will take fifteen steps and then turn left.” No, you take one step towards your destination. If you are not at your destination you do it again – take a step towards your destination. You continue this until you arrive. This is recursion.
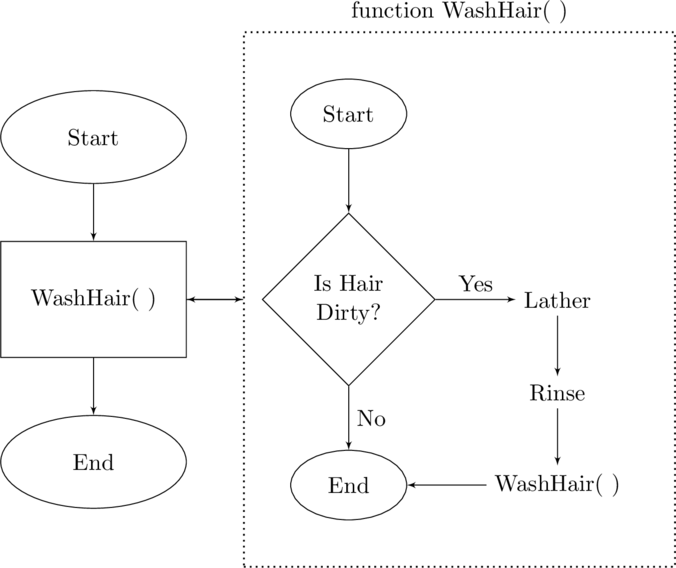
Another common example of recursion is the directions on a shampoo bottle – Lather – Rinse – Repeat. You can see this in the flow chart in the figure Flow Chart of a Recursive Function Call. While you might think of this as an example of a repetition structure it is open ended – something that was made for recursion. It does not say Do this twice: Lather – Rinse. Instead, it is actually a selection. It becomes so when we added the logical condition Does your hair need to be washed?
Flow Chart of a Recursive Function Call
Recursion is a combination of a selection in the form of either a simple if or an if-else and a function call. But the function call is what so often bothers us — it is a function call to the same function which is currently active. This is where the definition of recursion comes in — recursion is a technique that solves a problem by repeating the same solution on a smaller piece of the task.
We used an example from our daily routine to introduce the concept of recursion, but why use it in a program? Because just like the daily routine example solving problems with recursion is a natural method that we use to solve many problems.
Many recursive applications are computational. We will see examples for calculating factorials, and summations, and combinations. But others are not. Instead they perform a task, and if it is not completed — or completed incorrectly — then the recursive continues the process.
Examples of the non-computational use of recursion are often more direct. After all they are techniques that appear more natural because it might be how we would do the operation if we were not on the computer. The example that we will use to introduce the technique is error checking an input. But it can also be used for searching through data looking for a specific value or item, or it can be used to sort data — these last two will have to wait until we introduce vectors and lists. But error checking is a simple starting point for creating recursive functions.
Error Checking
Error checking is one of the most important processes in programming. The purpose is simple – counter the old saying of GIGO or Garbage In – Garbage Out. The recursive approach for error checking combines a means of entering the data into the program with the error check.
Error checking is also a natural recursive action. Imagine that you are at a deli counter. Your number gets called and you ask for a half pound of sliced cheddar. The deli clerk goes back and returns with a pound of provolone. They made an error, so you tell them that it is incorrect. Since the chances are that the clerk simply misheard you the first time, or became distracted, or simply forgot. Regardless, the most direct approach to remedy this is for you to ask for deli clerk for the cheddar again – textbook recursion!
function x = get_data_range(prompt, a, b)% GET_DATA_RANGE x = get_data_range(prompt, a, b) is a% recursive function that error checks the entered data. It% checks if the value is between a and b. If it is not then% it prints a warning and calls the get_data_range function% recursively.% The stopping condition uses a simple if, not an if - else.% % Enter the data using a call to input % with the string prompt x = input(prompt); % Create two logical variables to check range s = (x >= a); % These could be replaced with t = (x > b); % calls to the Heaviside function % Stopping condition % if it fails print warning and call get_data_range if(s.*(1-t) == 0) warning('%g outside of %0.3g to %0.3g', x,a,b); x = get_data_range(prompt, a, b); endend
MatLab code for Error Checking
This error checking function, in the figure MatLab code for Error Checking, does just this. It starts with printing a prompt to the user to enter the data. It then checks if it is within the specified range of values using the relational operator approach from chapter 7. This is known as the stopping condition or stopping case. If the check fails, the function prints a warning and then calls the function again. if the range check passes then the function returns the entered value to the calling function – the stopping, or base case.
warning:
Similar to error, MatLab has a function called warning that prints a message to the user, but instead of exiting the program it then allows it to continues.
Syntax:
warning(prompt);
This function could be adapted with other error checking in addition to – or instead of – the range of the input. You could check the type of value that was entered. For example that the value is an integer, or a boolean value. Or you could change the input to accept a string and then check that the text of the string contains a specific substring.
The important concept here is how the recursion worked. It is functionally similar to the error checking function that we created in chapter 7. But that function was a one off. The user was given the chance to enter the data. Once they did it error checked in the exact same way. But now if the user made a mistake in data entry it just warns them and lets them try again. Our first step into repetition.
Using recursion for calculations
Recursion as a tool for performing actions is valuable, but we also want to perform calculations. And recursive approaches to computation can at times be the difference between being able to complete a calculation or not.
The reason for a recursive approach is two fold. The first is that whatever the calculation is it is naturally recursive. We will see this in both the factorial calculation and the fibonacci series.
The second reason is that there are calculations that when written in their common form would overwhelm the constraints of the computer. This is the case in calculating combinations.
Factorials are a common calculation in combinatorics and in probability. The formula is well known
While many people would calculate the value starting at one, it is more direct to start at

just the way the formula is always presented. The reason is that this formula is naturally recursive.
The formula for
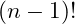
is
Substituting this into the original formula for the factorial results in the recursive form
(1) ![Rendered by QuickLaTeX.com \begin{eqnarray*}n! &=& n\cdot (n-1)\cdot (n-2) \cdots 2\cdot 1\nonumber\\ %n! &=& n\cdot \left [(n-1)\cdot (n-2) \cdots 2\cdot 1\right ]\nonumber\\ &=& n\cdot (n-1)! \end{eqnarray*}](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-c65e2e8d418fbedb32fe11ebf6ae47c6_l3.png)
A recursive approach to calculating
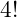
from the top down
(2) 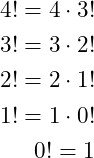
\noindent and then from the bottom back up
(3) 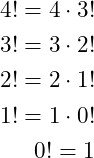
This recursive form is easily explained as the same calculation being done but on a different value. In other words, a factorial is actually the product of a single value and a different factorial.
Using this recursive approach if someone asks you what is four factorial, you answer “Easy – its four times three factorial!” And of course three factorial is three times two factorial. You just keep calling the factorial function on smaller and smaller values of

.
Of course you will need to stop at some point. You do this by recalling that
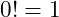
. Thus when you get to
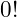
you replace it with the known value of

and start working back up through the calculations.
In this example knowing to stop at
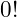
is called the
Stopping Condition or
Stopping Criteria while the value
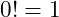
is the
Base Case.
The factorial function becomes a nature form of using this recursive formula. As such we can now write the formula as a function with which we can calculate any value of

as long as

is a non-negative integer.
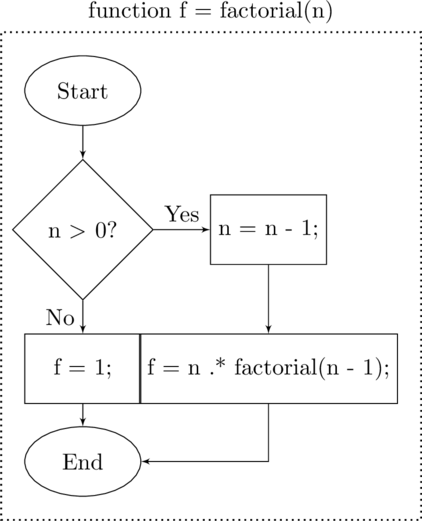
function f = factorial(n)
% FACTORIAL f = factorial(n) is a
% recursive function to calculate n!
% Check Stopping Condition
if(n >

)
%Recursive Call with Update
f = n .w* factorial(n-

);
else
Base Case
f =

;
end
end
Flow Chart and Matlab Code for a Recursive Factorial Function
While it may appear that recursion is repetition, it is actually a selection structure. The program calls a function. Within the function it evaluates whether or not some stopping condition is satisfied. Depending upon that result the function will either perform some operation(s) then call the function with an updated set of input parameters; or it sets a base case and returns control back to the driver. No repetition – just a selection in the form of an if – else structure.
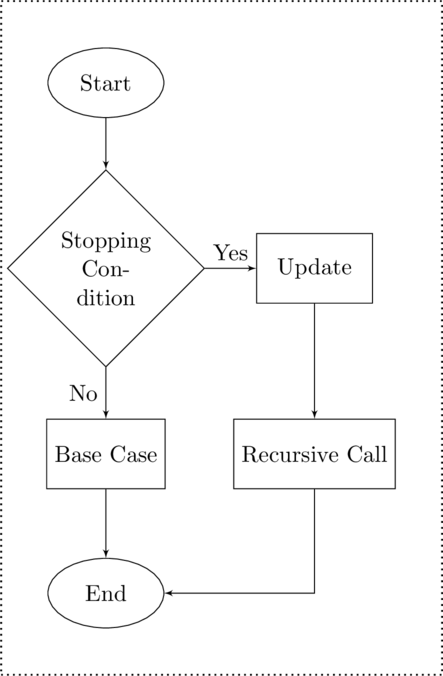
Three Rules of Recursion
A common question about recursion is “how do we know that it works?” The first thing to note is that recursion has a simple process – you call the function – the function makes an update to itself – the function then calls it itself. If we implement this correctly then it should work – but will it always work?
- This actually has a very simple answer. A recursive function will work as long as it satisfies the three rules of recursion.
- The base case must behave correctly.
- The stopping condition must result in a change in the inputs and move toward the base case.
- The stopping condition must call the function
Base Case
Base Case is the branch of the stopping condition that does not call the recursive function. The base case often returns a final value although it may also just return control of the function.
The flow chart in the figure Flow Chart for a General Recursive Function shows both the general form of a recursive function and the three rules.
Flow Chart for a General Recursive Function
While we will present it without proof, the three rules are both necessary and sufficient. This means that as long as our recursive function satisfies these criteria the recursion will work, and return the correct result.
Stack Memory
Recursive functions are a simple but powerful method for a program. Nevertheless there is a possible issue with their use – memory.
When a computer program runs the computer allocates a block of memory for the program. This memory is called the stack.
Each time that a function is called the stack stores the local variables for the function that are created. These variable remain in the stack as long as the variable is active. The stack operates as last in – first out (LIFO). This means that each time a function is called the memory needed for that function’s variables are pushed on to the top of the stack. When that function exits, that memory is released and returned to be used for the next function that is called. As long as a function is active the stack memory for other functions are not available.
LIFO:
LIFO is a queueing nomenclature for Last In – First Out. It indicates that when an item enters the stack it goes on the top pushing all others down. It will also be the first one to be popped or removed from the stack.
An analogy of the stack is to imagine a function is a sheet of paper. Each time that a function is called a new sheet of paper is added – pushed – onto the top of the pile – stack – making the other sheets of paper unavailable. As long as the function is active all memory activities take place on that top piece of paper. When function returns control the sheet of paper is removed and the paper – memory -below it moves to the top and becomes active.
An analogy of the stack is to imagine the tray carts that are used in cafeterias. Each time that a tray is put onto the cart is pushed onto the top of the stack of other trays making the other trays are unavailable. When that top tray is removed – freed from the stack – the tray (memory) below it becomes active.
Stack Overflow:
Stack overflow occurs when a function is called after all of the memory available for the stack has been allocated. It is a type of run-time error.
In recursion, each time that the function calls itself an additional block of memory is allocated for the function. While not normally an issue, the memory available for the stack is finite. This means that if the recursive function continues to call itself many times it is possible to allocate all of the memory that has been reserved for the stack. If so the next time that the function is called there will not be memory available for it and the program will crash. This is a type of run-time error known as a stack overflow error.
Stack overflow is commonly a result of infinite recursion. A misnomer because the function has not called itself an infinite number of times, but it is does occur when the recursive function as called itself so many times that there is no longer any memory remaining in the stack.
The most common reason for infinite recursion is an incorrect stopping condition. For example, if the function should update as long as
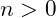
but the update adds one to

instead of subtracting the stopping case will never be reached. Eventually all of the memory in the stack will be allocated and the stack overflow error will occur.
Direct and Indirect Recursion
Using recursion to calculate the factorial is an example of direct recursion. Within the recursive function the same function is called again. But what if the recursive function calls another function which in turn calls the original function? This is still recursion but it is no longer direct, but is now indirect.
Recall that the factorial function calls itself recursively (figure Flow Chart and Matlab Code for a Recursive Factorial Function). This is direct recursion. So how would this change for indirect recursion?
In indirect recursion the recursive function calls a different function which in turn calls the original function. This makes it appear that individually neither function is a recursive function – but when viewed together it is.
Indirect Recursion:
Indirect recursion is when the recursive function calls a different function which in turn calls the recursive function.
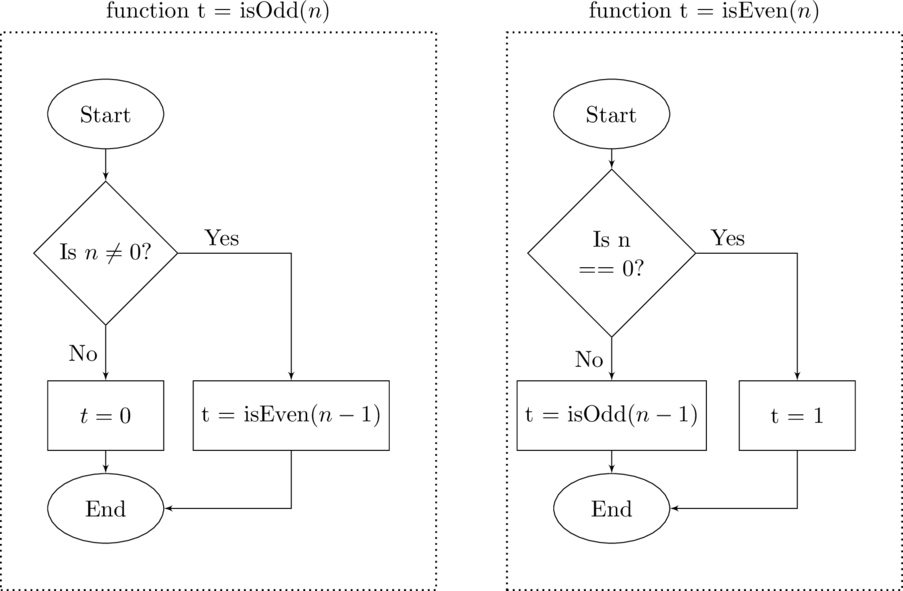
An interesting example of this is the indirect recursive function to determine if a number is even or odd. In this example the function first checks to see if the entered value is zero. Since zero is not odd it will by default return

for false.
Flowchart demonstrating indirect recursion
If the value is not zero it then moves the
isEven function for
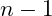
. If the value of

was originally equal to one then the new value is

and the function returns

for true – the current value is even and thus the original value was odd.
As before, the benefit of the recursive function is its simplicity in coding. Figure : MatLab code for indirect recursion shows the indirect recursion as MatLab code. If you had only seen one of these functions you would not have been able to identify it as a recursive function, but by looking at both together you should recognize that it is recursive and an example of indirect recursion as well.
Complexity
As we have with all implementations we are interested in the computational complexity of recursive functions. While most recursive applications are simple and fast
, it is possible to have a recursive algorithm that is beyond the acceptable complexity levels. The issue can be determined by whether the function implements single recursion or multiple recursion.
Single Recursion
function f = isEven(n)
% ISEVEN t =
isEven(n)
% determines if n is
even
% Stopping Condition
% 0 is not even nor
odd
if(n == 0)
% Base Case
t = 1;
else
% Recursive Call
% with Update
t = isOdd(n-1);
end
end
MatLab code for indirect recursion
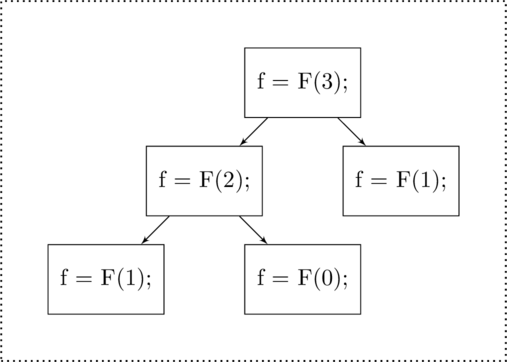
Single recursion is just what it says. The recursive function – either direct or indirect – makes a single recursive function call. Each example that we have already seen is an example of single recursion. The complexity of single recursion can be determined in a function tree for the recursive factorial function as shown in figure
Hierarchical diagram of single recursion. This example of single recursion is
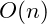
.
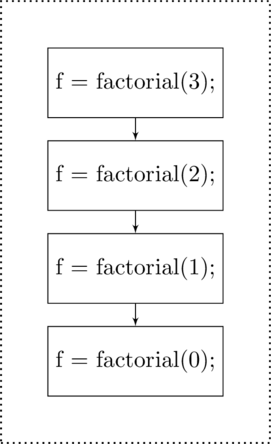
Hierarchical diagram of single recursion
While adjusting the input by subtraction is commonly
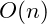
, it is possible to have a single recursive function that is better than that. An example code is shown in figure
Hierarchical diagram of single recursion. In this example the update is divided by two each time
Multiple Recursion
Multiple recursion is different. In multiple recursion the function makes more than one recursive function call each time. An example of multiple recursion is calculating the Fibonacci sequence.
The fibonacci sequence goes back to the thirteenth century. It is a sequence that is commonly found in nature. Its definition is recursive – each value is determined by the sum of the two values that come right before it.
Fibonacci:
Fibonacci was a thirteenth century mathematician from the Republic of Pisa. Also known as Leonardo of Pisa he is often thought to be the most influential western mathematician of the middle ages. He most often remembered for the sequence named after him.
(4) 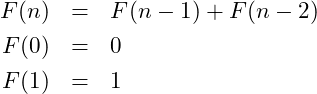
The sequence in equation~
4 is clearly recursive. Each term is calculated by adding the two that come before it. To calculate the sequence
The The hierarchical diagram in figure Hierarchical diagram of multiple recursion
shows that the
Hierarchical diagram of multiple recursion
Recursion can be used anytime that it is necessary to repeat a process. After all, recursion is a type of repetition structure. We will see that there are additional repetitions structures which we will call loops, There are actually programming languages that do not have loops but rely solely on recursion. While MatLab is not one of them, it is often possible to use recursion instead of a loop when a repetition is necessary.
There are many useful applications for recursion. They range from functions that perform computations to those that provide support to other actions. We already looked at error checking an input, but there are also applications in searching and sorting data.
Computation
When it comes to computation, many recursive functions are designed to simplify some repetitive operation. We have already seen the example of calculating a factorial. Recall that by its definition it is a recursive function, but we will see that it can be calculated using a loop, A similar example is the calculation of permutations and combinations. But the loop approach to these calculations has a different problem — the magnitude of the numbers. As a result, recursion becomes a necessity.
Both permutations and combinations belong to a class of functions used in
combinatorics. Combinatoric calculations are a basis of theoretical probability. As mentioned, the two primary combinatoric calculations are permutations and combinations. Each of them determines the number of selections that can be made from a set of

items when you are picking
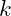
at a time.
The number of permutations of

items selected
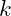
at a time is the number of ordered sets of
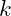
that can be formed from the

.
(5) 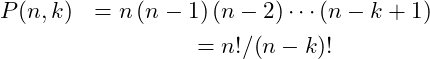
Combinations are similar to permutations, but the selected subsets are not ordered (the order does not matter). It is calculated by first calculating the permutations and then removing all the repeated selections.
The calculation is product and quotient of factorials.
(6) 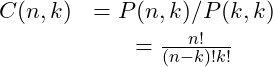
Permutations can be calculated using two factorials and combinations with three. The three factorials would at first make this appear to be an example of multiple recursion. But if you wrote the function using the three factorial functions it would actually works out to be singular recursion three times. As such it would still have complexity of
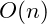
. But programming the function in this form is still not recommended. The issue is the magnitude of the calculations. To show this, try to calculate
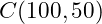
using factorials.
The alternative is to simplify the calculation to a single recursive function. But how?
Calculating combinations and permutations have been done for hundreds of years. When doing this by hand the factorial approach is untenable. But if you write out the factorial form you may see a simplification; one of the factors in the denominator will always cancel out. To see this try
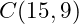
When you look at this calculation, what may jump out at you is the recursive nature of it. It is nearly the same as the factorial calculation. By grouping we see a new relationship
The sample shows how to identify the recursive relationship. We can generalize it to
(7) 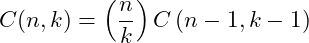
Writing the recursive relationship for combinations as a function is shown in figure MatLab code for Calculating Combinations.
function c = comb(n, k) % COMB c = comb(n, k) is a recursive function that calculates % the number of combinations of n items taken k at a time % % Check if k > 0 if(k > 0) % Update c = (n ./ k) .* comb(n-1, k-1); else % Base Case c = 1; endend
MatLab code for Calculating Combinations
![]()
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}n! &=& n\cdot (n-1)\cdot (n-2) \cdots 2\cdot 1\nonumber\\ %n! &=& n\cdot \left [(n-1)\cdot (n-2) \cdots 2\cdot 1\right ]\nonumber\\ &=& n\cdot (n-1)! \end{eqnarray*}](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-c65e2e8d418fbedb32fe11ebf6ae47c6_l3.png)
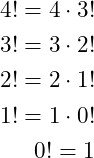
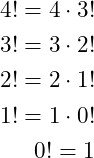
![]() is not odd
is not odd![]() =
= ![]() )
)![]() );
);![]() ;
;
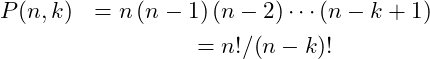
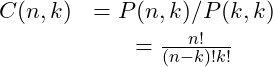
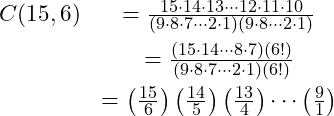
![Rendered by QuickLaTeX.com \begin{eqnarray*} C(15,9) &= \left(\frac{15}{6}\right)\left[\left(\frac{14}{5}\right)\left(\frac{13}{4}\right)\cdots\left(\frac{10}{1}\right)\right]\\ &= \left(\frac{15}{6}\right)\left(C\left(14, 5\right)\right) \end{eqnarray*}](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-f607067c51d3566f6e992a7b9c7e74cf_l3.png)
![]()