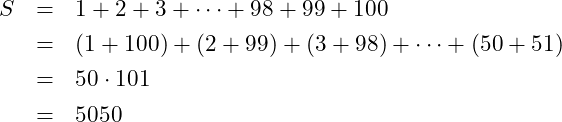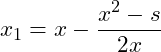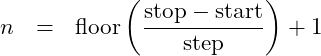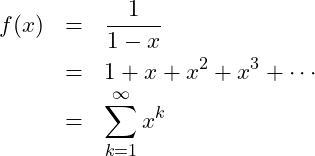There is a construct in computer programming called ‘the infinite loop’ which enables a computer to do what no other physical machine can do – to operate in perpetuity without tiring. In the same way it doesn’t know exhaustion, it doesn’t know when it’s wrong and it can keep doing the wrong thing over and over without tiring.
-John Maeda – American Designer
– no pun intended – in many fields. Some literary examples are
“Let it snow, Let it snow, Let it snow.” – Sammy Cahn
“Miles to go before I sleep, and miles to go before I sleep.” – Robert Frost
“But I would walk 500 miles
And I would walk 500 more
Just to be the man who walked a thousand miles
To fall down at your door” – The Proclaimers
Repetition Structure
A repetition structure is a block of instructions that are repeated sequentially as long as some condition is met.
In literature repetition is the act of repeating the same line a set number of times or until some other action causes it to stop. But how does this apply to computation?
I worked with a man who once told me “a computer does not do anything that any of us cannot also do. It just does it over and over without complaining.” This is repetition.
Repetition in a program is the act of repeating a block code either a fixed number of times, or until some condition is met, or once for each item in some predetermined list. The first two are examples of convergence, while the third is better known as iteration.
Loop:
A loop is a sequence of instructions in a program that can be executed repetitively either a fixed number of times or until certain conditions are satisfied.
Repetition structures are more commonly known as loops. In their most basic form a loop is a block of code that once begun will potentially run multiple times exclusive of the rest of the program. Each time that the block of code runs is known as a pass.
An historical example of repetition is actually a story of avoiding repetition.
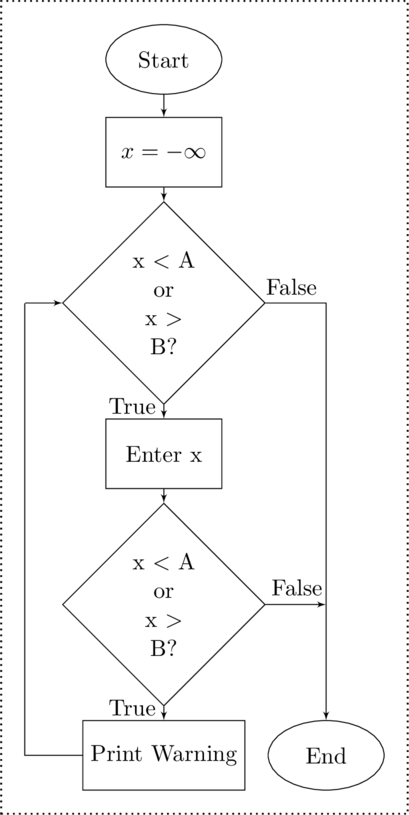
The story – perhaps apocryphal – is of a nine year old Karl Friedrich Gauss. A version of this is that his teacher as punishment to an unruly class directed the students in the class to add the numbers from one to one hundred most likely assuming that the task would take the class at at least an hour.
While the class worked away on the exercise, Karl simply sat idle for a few minutes, then picked up his pencil and wrote a number on his paper, and put the pencil back down.
The teacher was indignant at the impertinence of the student ignoring his assignment so he picked up the paper and saw the answer written on it — 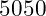 .
.
When confronted with his insolence, Gauss pointed out that he was able to simplify the task of repeated addition with a simple product.
(1) 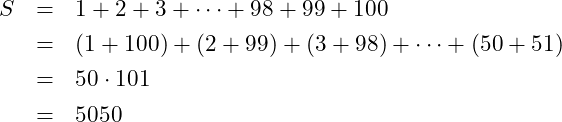
In this case Gauss was able to simplify a repetitive process in a way that was not obvious at the start. Instead of requiring a hundred passes through a loop, he was able to do it in two steps – a single addition followed by multiplication.
The Gauss example is a mathematical example of avoiding repetition. Using repetition Gauss would have started with

. Added
to it, then
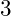
and so on until he had reached
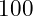
. The repetition was not in the values but in the process. He repeated the same process of adding a value to the sum until some goal had been reached.
Repetition structures – loops – come in two types; convergence loops and iterative loops. What is the difference between the two and how are they the same?
A convergence loop is one in which the number of passes is not known at the outset. Instead it will run as long as some logical condition is true. In a common type of convergence loop a set of calculations are repeated ending with a test or error calculation being made. The program continues to make passes through the loop with each pass having a value get closer to the correct result. The difference between the calculated value and the correct value would be the error. The repetition block would stop when this error drops below some acceptable value. It is unlikely that you would know the number of passes that the loop will need to make before the acceptable error is achieved so instead it runs until the calculated value converges to the acceptable value. Thus a convergence loop.
Convergence Loop:
The more common form of repetition is the convergence loop. It is a type of repetition structure in which a block of code is repeated until some condition is met. The number of passes that the loop makes might be determined prior to the start of the loop – such as in a counting loop – but it is also common that it is not known until the loop is complete.
A non-computing example of a convergence loop is a little leaguer trying to throw a baseball into a trash barrel ten meters away. He will continue throwing the ball towards the barrel until he gets one in. Once he does, he stops. He might get it on the first throw or the one hundredth. No one knows how many throws he will need to make – or in the programming vernacular – how many passes the loop will require until he actually makes it.
Another example of convergence is simple counting. It is not uncommon that we need to repeat a block of code five time, or ten times, or perhaps even ten million times. The number of passes through the block of code is not relevant. What is important is that the number of passes through the loop is know before the loop starts. It is still convergence because the loop repeats until some counter value is met – in effect until the counter converges to the predetermined value.
An example of this type of repetition is providing directions. A driver pulls over and asks you for directions. You point them in the correct direction and tell them to go through five traffic lights and then turn right at the sixth. The driver leaves and when they get to the first light they count one and continue driver (another pass through the loop). They repeat this for light two, three, four, and so on. If you were asked for the directions by other drivers you would always tell them the same number of traffic lights. In this second example the convergence is that you repeat until you have completed some task a fixed number of times.
In both of the examples, the loop will need to make some type of test to determine if the goal has been met – or at least is it close enough? A question that will arise is should the test be made before the first pass through the loop , or after the loop has run the first time? Which is the difference between a pre-test loop and a post-test loop.
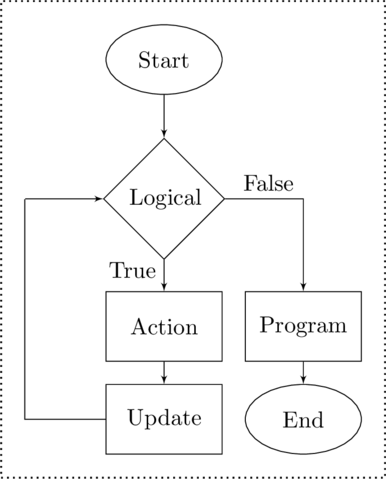
Pre-Test Loop
The pre-test loop is more colloquially known as the
while loop. It operates by first checking a logical condition. If the logical condition is
true – or

– then it makes a pass through the block of code that follows it. Once the pass is complete it returns to the logical test and the process repeats. In effect, the loop will continue
while the logical condition is true – thus the name
while loop. Eventually the logical condition will have to be
false – or

– when this happens the program skips the block and continues on with the program. The syntax of the
while loop is very similar to that of the simple
if selection structure. This syntax is shown in figure
Flow Chart and MatLab Syntax of a Pre-Test Loop.
Pre-Test Loop:
A pre-test loop is a repetition structure in which a logical decision is made before the loop begins. If it is true then the block of code is run. But if it is false the block of code is skipped and the program continues not having run the loop at all.
while(logical) % Code to run if the % logical is true % Updateend
Flow Chart and MatLab Syntax of a Pre-Test Loop
An important component of the while loop is the update. Each time that the program makes a pass through the block of code that forms the loop there must be the possibility that the logical condition becomes false. If it did not then the loop would never stop and we would have the run-time error known as an infinite loop.
To ensure that the loop does eventually end there must always be an update within the block of code. This can be an increment to a counter, or a check on error term, or any of many other means of having the logical condition change state from true to false. The method of the update is not as important as the understanding that it must exist within the while loop’s block of code.
Although the while loop can be used for either a convergence process or an iterative one. it is the ideal structure when we want the process to converge. The introductory example of throwing a baseball was an example of repetition until convergence is achieved, but we are not writing a program about throwing a baseball – although we could.
Example
Calculating a square root.
A technique that can be used to estimate a square root involves the Newton-Raphson Methos. In it, a starting value is guessed for the square root of
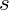
. We can use the value
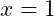
. If
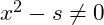
then
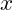
it is not the square root and we calculate a new estimate using ~
2.
(2) 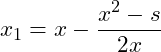
The convergence criteria is that
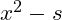
be zero which would mean that
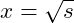
. So how do we code this using a convergence series?
function [x] = square_root(s, eps)% SQUARE_ROOT [s] = square_root(x, eps)% estimates the square root of the% value x using the Newton-Raphson% method % Error check the inputs if((s < 0) | (eps <= 0)) error('Error on input: out of range'); end % Set a starting value (a guess) for % the square root x = 1.0; % Enter loop - make passes till it % converges while(abs(x.^2 - s) > eps) % Calculate next term % This is also the update term x = x - (x.^2 - s) ./ (2.*x); endend
>> [s] = square_root(2, 0.001)s = 1.4142
Flow Chart and Code Sample of a Function to Estimate the Square Root of a Value
Take note that when the function is implemented it first check if the starting value is in fact the square root – or at least within some small distance from it. If it is, for example if the value of the square that is passed to the function were
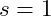
then the value
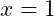
would be the square root and the loop would never run – or need to since it already has the square root.
The while loop in the example demonstrates the pre-test loop. Before any steps in the loop are run a test is made. In this case the test is if the starting value when squared is close to the value that was passed to the function. If the test is true – the value is far from the squared value – the code in the loop block is run. But if it were close then the test would have been false and the block would have never run.
Assuming that the test result is true the block runs, performs its calculations, may update some test value, and then returns to the logical test. This process will continue until the test eventually returns false and the algorithm ends. This characteristic of the pre-test loop can be described as test – run – repeat.
The test is the beginning creates an important consideration in the pre-test loop. Since the logical test is always done first, if it is false on the first test the loop would never run. That the loop might never run is an important design consideration in using a pre-test loop.
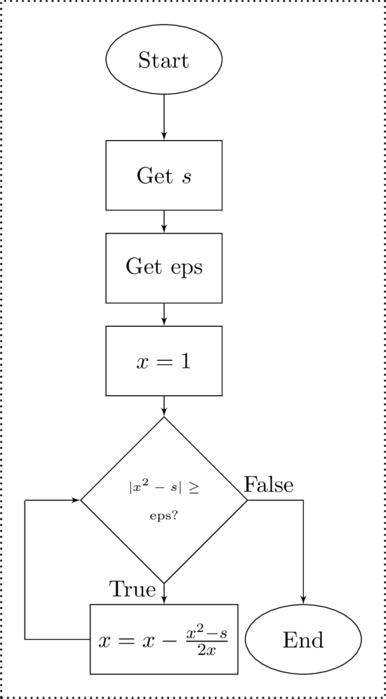
An alternative to this is to design a repetition structure that will always run at least one time. This type of repetition structure is known as a Post-Test Loop.
Post-Test Loop
Post-Test Loop:
A post-test loop is a repetition structure in which a logical decision is made after the pass through the loop. If it is true then the block of code is run again. If it is false the structure ends and the program continues. The post-test loop will always run at least one time.
The pre-test loops is just what is says – the loop performs a test before the loop begins. The result of the test determines if the program should make a pass through the loop or not. If the test is true – the pass is made. If it is false the loop block is skipped and the program continues. So how is this different from a post-test loop?
The sole difference is that the post-test loop makes a pass through the block of code and then it performs the logical test to determine if it should do it again. The main functional difference is that while a pre-test loop may not run at all, a post-test loop will always make at least one pass through the block of code that forms the loop.
The post-test loop is shown schematically in the flow chart of the post-test loop in figure Flow Chart of a Post-Test Loop with and adaptation of a while loop to mimic the Post-Test Loop, but MatLab does not have a post-test structure. So how would you implement this? You would adapt a while loop to function as a post-test loop. This does not imply that there is a post-test structure, but just that it can be mimiced by adapting something else.
You when you look at the syntax it shows another while loop – a pre-test loop. This is because MatLab does not implement a direct post-test loop. Thus you would have to adapt the while loop.
% Statement to force logical% to be truetest = 1;while(test) % Code to run if the % logical is true % Update % The update will need a % test = 0; at some point % in the loopend
Flow Chart of a Post-Test Loop with and adaptation of a while loop to mimic the Post-Test Loop
Since the only convergence loop available in MatLab is the while loop, you will need to adapt it to act as a post-test loop. This requires that you force the logical test to be true the first time that it is encountered. A common way of doing this is to set an initial value for the variable that will be updated in the block of the loop. As an example, if the logical test is that the loop should run as long as the value stored in the variable
x is greater than 10, then you set an initial value of
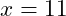
, or some value that is greater than
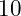
. Doing this will ensure that the loop always runs the first time that it is encountered.
Example
Note:
We could have made the initial value positive infinity just as easily as we did negative infinity, but it is more common for an input to have a lower bound while being unbounded above than it is to be unbounded below while having no upper bound, so this will usually be the better choice. An alternative is to use a flag that is initially set to true, then if the entered value is within the range the flag would be set to false.
Earlier, we had developed an error checking function by using recursion. An alternative method is to use a post-test loop. The reason for the post-test loop is that the block of the loop will contain the input function for the user to enter data. As a result the block of the loop must always run at least once or there would be no way for the user to enter data.
function [x] = get_data_range(prompt, m, M)% GET_DATA_RANGE [X]=get_data_range(prompt,% m, M)% has the user enter a floating point value,% then error checks that it is within the% range of m to M. If it is not it prints a% warning and starts again.%% This is a forced post-test loop % Set x to force the loop to run x = -inf; % Enter loop - will be true on first test while((x < m) || x > M)) % enter x using the prompt x = input(prompt); % test if out of range if((x < m) || x > M)) % print warning warning('Value out of range'); end endend
>> x = get_data_range('Enter value from 0 to 10: ', 0, 10)Enter value from 0 to 10: 50Value out of rangeEnter value from 0 to 10:
Flow Chart and Code Sample of a Function for entering data and then error checking it to ensure that it is within a pre-determined range
Because we do not have an actual post-test loop, this function will still require the use of a while loop – a pre-test loop. We adapt this by adding an initial value that will always result in the first test of the logical condition returning true. This is a common way to force a pre-test loop to act as a post-test loop.
The flow chart, figure : Flow Chart and Code Sample of a Function for entering data and then error checking it to ensure that it is within a pre-determined range, shows this initial condition to be negative infinity – a clearly small and out of range value.
When the user calls this function they would pass three variables; a string that will be the prompt, the lower bound, and the upper bound. The first pass through the loop – which will always happen – prompts the user to enter a value. It then uses a simple if selection structure to test if the value entered is out of the range. If it is the warning function is called printing a message to the user, and the pass ends and the flow returns to the test logical test. Since the value is already out of the designated range, the logical test simply repeats this and it will of course be true and another pass will be made through the loop.
Note:
We had earlier written a function in which we check the entered value to be sure that it is within a set range. At that time, in chapter Recursion, we used recursion. The recursive approach does not require the two sets of tests each time, or setting the initial value to force the loop. You could argue that the simplicity of the recursive function makes it a preferred choice.
When the user does enter an acceptable value – whether it is the first time or the fifteenth – the simple if test will be false and the warning will be skipped. The logical test within the while statement will also be false and the loop will end.
Convergence loops can function either pre-test or post-test. Regardless they follow the same algorithm – passes are made through a block of code until something result forces the loop to end. This could be a value for a counter or a sum is reached, or a mathematical operation gets within an acceptable distance from a value. But there is another possible type of repetition in which the program makes a pass through a block of code one time for each item in a list. This is known as iteration and the loop is an iterative loop.
There are many examples where a task is repeated once for each item in a set or list. In this case the the number of times that the pass through the block of code is known before the loop begins. while similar to a counting loop, this is different in that there are a specific set of items or elements in a list that well be accessed with each pass. This type of repetition is known as iteration.
Iterative Loop:
An iterative loop is a repetition structure in which a set or list of items is first created. The iterator is then set to each item in sequence making a pass through the loop for each one.
For Loop
For Loops
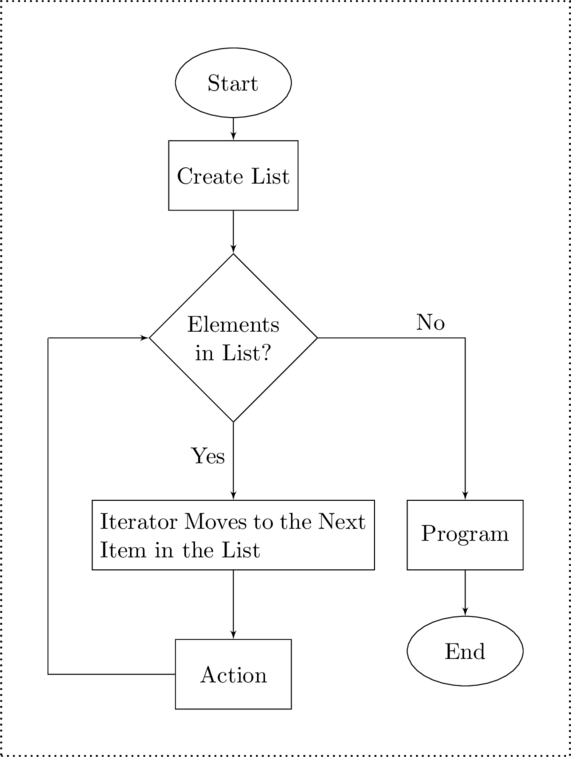
In MatLab the iterative loop is known as the for loop. It operates by creating a list of elements. It then steps or iterates though each item in the list. With each pass through the loop a variable – known as the iterator – is assigned the current element in the list. After the iterator has been assigned each element the for loop exits. The syntax of the for loop is shown in figure Flow Chart and MatLab Syntax of a For Loop.
- for k = [list]
- % In the for loop, k is an
- % an iterator. It is
- % assigned a single value
- % from the list one
- % element at a time
- % in the order in which
- % they are presented.
- % The action is the code
- % that is run in the block
- % of the loop. It will
- % continue to run as long
- % as there are items still
- % in the list
- end
Flow Chart and MatLab Syntax of a For Loop
The iteration is done automatically by the interpreter. So while the flowchart in figure Flow Chart and MatLab Syntax of a For Loop shows a step for having the iterator move to the next element you do not actually program this. Instead the for loop is structured as only the single line of code at the beginning of the block of code.
The MatLab implementation of the for is reasonably basic. It has only two components – the iterator and the list.
Iterator
In a for loop, the iterator is a variable that points to a single element in a set or list of elements. When the for loop is first created the iterator is assigned the first element in the list. At the completion of each pass through the for loop the iterator moves – or points – to the next element. This continues until the iterator has pointed to each element. It is because of its role in pointing to the current element of the list that the iterator in a for loop is also called a pointer
For our purposes the iterator in the for loop looks like a variable and acts like a variable, but is actually much more. While it retains the value of the current element in the list – a variable – it also maintains the location in the list – a pointer. While this is important, for us we still use it as if it were a variable.
List
The second component in the for loop is the list of elements. This can be called by several different names, list, array, vector, or simply set. In MatLab is often compared directly to a vector, but much the difference between an iterator and a variable, there are differences between a list in a for loop and a vector.
The list is the set of elements that will be assigned as a value of the iterator each time that it makes a pass through the loop. The list can be created in several different ways, but in its most common form the list is created by enumeration inside a set of square brackets, [ and ].
If you have a specific set of values of which you would like to assign to each pass through the loop then you create a list consisting of the elements. When part of a for loop, the list and the iterator take the form
k = [e_1, e_2, e_3, e_4, ... , e_5]
Creating a list using enumeration
where e_k is some numerical value or a character. The elements may be comma delimited or simply space delimited. Note that when this is used in a for loop, while it appears to be similar to an assignment statement it is not, Thus it should not have a semicolon at the end.
An example of using enumeration to create the list of elements in a for loop is in figure : Example of a for loop using enumeration.
fprintf('k = ');for k = [6, 2, 7, 8, 5, 2] % Statements to be run with each pass fprintf('%d ', k);end
Example of a for loop using enumeration
This approach to creating the list is known as enumeration. It is a useful technique when the number of elements is small or the elements that need to be accessed are not ins numerical order.
Enumeration:
Enumeration is the process creating an ordered collection of all the items in a list.
The elements enumerated in a list are not limited to numerical values. They can also be characters.
fprintf('k = ');for k = ['c', 'r', 'w', 'a', 'n', 's'] % Statements to be run with each pass fprintf('%c ', k);end
Example of a for loop a list of characters
An interesting result will occur if the elements are strings of text. In MatLab a string is already a list of characters. This results in the elements being individual characters instead of the strings.
In the sample code, each character of the two strings is interpreted as an element. This for loop would thus make ten passes through the loop instead of two.
fprintf('k = ');for k = ['Hello', 'World']% Statements to be run with each passfprintf('%c ', k);end
Example of a for loop with strings
Enumeration does have a downfall – size. Hardcoding a handful of elements in to a list is not a major undertaking. But for loop with hundreds, or thousands, or even millions of elements is not uncommon.
If the elements are ordered, then an alternative to enumeration is to create the list of elements as a range of values. The list will begin at a fixed starting value, and increase up (or decrease down) to a stopping value with each additional element increasing (or decreasing) by a fixed amount – the step size – from the previous value.
Creating a list using a range of values
There are several conditions that are applied when creating a list by range;
- The step parameter is optional. If it is omitted it defaults to

fprintf('k = ');for k = [5:12] fprintf('%d ', k);end
List example with step = 1
This creates a problem if the stop value is smaller than start. Since the default value for step is one, the list would consist of all of the elements from start decreasing to stop but with the difference between them being a positive number. This is impossible so the list will be empty. It will still be created, and the program will run, but since the list is empty there are no values for the iterator. No elements means that the loop will never run.
If the goal was to not create an empty list, you must explicitly set the step size. In this example the step is set to
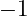
so that the iterator will decrease by one with each pass.
fprintf('k = ');for k = [9:-1:3] fprintf('%d ', k);end
List example with step = -1
2. The step size will determine the distance between each element. If the step is positive then the elements increase while if the step is negative the elements decrease.
fprintf('k = ');for k = [2:5:27] fprintf('%d ', k);end
List example showing the effect of the step value
If the step contradicts the order of start and stop, i.e., [8:2:-3], the list will be created but it will be empty. As with the missing step size, a for loop using this list will be created and the program will run, but the loop itself will not make any passes.
fprintf('k = ');for k = [18:3:0] fprintf('%d ', k);end
List example showing the list will not pass the stop value
3. The list will always terminate at the value at or below stop. Thus if the the range of values beginning at start and increasing by step does not include the exact value of stop then the terminal value will below the selected stop value.
fprintf('k = ');for k = [2:3:12] fprintf('%d ', k);end
List example where the list will stop short of the stop value
There is no requirement that the start, step, or stop values be integers. They can be assigned any value.
fprintf('k = ');for k = [0.9:3.7:8.5] fprintf('%d ', k);end
List example with non-integer values
Since the loop is designed to iterate through a fixed set of values the Gaussian sum is best implemented by using a for loop. But this is not the only implementation. We could also have written this code using a while loop.
It is possible to replace every for loop with a while. The challenge would be to replace the list of elements with a logical test and an update. This could be done by first determining the number of passes that the loop would need to make.
Calculating Number of Passes and Step Size
If you need to know how many passes a for loop makes, you can add a counter that updates within the loop. But it is important to be able to know how many passes a for loop will make before it is run. If the elements in the list were enumerated then you already know. But if you are using the range approach then number of elements is not so obvious.
The number of steps that is made is simply the integer value of the distance from the lowest value to the largest value divided by the step size. But there is one more element than there are steps – the first and last element bookend the list. Thus
(3) 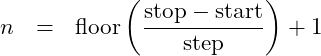
This equation will return the number of elements of a list where the start, stop, and step are known. It often occurs that you want the list to contain

elements equally spaced from start to stop. The equation in
3 can thus be solved for the step size.
(4) 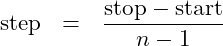
Using equation~
4 you can create a for loop with

elements equally spaced from start to stop by
k = [start:(stop – start)./(n-1):stop]
Creating a list a fixed number of elements
The approach in figure Creating a list a fixed number of elements is common enough that MatLab provides a function that does the heavy lifting for us. It is the linspace function.
linspace:
linspace creates a list of

elements equally spaced from start to stop
syntax: k = linspace(start, stop, n)
k = linspace(start, stop, n)
Creating a list a fixed number of elements
Repetition is the process is repeating a set of operations until some criteria is met – either a value converges, or perhaps a flag becomes false, or a list of elements is exhausted. The operations themselves are as varied as the applications of the loop. There is, however, an application of repetition that is so common that it warrants its own presentation; maintaining a running sum or total. In this application a variable is initialized before the loop, and then with each pass the results of a calculation are added – or subtracted, or multiplied, or divided – from the variable.
Accumulator:
An accumulator is a variable that is initialized before the implementation of a repetition structure and is then updated with each pass through the loop.
This variable is known as an accumulator. It is a variable that is initialized before the onset of a loop. Once the loop begins the value in the accumulator will be updated by the results of some operation that took place in the loop. In its more common use the accumulator is a counter. It keeps a running count of the number of passes that have been made through the loop.
But counters are not the only application of accumulators. They can be used for any application in which a running total, or sum, or product, needs to be maintained. While a single accumulator is often included with a loop, it is not uncommon for a loop to have multiple accumulators. This is often the case when you need to keep not just the count of the number of passes through the loop but sum of the operations.
An application of an accumulator as a sum is the calculation of the Taylor Series expansion of a function.
Example
Recall from the Calculus that the Taylor Series is an infinite series that converges to some value of a function on a particular interval. A common example is the geometric series, equation~5.
(5) 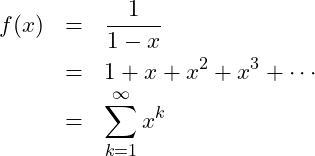
This series converges as long as

.
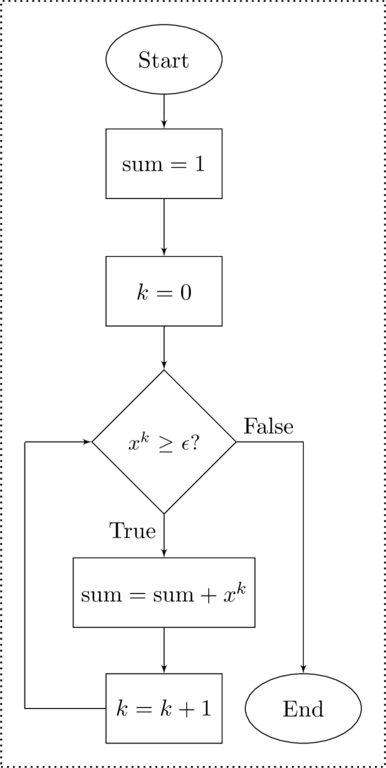
The series itself is infinite, but a sum of a finite number of terms of the infinite series will approximate the Taylor expansion. In writing code to do this approximation, there will be three items to address: How we do keep track of the current power of the term? How do we store the sum? And how many passes through a loop will be needed?
For the first we will create an accumulator to be the counter. This will be created outside of the loop and initialized to

.
For the second item, since it is a finite sum, we can create another accumulator to store the running sum. But this accumulator will be initialized to

before the first run of the loop. This is so that the first term of the series – which will always be

– when calculated outside of the loop will be compared to epsilon and will most likely be true so that the loop will run.
As to the number of passes – since the sequence is decreasing (remember that

thus a fraction so each term is smaller than the one before it) we should continue until the amount that the sum increase by the additional term is below our cutoff. This just means to continue until the next term to be added is below some value that is passed to the function by the user – an epsilon.
We could use a for loop if the user knows how many passes will need to be made before the loop starts. In this case we would create a list
![Rendered by QuickLaTeX.com k = [0:n]](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-40d0907094adb548329e98909439e157_l3.png)
. But that would be inefficient. Why make more passes than are needed. Instead, since we do not know the number of passes that will need to be made, we should use a convergence loop. This is shown in figure
Flow Chart and Code Sample of a Function to Calculate the Taylor Expansion of the Geometric Series.
function [s e] = geometric(x, eps)% GEOMETRIC [s e] = geometric(x, err) estimates% the geometric series using the convergence of% an infinite series % Error check inputs if((abs(x) >= 1) | eps <= 0) error('Error on input: out of range'); end % Initialize the accumulator, and counter sum = 0.0; k = 0; % Enter loop - make passes till converges while(x.^k > eps) % Calculate next term and add % it to the accumulator sum = sum + x.^k; % Update the counter k = k + 1; endend
>> [s e] = geom(0.5, 0.01)s = 1.9922e = 0.0078
Flow Chart and Code Sample of a Function to Calculate the Taylor Expansion of the Geometric Series
The Taylor expansion of the geometric function can be adapted to any continuous function. All that it takes is to change the terms of the sequence.
The convergence and iterative loops developed have all been single loops. This means that there is only a single repetition structure and a single set of passes. This works if, for example, a counter,
, needs to go from one to

. After making

passes it finishes and continues on with the program.
Imagine a second example – analyzing each point on a plane. This would require performing calculations over a two dimensional space – each
coordinate.
To do this you would have the program would start a corner – say
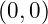
. The step through each
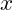
value until it reaches its maximum. At this point you have the program move
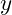
from

to

and then reset
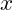
back to

. From here the process repeats. This continues until the value of
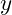
reaches it maximum value.
Each value of
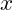
will require a loop and also each value of
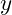
. But the
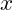
loop must run
for each value of
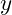
. This will require that the
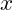
loop be embedded – or
nested inside of the
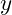
loop.
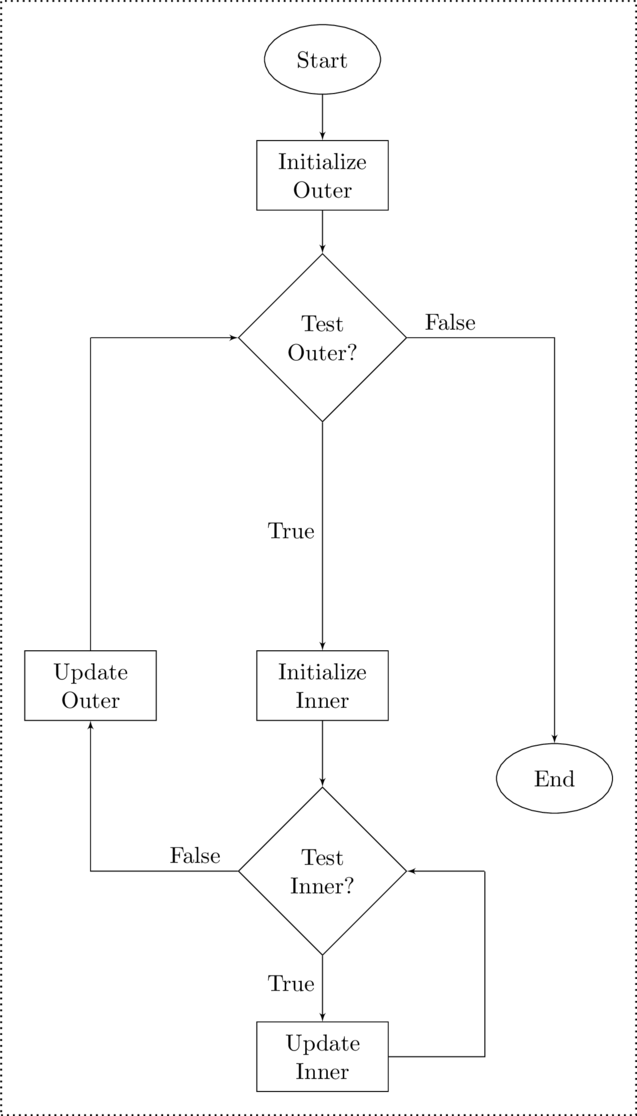
A flow chart to show the process of nested loops is shown in figure: Flow Chart of a Nested Loop. When the repetition structure is entered, any needed initializations for the outer loop will be made. A logical test for the outer loop is now made. If it is true then the inner loop is entered.
The inner loop is almost the same as the outer loop. Any initializations for the inner loop variables are made, and then the inner loop logical test is done. If it is true then a pass through the inner loop is made. In the inner pass, any updates that will eventually effect the inner logical test will be made.
Flow Chart of a Nested Loop
There are no restrictions on the types of loops that can be nested. A while loop can be nested within another while loop. A for loop can be nested within a while loop or vice versa. For loops can be nested within for loops. The for loop inside of a for loop is a common implementation of nested loops for working over a Cartesian plane – it is the example that introduced nested loops in this section.
An example of a function that implements a for loop nested within another for loop is shown in figure
Sample Function of Nested For Loops. In this example the function steps through each possible integer value of
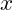
, then updates
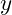
, and repeats stepping through
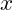
again. This continues until every
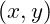
pair on the plane has been accessed.
function cart_plane(x_min, y_min, x_max, y_max, x_step, y_step) % Check nargin for number of variables if(nargin == 0) % Set start, stop, and step to default values x_min = 0; y_min = 0; x_max = 100; y_max = 100; x_step = 1.0; y_step = 1.0; elseif(nargin == 4) % Start and stop are passed to the function % Set step to default of 1.0 x_step = 1.0; y_step = 1.0; else error('Incorrect number of input parameters to function cart_plane'); end % Start the outer loop for y = [y_min:y_step:y_max] % Any operations for outer loop only % This is commonly empty but not always for x = [x_min:x_step:x_max] % All operations to be done the the point (x, y) end endend
Sample Function of Nested For Loops
There is no fixed limit to how deep the nesting of repetition structures can be. Two loops – an inner loop nested within an outer loop is common. As are having three loops nested one inside of a second inside of the outer, or third, loop. This example is one in which you might be accessing each coordinate point in a three dimensional space.
Nesting loops can be an effective means of performing multiple calculations without have to rewrite code. Simply have the same operations performed with each pass through the loop. The issue – if there is one – is that of time.
If a program makes

passes through a loop, where

is the number of pieces of data, then as we have seen before this algorithm would be
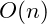
, that is it would have linear complexity.
If you nest two loops and the inner makes

passes while the outer loop makes
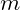
, then there would be a total of
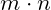
passes made. This would be a quadratic time algorithm,
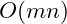
or more commonly
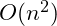
.
Continuing with this, three nested loops would be expected to be
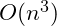
, while four is
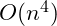
. If we extend this to
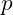
loops nested one inside of another it is
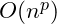
. All of these are still polynomial time algorithms and should not be of great concern. But if the number of passes is large – and millions is not unusual – the time requirements could be noticeable and perhaps severe.
As such, while repetition is a common technique in programming, if it is possible to eliminate a loop then it should be done. An example of this is the Gaussian sum that we used to introduce this chapter.
Example
The Gaussian sum is an application that uses a single pass repetition structure. Because it involves adding all of the integers from a starting value 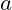 to a maximum value
to a maximum value 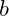 , it is a common implemented using a for loop.
, it is a common implemented using a for loop.
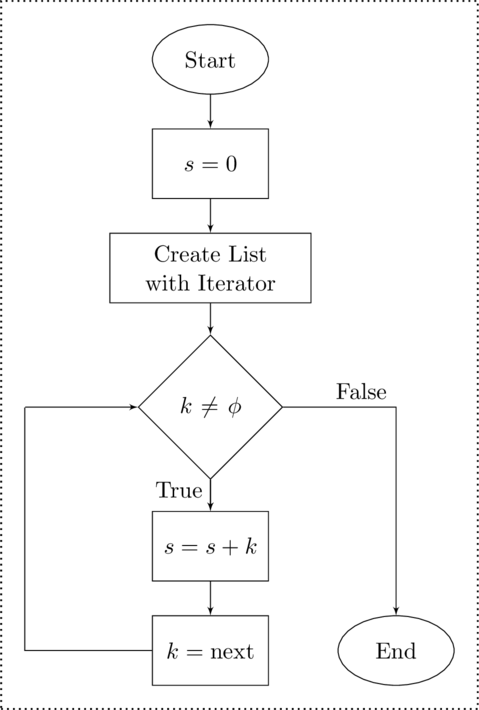
To calculate the Gaussian sum we need to create an accumulator for the sum and set it to zero. The function will then have to create a list of the elements from

to
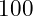
. The
for loop will take care of iterating through the list. Thus the only requirement for each pass through the loop is to update the accumulator with the next value in the list.
function s = gauss_sum(a, b) % Check that b > a if(a > b) error('First value must be smaller than last value'); end % Initialize accumulator s = 0.0; for k = [a:b] % Add to accumulator s = s + k; % for loop automatically steps k to % the next element endend
>> s = gauss_sum(1, 100)s = 5050
Code Sample of a Calculating a Finite Sum Using a For Loop
While this function will run quickly for almost any minimum and maximum input values – it is a
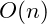
or linear time algorithm – it can be reduced to
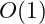
– a constant time algorithm – as Gauss did when he was nine years old.
Gauss observed that if instead of adding each element of the list individually to a running total – his accumulator – you could simply add the first and last values, in this case
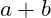
. The same sum occurs if you move one up with
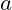
and one down with
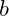
,
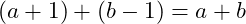
. This continues for every pair of values of which there are
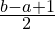
pairs. Using his observation Gauss determined that
(6) 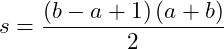
This new equation can be written as a function without any repetition.
function s = gauss_sum(a, b) % Check that b > a if(a > b) error('First value must be smaller than last value'); end % No accumulator % No Loop - just a single equation s = (a + b).*(b - a + 1)./2;end
>> s = gauss_sum(1, 100)s = 5050
Flow Chart and Code Sample of Calculating a Finite Sum Without a Loop
Although a repetition structure is not normally a problem in a program – they do create the ability to perform the same calculation hundreds or even millions of time – they can create time issues.
A single loop has linear complexity, while two loops nested one within the other would be
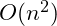
. As the number of passes increases these loops can start to slow down the program. While it is not common that a loop can be replaced with a single calculation, if it can – as the Gauss Sum example shows – it can greatly improve the efficiency of the program.
There is a saying in real estate that the majority of the complaints that home owners have about home ownership can be put into two groups; no water where you want it, and too much water where you don’t. We will add a third – the water pressure is just a bit too low, or perhaps just a bit too high. These three complaints can be adapted almost directly to repetition and loops
How are water and repetition structures related? No water where you need it is analogous to a loop that does not run. Too much water where you do not want it is similar to a loop that never stops. And too low – or too high – water pressure relates to the loop running but stops too soon – or runs just a bit too long. These are commonly described as a loop that never runs, an infinite loop, and the off by one error.
Loop that never runs
The first type of possible error in implementing repetition is that the loop never runs. The best designed repetition algorithm is useless if the program never makes a pass through the loop. Instead of making passes through the loop, the logical test fails and the block of code in the loop never runs. Since the program still runs – and runs to completion – it would most likely result in an incorrect result. As such this would be a logic error.
A problem with the loop is to determine whether or not it actually runs. With modern processors program can run so fast that the user will not notice the difference between the program making a few hundred passes through a loop and not running the loop at all. So how do we know that the program is not making passes through the loop?
Trace:
A trace is a temporary programming line used for debugging – often a print statement – that indicates what is happening at a specific part of the program.
Identifying the error
An easy way to determine if the loop is running is to add a trace to the block of code in the loop as is shown in figure. Recall from Chapter~?? that a trace is just a line of code, usually a print statement, that provides information to the programmer about the code at that point. It is meant as a temporary addition to the program that will be removed – or switched off – when the program is complete.
function check_loop(x, a)% CHECK_LOOP check_loop(x, a) is designed% to run as long as x < a % Set global debug global debug = 1; % Enter loop while (x < a) % Use the debug method for the trace if(debug) fprintf('Made it here\n'); end % Update x x = x + 1.0; endend
>> check_loop(5, 8) Made it here Made it here Made it here
Code Sample of Using a Trace to Determine if a Loop is Running
Adding a trace that prints Made it here to a loop to determine if the loop is running is a simple way to determine if passes are being made. If the loop is running then Made it here will print each time that a pass is made through the loop. If it does not print at all then the loop is not running.
Causes of the error
There are two actions that occur before a pass through a loop that will directly impact whether or not the loop runs; initialization of variables and, for a convergence loop, the logical test, while for the iterative loop the instantiation of the list of elements.
The initialization of variables is a possible cause of the loop never running. If you design a loop to run as long as

, you would need to initialize the variable
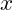
to some value less than
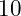
. But imagine that while you wanted
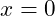
to start, you erroneously set
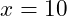
– a common error is switching the initialization value and the test condition. Or using the correct initial value but setting the test condition to
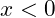
. In either case the initial logical test would fail and the loop would never run.
Infinite loop
The second error is that the loop never stops. This is so common that it has has its own name, the infinite loop. When it starts the loop will continue to run until the user intervenes. In MatLab this is done by using Ctrl C to stop the program.
function check_loop(x, a)% CHECK_LOOP check_loop(x, a) is designed% to run as long as x < a % Set global debug global debug = 1; % Create a counter counter = 0; % Enter the loop while (x < a) % Update counter counter = counter + 1; % Use the debug method for the trace if(debug) fprintf('Pass Number %d\n', counter); end % Update x x = x + 1.0; end % Print a completed step if(debug) fprintf('Completed %d Passes\n', counter); endend
>> check_loop(5, 8) Pass Number 1 Pass Number 2 Pass Number 3 Completed 3 Passes
Code Sample of Using a Trace to Identify an Infinite Loop
Since the program runs but never returns an result, an infinite loop would be considered a runtime error.
Ending an infinite loop:
The user can stop a program that is in an infinite loop by pressing Ctrl C.
Identifying the error
Identifying an infinite loop can be as simple as recognizing that the program is running for an unusual amount of time. This can be problematic because a loop that has to make many passes may be mistaken for an infinite loop.
We can use the trace from before to identify the infinite loop. If we do the Made it here will continue printing on the screen. An improvement to this is to make the two changes in figure Code Sample of Using a Trace to Identify an Infinite Loop. The first is to add a counter to the trace so that you know the number of passes made through the loop. The second is to add an additional trace statement after the loop. This second print statement shows the total number of passes through the loop
Causes of the error
A common issue that can cause an infinite loop is the update – or more specifically the lack of an update. If the update step is missing from the loop block then the logical test will never have a chance to become false. Thus the loop will never end.
A second still involves the update step. In this case the update takes the test value in the wrong direction. For example, if the test is that

with an initialization of
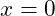
, and an update
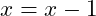
then then value will move farther away from ending instead of closer. In this case the correction is that the update should be
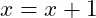
.
Off by one error
There is a third possible error in working with loops – one that could be the most problematic of the three. It is commonly known as the off by one error but in general it means that the loop runs and stops, but it did not run the correct number of times. While the name implies that when the loop runs there is one too few or one too many passes made, in actuality it could be any incorrect number of passes. Similar to the loop that never runs, the off by one error would be considered a logic error.
Identifying the error
Identifying the off by one error is done in the same way as identifying the infinite loop. By using the same debugging traces in figure Code Sample of Using a Trace to Identify an Infinite Loop you will get a count of the number of passes that were made through the loop. If the loop should have made ten passes, but only made nine then the counter will show nine.
Cause of the error
The off by one error is commonly a result of an incorrect logical test. If the loop makes one too few passes it can often be corrected by changing an absolute inequality to an inequality. This means that if the logical test is

then it might need to be
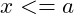
. On the opposite side if the loop makes one too many passes then a logical test
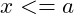
should probably be

.
A second, although less common, problem is the update step. This might be the cause of the off by one error if the loop is making half – or a third, or a quarter – the number of passes than it should. Since a common update is
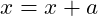
the problem might the value
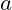
. Instead the update might need to be
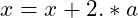
or some other multiple.
Errors with an Iterative Loop
Two of the three repetition errors are possible with the iterative loop (the for loop). These are that the loop never runs, and the off by one error. Since it is impossible to create an infinite list you cannot have an infinite loop with a for loop.
In both of these the error can be found by using the same traces that were used with the convergence loop. If the number of passes is zero, then clearly the loop never ran. If the number of passes is different than the number of elements that you thought were in the list then the loop is showing an off by one error.
The remedy is to review the three limits for the list – the starting value, the stopping value, and the step size. If the starting value is larger than the stopping value and the step is not negative, or it is missing, then the list will be empty and the loop will not run. The same would happen if the starting value is less than the stopping value but the step size is negative. There are no other ways to make an empty list and thus a for loop that never runs.
The off by one error also involves the three limits. The most common is that the step size is incorrect. Recalculate the number of elements – a formula for this will be presented in Chapter Vectors. If the number of elements is not the same as the number of passes that are needed in the loop, then reevaluate the step size.
Number of Elements:
The number of elements in a list can be calculated using
n = floor((stop – start) ./ step) + 1;
It is also possible that the stopping value is incorrect. Remember that the list will end at or below the stopping value. It is not uncommon to erroneously include the stopping value as an element when it is in fact not included.
Repetition is the process in programming that separates the computer from the user. A person can perform even the most complex calculation with a pencil and paper. But what the person cannot do is repeat this calculation millions of times. A computer can perform such repeated calculations by using repetition.
There are two types of repetition, a convergence loop and an iterative loop. Convergence is done using a while loop. In the while loop a logical test is performed to determine if the loop should run. If the result of the test it true then a pass is made through the block of code that forms the loop. Once the pass is completed the test is repeated. This process continues until the logical test returns false. The loop is described as a convergence loop because the process – test, run, update – is repeated until some value converges to the desired result.
Iteration is done with a for loop. Unlike convergence, in a for loop the program creates a list, or vector, of values. With this is a variable known as an iterator. The iterator is assigned the value of the first element of the list and then a pass is made through the loop. At the completion of the pass the iterator is assigned the second element and another pass is made. This process is repeated until each element in the list has been accessed.
While repetition enables to computers to process massive amounts of data they do come with an issue of time. A single loop will normally operate in linear time, while two loops nested one inside of the other will be quadratic. For large amounts of data the polynomial time needed to process the data using multiple nested loops can make an impact on the efficiency of a program. If a loop can be replaced by a single calculation then it is possible to reduce the complexity to a constant time algorithm.
In addition to the complexity issues, loops can fail in three other ways. In each it is a matter of an error in the programming. These are that the loop fails to run, the infinite loop, and the off by one error. In each case adding a trace to the loop can assist in identifying the error if exists and directing you to the appropriate fix.


![]()