Smart data structures and dumb code works a lot better than the other way around.
Eric S. Raymond – Open Source Software Developer
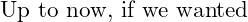
to use a value in a program we had to create a variable. It is a straightforward one to one relationship, one number – one variable, But what if we do not know when we write the program how many values are going to be needed? We could use an accumulator and a single variable multiple times, but then we lose knowledge of the individual values. And what if we need them?
You want to calculate the mean of a set of observations. Easy enough, if you have three observations then
mean = (x1 + x2 + x3) ./ 3;
Since you have three values you create three variables, x1, x2, and x3. But if you need four you will have to change the code.
An alternative is to use a while loop
sum = 0.0;
count = 0;
while(count < n)
sum = sum + x;
count = count + 1;
end
mean = sum ./ n;
The while loop approach eliminates the need to know the number of observations, but you lose the individual values. This becomes an issue if you want to calculate the standard deviation.
What is needed is a method of data management that
- can store multiple values
- does not limit the number of values (can be one or one million)
- allows access to the individual values
- can be handled in the program like a single variable
The solution is to use a type of data structure called an array or a vector.
The most common and widely used data structure is the one-dimensional array called a vector. It is similar to a variable but with an important difference – it can hold multiple pieces of data.
A vector consists of a set of elements. An element is the individual the data item that it being stored in the vector. Each element has an index starting at  .
.
Warning
A vector can be used to store numerical values or characters, but not both.
If a program has a vector called
vec, then
vec(k) is the
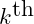
element in the vector.
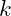
is the index of that element.
There are two types of vectors; row vectors and column vectors. Thinking of this in terms of matrix dimensions a row vector will have one row and

columns or a

matrix of elements. A column vector will have
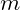
rows and only one column. This would make it an
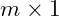
matrix of elements.
Creating a new vector
Vectors are only as useful as their data. But before they are used, they must be created. If a vector were a variable then the variable would be declared. But vectors are not variables in the traditional sense; they are an object. As we create an instance of an object. This process is often instantiating and object, or in this case instantiating a vector.
Instance
In object oriented programming an instance is an occurrence of the object. Creating this instance is called instantiating.
Vectors can be created in three ways; as an empty vector, by enumerating the individual elements, or by creating a range of data.
Creating an empty vector
The more common means of instantiating a vector consist of creating it by filling it with data. But there are many times when you may want a vector that that begins its lifetime with no elements. This is an empty vector.
% An empty vector is created by assigning the [] to itvector = [];
Syntax For Creating an Empty Vector
Once instantiated, an empty vector can be used in the same way as a vector that contains data.
Entering data by enumerating the elements
If the vector has only a few elements it can be created by enumerating; listing the individual elements in the vector separated by commas or spaces.
% Each element is entered in a comma delimited listrowVector = [e_1, e_2, e_3, ... , e_n];
Syntax For Enumeration of a Row Vector
To create a column vector the commas are replaced with semicolons.
% Each element is entered in a semicolon delimited listcolumnVector = [e_1; e_2; e_3; ... ; e_m];
Syntax For Enumeration of a Column Vector
Note:
Row vectors and column vectors behave similarly. The distinction is minor now but will become important when they are used with matrices. Unless you specifically need one or the other it will not normally matter which you use, but you should be consistent. If you use row vectors then stay with row vectors. If you use column vectors then stay with column vectors. Avoid mixing the two in a single operation.
Example Row and Column Vectors with Eight Elements demonstrates creating a row vector called dataRow with eight numerical elements, and another called dataColumn with five, on the command line.
>> % Row vector - each element is comma delimited list>> dataRow = [7, 5, 2, 9, 6, 8, 0, 4]dataRow = 7 5 2 9 6 8 0 4>> % Column vector - each element is semicolin delimited list>> dataColumn = [3; 8; 1; 0; 5]dataColumn = 3 8 1 0 5>>
Row and Column Vectors with Eight Elements
Enumeration is the preferred choice if you just need to enter a small set of values that are not in particular order. But what if you need to create a vector with hundreds or thousands of values?
Entering the elements in a vector as a range
If the data is an increasing or decreasing series with a constant distance between points then you can create the vector as a range of values.
% Elements are determined by a range of valuesrangeVector = [start:step:stop];
Syntax For Indicating the Range of Elements in a Row Vector
In the range approach, you enter three colon delimited values; the starting point, the step size – the distance between each point, and the stopping value. While the first element of the vector will the starting value, the stopping value is a do not exceed value. This means that the final element will be at or below the stopping value but never above it.
The step value is optional. If it is omitted then it defaults to one. A common use of this – as it was in the for loop – is to create a vector with a set of values 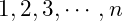 where
where  is set in the program.
is set in the program.
>> % Row vector - unit step from one to eight>> dataRow = [1:8]dataRow = 1 2 3 4 5 6 7 8>> dataRow = [3.2:6.7]dataRow = 3.2 4.2 5.2 6.2>>
Vector with Range from  to
to 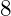
Of course the range can start or stop at any values, positive or negative. If the

then the elements will be increasing. But if
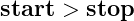
, and
step is omitted an empty vector will be created.
>> % Row vector - increasing range>> incVector = [-4:5]incVector = -4 -3 -2 -1 0 1 2 3 4 5>> % Row vector - decreasing range>> decVector = [6:-2]decVector = [](1x0)>>
Increasing and Decreasing Range of Elements in a Vector
Warning:
If start > stop and step is omitted an empty vector will be created. No warning or error will be given.
The empty vector, as in example
Increasing and Decreasing Range of Elements in a
Vector is created and is accessible. It is a vector like any other it just does not contain any elements. The notation
( )
) indicates that it is a row vector; one row with zero columns.
If
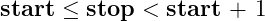
then the vector will contain only a single element. This also covers the case where
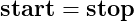
(example
: Creation of a Scalar When stop ≤ stop + 1 ).
>> % stop = start>> scalar = [2:2]scalar = 2>> % stop < start + 1>> scalar = [5:5.7]scalar = 5>>
Creation of a Scalar When 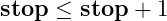
When the step is set the vector is created where each element is step away from the previous element. The final element will not always be stop. As mentioned previously, stop is a do not exceed value. This means that if adding an additional step to value results in an element that is beyond stop then the vector stops with lower value.
>> % Row vector - increasing range>> stepVector = [2:0.7:6]stepVector = 2.7 3.4 4.1 4.8 5.5>> % Row vector - decreasing range>> decVector = [6:-1.3:-2]decVector = 6 4.7 3.4 2.1 0.8 -.5 -1.8>>
Elements in a Vector Where the Stopping Value is not an Element
The elements are created using the recursive formula
(1) ![Rendered by QuickLaTeX.com \begin{eqnarray*} a_k &=& a_{k-1} + \mbox{\textbf{step}}\nonumber\\ a_1 &=& \mbox{\textbf{start}}\nonumber\\ k &=& 2, 3, \ldots, [[1 + (\mbox{\textbf{stop}} - \mbox{\textbf{start}}) / \mbox{\textbf{step}}]] \end{eqnarray*}](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-e2380e0ff36f06338b899d9f7b3434d8_l3.png)
Greatest Integer Function:
The function
![Rendered by QuickLaTeX.com [[x]]](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-0e7ef60afc0bf549ca19acf3f5e848fd_l3.png)
is the greatest integer function (GIF). It is the largest integer that is less than or equal to
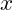
. In MatLab the GIF can be called using
floor(x).
The recursive formula shows that elements will be created in both increasing series, 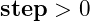 , and decreasing series,
, and decreasing series, 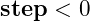 . But if step is in contradiction with the direction of start and stop then the recursive series fails. In this case you will still create a vector, but it will be empty.
. But if step is in contradiction with the direction of start and stop then the recursive series fails. In this case you will still create a vector, but it will be empty.
Warning:
While vectors can be created that are both increasing and decreasing, the sign of step must correspond to the whether the vector elements are increasing or decreasing. If they do not, the vector will be created but it will be empty.
The range method can only be used to create row vectors. If you need to create a column vector then you do so in two steps. First you create the row vector then you take the matrix transpose using the transpose operator (.’). This will transform the row vector into a column vector.
>> % Create the range then take transpose>> colVector = [0:4].'colVector = 0 1 2 3 4>>
Creating a Column Vector Using the Range of Elements
Assigning elements individually
Creating a vector by either enumerating all of the elements or by setting up a range of values is a common method if the values of the elements are know prior to running the program. But there are often times when you need to enter the value of an element one element at a time during the runtime. You can do this by assigning a value to an individual element.
% Syntax For Entering Individual Elementsvector(k) = [e];
Syntax for Creating a Vector by Assigning Individual Elements
An example of this is shown in figure Entering Individual Elements where a new vector is created by first assigning a value to the first element; then the second, and the third, and so on.
>> % Enter values into the individual elements by their index>> vector(1) = 3;>> vector(2) = 5;>> vector(3) = 2;>> vector(4) = 7vector = 3 5 2 7>>
Entering Individual Elements
This is a common approach for when the user will be entering the data through an input prompt as demonstrated in example : Filling a Vector Using a while Loop and a Sentinel Value.
function driver( )% DRIVER driver( ) is the main or driver function % Create an empty vector X = [ ]; % Create a counter and an input variable count = 0; x = 0; % Enter data using a while loop % Use a sentinel value (< 0) to stop fprintf('Enter each value\n'); fprint('(negative to quit)\n'); while(k > 0) k = input('Next value: '); if(x > 0) count = count + 1; X(count) = x; end end % Print the vector using a for loop fprintf('\n X = '); for k = [1:count] fprintf('%d: x = %0.2f ', k, X(k)); end % Print a new line fprintf('\n ', k, X(k));end
>> driver( )Enter each value(negative to quit)Next value: 7Next value: 3Next value: 6Next value: -5X = 7.00 3.00 6.00>>
Filling a Vector Using a while Loop and a Sentinel Value
The example also shows a means of printing the elements of a vector. Since each element can be accessed by its index, a for loop that iterates through a list of the vector indices will also access each element.
There is no requirement that the elements be entered in order. If the index of an element that is being entered is beyond the final element of the current vector, or not  for a new vector, the vector that you create will be filled with zeros up to the index specified. This will also create a new vector if one does not already exist.
for a new vector, the vector that you create will be filled with zeros up to the index specified. This will also create a new vector if one does not already exist.
>> % Enter individual element>> vector(4) = 3;vector = 0 0 0 3>> vector(7) = 8;vector = 0 0 0 3 0 0 8>>
Buffering Vector Elements with Zeros
This technique can be useful when creating a vector of all zeros – although we will later see another way. Assign a value of

to what is to be the last element of a vector. It will be set to

as will all of the elements that come before it.
>> % Enter individual element>> zeroVec(7) = 0;zeroVec = 0 0 0 0 0 0 0>>
Creating a Zero Vector
Reassignment of Elements in a Vector
Vectors are mutable – a term that simply means that the individual elements can be reassigned. Changing individual elements is a matter of reassigning a value to a particular element. This can be done individually – one element at time – or by range.
Assigning a scalar to a single element
The syntax for changing a single element is shown in figure Syntax for Changing an Individual Element of a Vector .
% Assigning a scalar to an element by indicating the index, kvector(k) = [x];
Syntax for Changing an Individual Element of a Vector
When assigning data to a single element of a vector the index of the element is within a set of parentheses, ( ), while the new element can – but is required to – be within a set of square brackets [ ]. This creates a clear demarcation between the data in the element and location or index of that element. The sample code in figure Changing an individual element of a vector demonstrates this.
>> X = [6 3 8 1 4];>> X(2) = [5]X = 6 5 8 1 4>>
Changing an individual element of a vector
Warning:
When reassigning an individual element or a range of elements, the index values are indicated with the vector inside of the parentheses. The values of the elements that will be stored in the vector are collected inside of square brackets.
Assigning a vector to a range of elements
It is also possible to reassign a range of elements using a single command. It is very similar to an assignment to a single element, but the index is replaced with a range of indices, and the scalar value for the element is replaced with a vector. The syntax for this is shown in example Syntax for Changing a Range of Elements of a Vector .
% Assigning a vector to a range indicated by start:step:stopvector(start:step:stop) = [e_1 e_2 ... e_n];
Syntax for Changing a Range of Elements of a Vector
There are several items that need clarification in how updating a range of elements is done.
- Because the range corresponds to the index values in the vector, the values of the range must be integers.
- The minimum value for the range is
 .
.
- If the step is excluded then it defaults to
 .
.
- The range can be increasing or decreasing, but if it is decreasing then the step must be included.
- If the length of the range of elements to be assigned in the range on the left of the assignment operator is
 , then the length of the vector with the data to be assigned must be either
, then the length of the vector with the data to be assigned must be either  or one.
or one.
In this sample code, a range of three is indicated by the
(2:4) and the vector on the right hand side has three elements. Thus the element values
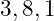
are reassigned to
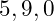
.
>> X = [6 3 8 1 4];>> X(2:4) = [5 9 0]X = 6 5 9 0 4>>
Assigning a vector of elements to a subrange of elements of another vector
Scalar Expansion:
If a vector is being assigned a scalar to a range of elements, the scalar is automatically repeated using scalar expansion until it is the same length as the vector.
What if the right hand side vector has a length of one – that is it only contains a single element? Then the single element is expanded to the same length of the vector using what is known as scalar expansion. This means that the scalar is repeated the number of times that are needed to make it appear as a vector with all elements the same.
>> X = [6 5 9 2 4 1 8 7 3];>> X(3:5) = [3]X = 6 5 3 3 3 1 8 7 3>>
Assigning a scalar to a range of elements in a vector using scalar expansion
The
step parameter makes it possible to assign data to noncontiguous elements of the vector. For example, if you need to change every third element to

then you set
step to
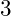
as in figure
Using step to reassign data to noncontiguous elements .
>> X = [6 5 9 2 4 1 8 7 3];>> X(1:3:9) = [0]X = 0 5 9 0 4 1 0 7 3>>
Using step to reassign data to noncontiguous elements
This will also work
right to left – a decreasing range – as long as
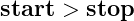
and
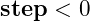
. As always
start,
step, and
stop must be integers.
>> X = [6 5 9 2 4 1 8 7 3];>> X(9:-4:1) = [0]X = 0 5 9 2 0 1 8 7 0>>
Using a negative step to reassign from right to left
In addition to mutability – the ability to reassign values to the elements of a vector – the length of the vector in terms of the number of elements will increase and decrease as elements are added or removed. This means that vectors are dynamic.
Dynamic Vectors
We have seen that we can create vectors and add elements to that vector by assigning a value to an individual element. If the vector does not exist then it is created with the first element assignment. If it does, and the index is beyond the last element of the vector, then the vector is expanded to include the new element. As we have seen the expansion may include the creation of additional elements of which each is assigned the value

. This demonstrates that vectors are dynamic – they can grow with the addition of data. We also see that they can shrink as elements are removed from the vector.
Dynamic Vectors:
A vector that can have data added to it and thus increase the number of elements, or data deleted decreasing the number of elements is a dynamic vector.
Vectors, being dynamic, can increase in length by adding elements or decreased by deleting elements.
Appending elements onto a vector
We have already seen an example of expanding a vector; assigning a value to an element beyond the current end of the vector. Examples of this are in figures Syntax for Creating a Vector by Assigning Individual Elements and Buffering Vector Elements with Zeros. In both cases this is known as appending – adding data to then end of a list or a vector.
Appending
Appending data consists of adding elements to the end of a vector, thus increasing the length of the vector.
% Appending elements after the end of a vector of length n% Note m > n and is an integervector(m) = [e_1 e_2 ... e_k];
Syntax for Appending Elements onto a Vector
Appending data is not limited to single elements. Vectors can be appended onto the tail of a vector as long as the range of the index values matches the number of elements in the vector to be appended. As with scalars, if you append a vector at a point beyond the current final element then the additional elements will be created with the value

. The
step parameter can also be set so that the vector being appended is not contiguous but instead separated by elements with the value

.
>> X = [3 7];>> % Append a vector onto the tail>> X(3:4) = [5 1]X = 3 7 5 1>> % Append a vector beyond the tail with a step value>> X(7:2:9) = [6 8]X = 3 7 5 1 0 0 6 0 8>> % Append a scalar with a repeat of the value>> X(10:2:12) = [2]X = 3 7 5 1 0 0 6 0 8 2 0 2>>
Appending a vector onto the end of another vector
Inserting elements within a vector
It is also possible to add elements to the head of a vector – the beginning – or the middle. Unlike appending this is known as insertion.
There is a slight difference in the syntax when inserting a vector at the head or tail than there is when inserting it within the middle of a different vector.
% Inserting elements at the head of a vectorvector = [ [e_1 e_2 ... e_k] vector];% Inserting elements at the tail of a vectorvector = [ vector [e_1 e_2 ... e_k] ];
Syntax for Inserting Elements at the Head or Tail of a Vector
Insertion consists of creating a new vector consisting of the current vector and the scalar or vector to be inserted. Once created this new vector is assigned to the current vector, replacing it.
The difference that occurs when inserting within the vector is that the original vector must be split at the insertion point. The portion that is to remain in the front of the insertion point is indicated by its range while the remaining subvector is placed after the inserted vector and is indicated by its original range.
Warning:
When inserting a vector into the middle, the ranges that are indicated are those of the current vector before the insertion.
% Inserting elements after the mth element of a vector of length n% Note 1 <= m <= n and is an integervector = [vector(1:m) [e_1 e_2 ... e_k] vector(m+1:n)];
Syntax for Inserting Elements into a Vector
In figure
Inserting a vector onto the head and in the middle of another vector the second insertion takes place at index
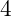
. Thus the first three elements of the current vector are placed in the new, temporary, vector. After the vector that is to be inserted, the remaining elements of the original vector are placed at the tail. Since the remaining vectors started at the old index of
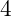
the are indicated with the old index value despite now being at index
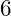
.
>> X = [3 7];>> % Insert a vector at the head>> X = [[5 1] X]X = 5 1 3 7>> % Insert a vector in the middle>> X = [X(1:3) [6 8] X(4)]X = 5 1 3 6 8 7>>>> % Insert a vector at the tail>> X = [X [4 2]]X = 5 1 3 6 8 7 4 2>>
Inserting a vector onto the head and in the middle of another vector
Inserting elements can be implemented individually – as a single element – or as an additional vector. With the insertion approach a new – albeit unnamed vector is temporarily created. Once the insertion is completed the temporary vector is assigned to the original vector – replacing the old with the new.
Note:
Appending elements onto the tail of a vector allows the ability to buffer missing elements with zeros and also the ability to set a step value to have the appended vector skip elements by adding in zero values. Inserting does not. Any vector or scalar inserted will done by creating a gap in the original vector and filling that gap with the new elements.
The number of elements in a vector can be increased by insertion anywhere in the vector – head, middle, or tail – and also by appending onto the tail.
But in keeping with the dynamic nature of vectors – if elements can be added they should be able to be removed. Thus elements can be deleted as well.
Deleting elements from a vector
Deleting an element or a set of elements from a vector is accomplished in the same way if the elements are at the head, the middle, or the tail. In fact it is not so much a matter of deleting the elements as it is reassigning them with … nothing.
To delete an element, a range of elements, or selected elements you reassign them with the empty vector, [ ].
% Deleting elements from an interval of a vectorvector(start:step:stop) = [];
Syntax for Deleting Elements from a Vector
In its most basic – deleting a single element – you set that element to the empty vector. After doing so will realign the indices for the vector so that all of those after the deleted element will shift one to the left.
>> X = [1:15];>> % Delete the fifth element>> X(5) = []X = 1 2 3 4 6 7 8 9 10 11 12 13 14 15>> % Delete the current 7th through 9th element>> X(7:9) = []X = 1 2 3 4 6 7 11 12 13 14 15>>>> % Delete every third element of those remaining>> X(3:3:length(X)) = []X = 1 2 4 6 11 13 14>>
Deleting an Element or a Range of Elements from a vector
Appending and inserting elements is reversible. As long as you retain the length of the original vector or the location of the inserted elements you can then delete them. But not so with deletion. Once elements are deleted they are gone.
Vectors provide a means of storing and moving data through a program with only a single variable. This includes passing vectors to a function and returning them from functions. Whether the operations with vector take place within a function or outside of one, the computations can take advantage of their multiple data elements.
These calculations happen in two ways; as one-dimensional matrices or as individual elements. The first will follow the properties of matrix operations while the latter is done element-wise.
Element-Wise Operations
The most common use of vectors is in element-wise operations. In this type of operation computations are performed between a vector and a scalar, or two vectors of the same type and size.
Element-wise operations with vectors are operations in which the computation is performed between the elements in the first vector with the elements in the same location of the second. Thus if you have two vectors, X and Y then the first element of X will be matched with the first element of Y. The second of each will be paired, and the third, and so forth.
If we use

to indicate any element-wise operation then
(2) ![Rendered by QuickLaTeX.com \begin{eqnarray*} Z &=& \left[a_1, a_2, \ldots, a_n\right]\odot\left[b_1, b_2, \ldots, b_n\right]\nonumber\\ &=& \left[ a_1\odot b_1, a_2\odot b_2,\ldots, a_n\odot b_n\right] \end{eqnarray*}](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-2b83792cf9209ec45e8c50c8404e402a_l3.png)
Warning:
The sample code in figure Adding the elements of two vectors using a for loop is included to show how an element-wise operation could be written. It is included simply as a chance to look under the hood. You should not actually write your vector operations using for loops but instead use the element-wise operators.
While element-wise operations are built in as callable operators, it is possible to write code using a single for loop that perform an element-wise operation on two vectors – or a vector and a scalar. A demonstration of this in figure Adding the elements of two vectors using a for loop.
function driver( )% DRIVER driver( ) is the main or driver function % Set the length n = 8; % Create two vectors X = [3, 4, -3, 6, 8, -7, -1, 9]; Y = [6, 1, 5, 9, 7, 2, -3, 4]; % Start a for loop to add the elements of the % two vectors. The iterator a list from 1 to n for k = 1:n % Add the corresponding elements Z(k) = X(k) + Y(k); end % Show the elements of Z Zend
>> driver( ) - Z =
- 9 5 2 15 15 -5 -4 13
- >>
Adding the elements of two vectors using a for loop
Although any of the element-wise operations can be written using a for, loops, especially iterative loops, are considered slow when using an interpreted language. As such they should be avoided. Instead MatLab provides built-in operators for the five element-wise operations between vectors, addition +, subtraction -, multiplication .*, division ./, and exponentiation .\pow.
% AdditionvectorSum = vec_1 + vec_2;% SubtractionvectorDifference = vec_1 - vec_2;% ProductvectorProduct = vec_1 .* vec_2;% QuotientvectorQuotient = vec_1 ./ vec_2;% PowervectorPower = vec_1 .^ vec_2;
Syntax for the Five Element-Wise Operations
Element-wise calculations are the standard when performing any calculation with vectors as examples Demonstrating Element-Wise Operations with Two Vectors and Demonstrating Element-Wise Operations with Vector and Scalar show.
Note:
A question about calculations is often asked. “Why use .*, ./, and .\pow instead of the the commonly accepted .*, ./, and .\pow? The more common operators are used for matrix operations. The dot operator is used to differentiated matrix from element-wise operations.
A question is often asked about calculations. “Why use .*, ./, and .\pow instead of the same operator without the dot? After all, it works just fine with scalars.”
The answer is that all operations were originally meant to be used with matrices in matrix operations. Because of this the common operators for multiplication, division, and exponentiation were assigned to their matrix calculation. And yes, it does work for scalars because a scalar is a  matrix and for scalars the matrix operations and the element-wise operations are the same. But they are not the same for vectors or other matrices.
matrix and for scalars the matrix operations and the element-wise operations are the same. But they are not the same for vectors or other matrices.
This is also the reason that you do not need the dot for + or –. Matrix addition and subtraction are the same as element-wise addition and subtraction. Since there is no difference there is no need for the dot.
function driver( )% DRIVER driver( ) is the main or driver function % Create vectors X = [6, 3, 9, 7] Y = [2, 0, 3, 1] % Addition A = X + Y % Subtraction S = X - Y % Multiplication M = X .* Y % Division D = X ./ Y % Exponentiation E = X .^ Yend
>> driver( )X = 6 3 9 7Y = 2 0 3 1A = 8 3 12 8S = 4 3 6 6M = 12 0 27 7D = 3 inf 3 7E = 36 1 729 7>>
Demonstrating Element-Wise Operations with Two Vectors
If the operations are between a vector and a scalar then the scalar expansion is performed so that the scalar is the same length as the vector. From there the usual element-wise operations are done. Of course the scalar expansion is never seen.
function driver( )% DRIVER driver( ) is the main or driver function % Create a scalar and a vector a = 4; X = [2, 0, 3, 1]; % Addition A = a + X % Subtraction S = a - X % Multiplication M = a .* X % Division - Scalar Denominator DSD = a ./ X % Division - Vector Denominator DVD = a ./ X % Exponentiation - Scalar Base ESB = a .^ X % Exponentiation - Vector Base EVB = X .^ aend
>> driver( )A = 6 4 7 5S = 2 -4 1 3M = 8 0 12 4DSD = 0.5 0 0.75 0.25DVD = 2 inf 1.33 4ESB = 16 1 64 4EVB = 16 0 81 1>>
Demonstrating Element-Wise Operations with Vector and Scalar
Matrix Operations with Vectors
While we commonly think of vectors as a data structure to store and manipulate multiple elements, they are at the most basic a one-dimensional matrix. A row vector is a

matrix and a column vector is an
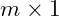
matrix.
Note:
Using the operator with the dot or without when adding, subtracting, or multiplying a vector and scalar will not change the result. A matter of consistency is to choose the operator based upon whether the operations are meant to be matrix or element-wise. If matrix operations then do not use the dot. If element-wise then use the dot.
Matrix operations with a vector and a scalar are the same regardless of whether it is done using element-wise or matrix calculation. As such, if you are adding, subtracting, multiplying a vector and a scalar the choice of operator, with the dot or without, does not matter.
If the row vector is multiplied to the column vector then each must have the same dimension (number of elements). But the dimensions of the two vectors do not have to be the same if it is the column vector multiplying the row vector. Recall that when multiplying matrices the columns of the first must match the rows of the second. Thus for two vectors
(3) 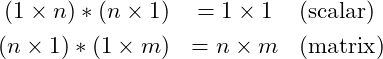
The first product, the scalar, is the dot product or scalar product. It is a common calculation in engineering for calculating the magnitude of a vector or the angle between two vectors.
Dot Product:
The dot product, or scalar product is the matrix product of a row vector and a column vector of the same length. It is calculated as the sum of the products of each matching element. It can be used to determine the angle between two vectors.
The magnitude of a vector is its length. It is calculated by
(4) 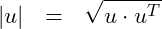
The magnitude can be calculated as a single line code – that can be run on the command line – in which a vector is multiplied using the matrix product with its own transpose (figure Dot product to calculate the magnitude of a vector ).
>> X = [4, -3, 6];>> % Calculate the magnitude as the matrix product with its transpose>> magX = sqrt(X * X.')magX = 7.8102>>
Dot product to calculate the magnitude of a vector
The dot product can be used to calculate the angle between two vectors.
(5) 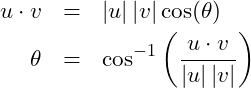
there are two different vectors then the dot product can be used to calculate the
The sample code in figure
Dot product to calculate the angle between two vectors demonstrates using the vector product to calculate the angle between two vectors in
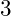
-space.
function driver( )% DRIVER driver( ) is the main or driver function % Create two vectors X = [4, -3, 6]; Y = [1, 5, -2]; % Calculate the magnitude of each of the two vectors % Need to take the transpose of the second vector magX = sqrt(X * X.'); magY = sqrt(Y * Y.'); % Calculate the dot product by multiplying two vectors % Need to take the transpose of the second vector dotProduct = X * Y.'; % Calculate the angle between the vectors angle = acosd(dotProduct ./ (magX .* maxY); % Print the results fprintf('Angle: %0.2f degrees\n', angle);end
>> driver( )Angle: 122.52 degrees>>
Dot product to calculate the angle between two vectors
Vectors calculations can be made both element-wise and matrix wise. This puts the vector on the same level as scalars in terms of calculation, but can vectors be compared to one another? And what would comparing two vectors even mean?
Is it possible for a vector to be smaller, or larger than a scalar? How about two vectors? Can one vector be smaller than the second. In a basic sense – no. The magnitude of each vector can be compared or the magnitude of a vector can be compared to a scalar, but not the entire vector.
Comparing the magnitude of two vectors – or the magnitude of a vector to a scalar is an application of the dot product. As an example, figure Comparing the magnitude of two vectors demonstrates how to determine if the magnitude of one vector is larger than than other.
- f
unction driver( )
% DRIVER driver( ) is the main or driver function % Create two vectors X = [4, -3, 6]; Y = [1, 5, -2]; % Calculate the magnitude of each of the two vectors % Need to take the transpose of the second vector magX = sqrt(X * X.'); magY = sqrt(Y * Y.'); % Compare the vector magnitudes if(magX > magY) fprintf('Vector X is larger than Vector Y\n'); else fprintf('Vector X is not larger than Vector Y\n'); endend
>> driver( )Vector X is larger than Vector Y>>
Comparing the magnitude of two vectors
Since in engineering we often use vectors in their traditional sense of a ray with direction and magnitude, this application would be used to determine which vector is longer. But this application is not a comparison of vectors as much as it is a comparison of scalars – which we have done before.
Comparing vectors as data structures is different from comparing them as geometrical vectors. In the data structure implementation vectors are compared element-wise. This means that if a relational operation between two vectors,
X and
Y will result in a third vector where each element indicates with true or false (

or

)
function driver( )% DRIVER driver( ) is the main or driver function % Create two vectors X = [3, 4, -3, 6, 8, -7, -1, 9]; Y = [6, 1, 5, 9, 7, 2, -3, 4]; % Compare the vectors element-wise % This will result in a vector of 0s an d1s TorF = (X < Y) % Number of ones numOnes = TorF * TorF.' % Number of zeros numZeros = (1-TorF) * (1-TorF).'end
>> driver( )TorF = 1 0 1 1 0 1 0 0numOnes = 4numZeros = 4>>
Comparing the elements of two vectors
In this example, figure Comparing the elements of two vectors, each element is compared with the result being its logical value.
Note
A useful addition to this would be know how many of the elements are zero or one. While we will later see several functions that will do this directly we could adapt the code to provide us the number of

s and the number of

s. Recall that the dot product of a vector with itself will return a sum of the squares of the elements. And since all of the elements are either

or

then the sum of squares will be the number of true values. If we then subtract each element from

and repeat it we will have the number of zeros.
This same approach is used when comparing a vector to a scalar. In this matter the scalar is expanded to the same length of the vector and each element of the vector is then compared to the same value. This can be used, as in the example in figure Comparing the elements of a vector with a scalar to see if all of the elements are above some minimum value. And if they are not, which elements fail the test.
function driver( )% DRIVER driver( ) is the main or driver function % Create two vectors X = [5, -5, 2, 9, -1, 3, 0, 6]; a = 0; % Compare the vector to the scalar % This will result in a vector of 0s an d1s TorF = (X >= a) % Number of ones numOnes = TorF * TorF' % Number of zeros numZeros = (1-TorF) * (1-TorF).'end
>> driver( )TorF = 1 0 1 1 0 1 1 1numOnes = 6numZeros = 2>>
Comparing the elements of a vector with a scalar
Vector operations can be implemented both element-wise and matrix wise. They can also be compared element-wise to another vector or by scalar expansion to a single scalar. We have developed these operations to be performed outside of functions, but in keeping with our goal of top-down design we need to be to hide them away within functions as well.
The relationship between vectors and functions are similar to those with scalars. Vectors can be passed as a parameter to a function, and they can be returned as an output from a function. But is also possible to have scalar inputs with vector outputs, vector inputs with vector outputs, and vector inputs with scalar outputs.
Functions that are passed vectors and return vectors
Most functions in which a vector is passed returns a vector consisting of the elements calculated using element-wise operations. This is the case for any of the computation functions like the trigonometry functions sin, cos and tan. This is the same for the algebraic functions such as log, exp.
An example of a code in which a vector is passed to the cos function and the return vector is then part of an additional element-wise calculation is shown in figure Element-Wise Operations in Evaluating a Built-In Function.
>> % Create vector>> X = [0, 30, 45, 60, 90]>> % Evaluate the cosine with angle in degrees>> Y = cosd(X)Y = 1.00000 0.86603 0.70711 0.50000 0.00000>>
Element-Wise Operations in Evaluating a Built-In Function
Element-wise calculations with a vector return are the common result of most local and anonymous functions.
>> % Create the anonymous function>> f = @(x) x.^2 + 3.*x - 10;>> X = [-3, -2, -1, 0, 1, 2, 3, 4];>> % Evaluate the function>> Y = f(X)Y = -10 -12 -12 -10 -6 0 8 18>>
Element-Wise Calculations in an Anonymous Function
It should not be assumed that functions that are passed and return vectors are simply computational. There are many applications in which you need to rearrange elements in a vector or sort them in ascending – lowest to highest – or descending – highest to lowest – order. These will be addressed in section Sorting Elements in a Vector.
Functions that are passed scalars and return vectors
Most of the functions with which we have dealt have been computational; pass scalar values as input parameters – calculate and returns another scalar. With vectors and element-wise operations nothing changes. We pass a vector or vectors to the function, and it uses them to calculate and return another function.
But there are functions that are passed individual scalars and these are used to create a vector.
Example: A common issue in creating a vector is determining the correct step size for the range. Say you want a vector with just five elements from  to
to 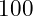 . Many people would erroneously say the step should be set at
. Many people would erroneously say the step should be set at 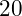 but this would create a vector with six elements. Close, but six is not five.
but this would create a vector with six elements. Close, but six is not five.
step should not have been set to 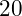 but instead to
but instead to 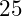 .
.
The step size for a vector given the start and stop values with a set number of elements could be calculated in a function and the function could then create and return the vector with the correct number of elements. The step size – or the number of elements – can be calculated using the formula
(6) 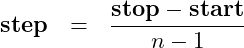
The number of elements is decreased by one,
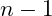
, because the divisor is not the number of elements but instead the number of steps. For any vector there will always be one less step than there are elements.
If needed, equation~
6 can be solved for

to determine the number of elements.
(7) ![Rendered by QuickLaTeX.com \begin{eqnarray*} n &=&\left [\left[ \frac{\mbox{\textbf{stop}} - \mbox{\textbf{start}}}{\mbox{\textbf{step}}} + 1\right]\right] \end{eqnarray*}](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-3a5e0b027cc3d90c535a73a2942cc01a_l3.png)
The formula in equation~
6 can also be used to create a local function that creates a vector.
function V = makeLinearVector(start, stop, n)% MAKELINEARVECTOR V = makeLinearVector(start, stop, n) creates% a row vector with elements spaced linearly starting at start and stopping% at stop with n elements % Calculate the step size step = (stop - start) ./ (n - 1); % Create the vector V = [start:step:stop];end
>> X = makeLinearVector(3, 17, 8)X = 3 5 7 9 11 13 15 17>>
Creating a Linearly Spaced Vector
linspace(start, stop, n):
The sample code in figure
Creating a Linearly Spaced Vector demonstrates how to create a vector from the overall range and the number of elements. This code does not include the necessary error checking –
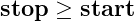
and
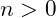
and and also an integer,
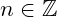
. While we could add this, there is already a built in function to do that for us,
linspace(start, stop, n)
There is a built in function that does the same as the example function V = makeLinearVector(start, stop, n). It is V = linspace(start, stop, n).
In engineering it often occurs that we need a vector of values that spaced logarithmically, not linearly. For example, instead of a vector
![Rendered by QuickLaTeX.com \mbox{\textbf{V}} = [0, 1, 2, \ldots, n]](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-bebd2b8091a6b060db34af96f00b4e6c_l3.png)
, the vector needed is
![Rendered by QuickLaTeX.com \mbox{\textbf{V}} = [10^0, 10^1, \ldots, 10^n]](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-1ea25cd314a4db2af29bd53a6c02a553_l3.png)
. This can be done using the
makeLinearVector function (or
linspace) and the element-wise power operator in figure
Creating a Logarithmically Spaced Vector.
logspace(start, stop, n):
Much like linspace there is a built-in function to create the logarithmically space function. It is logspace(start, stop, n).
function v_log = make_log_vector(start, stop, n)% MAKE_LOG_VECTOR V = make_log_vector(start, stop, n) creates% a row vector starting at 10.^start and stopping at 10.^stop with n elements%. logarithmically spaced % Create a linear vector v_lin = makeLinearVector(start, stop, n); % Element-Wise Power Operator v_log = 10.^v_lin;end
>> X = make_log_vector(0, 3, 8)X = 1.0000 5.6234 31.6228 177.8279 1000.0000>>
Creating a Logarithmically Spaced Vector
Note:
The built-in functions linspace and logspace perform the same actions, so why create local function? In this case it is a matter of generalization. The built-in function is convenient but the local function can be adapted to, for example, a binary growth function by changing V = 10.\pow VLin to V = 2.\pow VLin.
The sample function makeLogVector performs the same operation as calling the built-in function VLog = logspace(start, stop, n);
There are several functions similar to linspace and logspace but they are designed to return matrices. But they are useful enough in creating vectors to adapt them here. Three in particular are zeros, ones, and rand. So while we can use them as matrix functions and then force them to create vectors, we could just write our own local functions that create the vector directly.
The first two are easy. We can set
start =

, and
stop =

and then fill the elements with the value

or

.
function zeroVector = makeZeroVector(n)% MAKEZEROVECTOR zeroVector = makeZeroVector(n) creates a row% vector starting of n elements all with the value 0 % Set start to 1 and use n for stop and use scalar expansion to % fill all of the elements with zero zeroVector[1:n] = 0;end
>> Z = makeZeroVector(7)Z = 0 0 0 0 0 0 0>>
Creating a Zero Vector
While

and

are commonly used when creating an accumulator for sums or products, this technique can be used to create a vector with any starting value. For a different starting value, you change the assignment value in the function.
This type of function can actually be generalized for such as case by passing two input parameters to the function. The first is for the number of elements while the second is the value. If the user wants a default value, such as

then the function can use the
nargin variable to overload it. An example of this is shown in figure
Creating a Vector with a single repeated value.
function valueVector = makeValueVector(n, a)% MAKEVALUEVECTOR valueVector = makeValueVector(n) creates a% row vector with n elements all with the value a % Check nargin. If nargin == 1 then default to 0 if((nargin < 1) | (nargin > 2)) % Exit with run time error for improper number of parameters error('Incorrect number of inputs to makeValueVector'); elseif(nargin == 1) % Set to the default of 0 a = 0; end % Set start to 1 and use n for stop and use scalar expansion to % fill all of the elements with a valueVector[1:n] = a;end
>> V = makeValueVector(7, 3)V = 3 3 3 3 3 3 3>>
Creating a Vector with a single repeated value
Functions that are passed vectors and return scalars
There are a class of functions that when they are passed a vector of data they analyze the vector and return some value based upon that analysis.
Probably the most useful of this type of function is one that calculates the number of elements in the vector. A function that is passed a vector could then count the number of elements using a for loop that iterates through the vector each time updating an accumulator.
function n = length(X)% LENGTH n = length(X) counts the number of% elements in a vector % Set the accumulator to 0 n = 0; % Use a for loop to iterate through the vector for k = X % Update the accumulator n = n + 1; endend
>> n = length([6 2 3 8 1 0 9 3])n = 8>>
Function to return the number or elements in a vector
Warning:
MatLab provides a built-in function, length, that does the same operations as in the local function in figure Function to return the number or elements in a vector. As such there is little reason to add the local function to a program. Instead call n = length(X); directly when you need to know the number of elements.
It makes little sense to add this local function to a program since it has already been written and is built-in. The built-in function is length(X).
While you would probably not write this function, it demonstrates how a function can be passed a vector and then analyze the vector returning a result. There are many such direct applications that could be written but because of the utility have already been included as built-in functions.
An example of this has already been demonstrated with the calculation of the dot product. This can be rewritten as a function; either a local function or an anonymous function.
function dp = dot_product(X, Y)% DOT_PRODUCT dp = dot_product(X, Y) calculates the dot product of two% vectors - it checks that the first vector is a row and the second a column vector % Check nargin. If nargin == 1 then it calculates the magnitude if((nargin < 1) || (nargin > 2)) % Exit with run time error for improper number of parameters error('Incorrect number of inputs to calculate dot product'); elseif(nargin == 1) % Set to the default of 0 dp = 0; else end % Set start to 1 and use n for stop and use scalar expansion to % fill all of the elements with a valueVector[1:n] = a;end
>> X = [4, 7, 3, 1];>> Y = [9, 2, 6, 5];>> D = dot_product(X, Y)D = 73>>
Dot Product Function
It often occurs that the elements in a vector are not where we would like them to be. Perhaps two or more elements should be rearranged, or an entire vector needs to be sorted in either ascending or descending order. There is a built-in function to sort the elements of a vector in ascending order, but perhaps you need the vector in descending order. Or you only need several elements rearranged. In these cases you might want to customize the control of the elements.
Swapping elements in a vector
Sorting elements in a vector begins with being able to
swap them. As an example, we want to swap the element at index
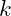
with the element at index
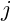
. This function, let’s call it
swap, will require three inputs; a vector, and the two indices for the elements to be swapped.
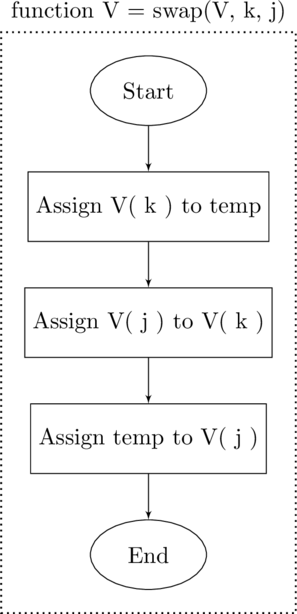
function V = swap(V, k, j)% SWAP V = swap(V, k, m) swaps the% elements in index k of the vector% V with index j of the same vector % Copy the first element to temp temp = V(k); % Reassign the first element with % the value in the second V(k) = V(j); % Reassign the second element with temp % with the value in temp V(j) = temp;end
>> X = [1:5]X = 1 2 3 4 5>> X = swap(X, 2, 5)X = 1 5 3 4 2>>
Function to swap elements
Note:
A common error in a swap is omitting the intermediate temp variable. An analogy is to imagine a farmer with a pen of chickens and another with feed for the chickens to eat. He needs to swap the chickens and the feed. If he put the chickens directly in with the feed they would start to eat the feed. Similarly if he put the feed directly in with the chickens. Instead he needs a temporary third pen. He then transfers the chickens to the temporary pen. He then moves the feed to the now empty pen that previously was full of chickens. Once the feed has been moved he can then transfer the chickens over to their new pen – and then remove the temporary enclosure.
The swap function has multiple applications but probably the most common is in sorting the elements of a vector.
Sorting a vector
sort:
The sort function is passed a vector, either a row vector or a column vector, and it returns the vector sorted in ascending order. The syntax is
V_sorted = sort(V_unsorted);
If the input and output vectors are the same the original will be replaced. But if they are different then there will be two instances of the vector – one sorted and one not.
Vectors that are created using a range are already sorted; lowest to highest or highest to lowest. But if the vector was created by enumerating the elements or appending data, or if data is inserted into a vector it may no longer be sorted. There is a built-in function, sort, that will sort a vector in ascending order, but you may want to sort the data in descending order, or perhaps only sort every other element. As such there are many different types of sorts as well as techniques to sort the vectors.
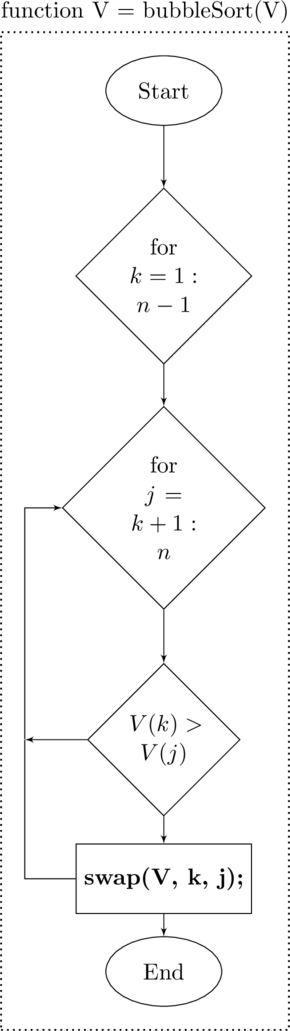
A common, and easy to code – sort algorithm is called the
bubble sort. This technique uses a pair of nested for loops. In this method the outer loop steps through the
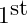
through
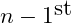
element of the vector. Each iteration starts the inner loop which compares the outer loop element to each element of the vector from the
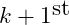
to the
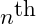
element. At each step if the elements are out of order then they are swapped – can be done with the
swap function.
function V = bubble_sort(V)% BUBBLE_SORT V = bubble_sort(V) uses% a bubble sort algorithm to sort% the vector from lowest to highest % Outer loop for k = 1:length(V) - 1 % Start inner loop for j = k+1:length(V) % Check order if(V(k) > V(j)) % Out of order so swap V = swap(V, k, j); end % End of if end % End of inner loop end % End of outer loopend
>> X = [4, 1, 5, 3, 2]X = 4 1 5 3 2>> X = bubbleSort(X)X = 1 2 3 4 5>>
Bubble sort function
![]() .
.![]() where
where ![]() is set in the program.
is set in the program.![]() to
to ![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*} a_k &=& a_{k-1} + \mbox{\textbf{step}}\nonumber\\ a_1 &=& \mbox{\textbf{start}}\nonumber\\ k &=& 2, 3, \ldots, [[1 + (\mbox{\textbf{stop}} - \mbox{\textbf{start}}) / \mbox{\textbf{step}}]] \end{eqnarray*}](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-e2380e0ff36f06338b899d9f7b3434d8_l3.png)
![]() , and decreasing series,
, and decreasing series, ![]() . But if step is in contradiction with the direction of start and stop then the recursive series fails. In this case you will still create a vector, but it will be empty.
. But if step is in contradiction with the direction of start and stop then the recursive series fails. In this case you will still create a vector, but it will be empty.![]() for a new vector, the vector that you create will be filled with zeros up to the index specified. This will also create a new vector if one does not already exist.
for a new vector, the vector that you create will be filled with zeros up to the index specified. This will also create a new vector if one does not already exist. .
. .
. , then the length of the vector with the data to be assigned must be either
, then the length of the vector with the data to be assigned must be either  or one.
or one.![Rendered by QuickLaTeX.com \begin{eqnarray*} Z &=& \left[a_1, a_2, \ldots, a_n\right]\odot\left[b_1, b_2, \ldots, b_n\right]\nonumber\\ &=& \left[ a_1\odot b_1, a_2\odot b_2,\ldots, a_n\odot b_n\right] \end{eqnarray*}](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-2b83792cf9209ec45e8c50c8404e402a_l3.png)
![]()
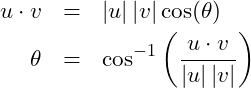

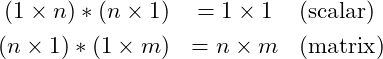
![Rendered by QuickLaTeX.com \begin{eqnarray*} n &=&\left [\left[ \frac{\mbox{\textbf{stop}} - \mbox{\textbf{start}}}{\mbox{\textbf{step}}} + 1\right]\right] \end{eqnarray*}](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-3a5e0b027cc3d90c535a73a2942cc01a_l3.png)