Section 1.8 Quadric Surfaces II
1.8 Quadric Surfaces II
In this section, we practice more quadric surface drawing and identifying.
Common Quadratic Surfaces: Ellipsoid, Hyperboloid of One Sheet, Hyperboloid of Two Sheets, Cone, Elliptic Paraboloid, Hyperbolic Paraboloid.
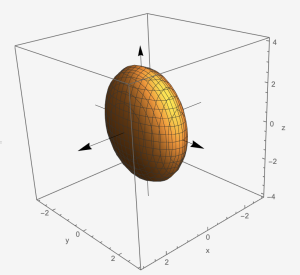
Ellipsoid: [latex]\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1[/latex]
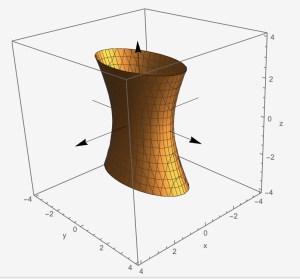
Hyperboloid of One Sheet: [latex]\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=1[/latex]
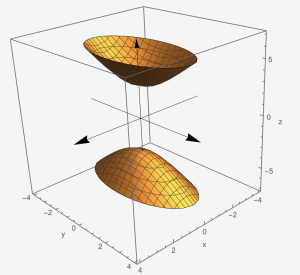
Hyperboloid of Two Sheets: [latex]-\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1[/latex]
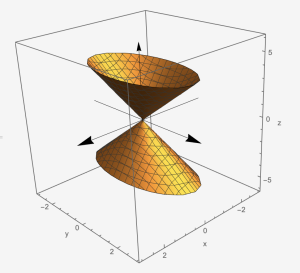
Cone: [latex]\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=0[/latex]
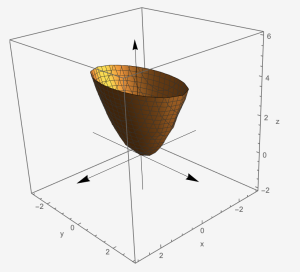
Elliptic Paraboloid: [latex]\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z}{c}=0[/latex]
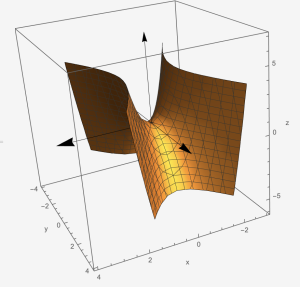
Hyperbolic Paraboloid: [latex]\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}-\frac{z}{c}=0[/latex]
Example 1: Sketch the graph of the surface and identify the surface in the space: [latex]x+3z=6[/latex]
Exercise 1: Sketch the graph of the surface and identify the surface in the space: [latex]4y-z=8[/latex].
Example 2: Sketch the graph of the surface and identify the surface in the space: [latex]x-2y+3z=6[/latex]
Exercise 2: Sketch the graph of the surface and identify the surface in the space: [latex]2x-4y+z=8[/latex].
Example 3: Sketch the graph of the surface and identify the surface in the space: [latex]y=-z^{2}-4[/latex].
Exercise 3: Sketch the graph of the surface and identify the surface in the space: [latex]x=-z^{2}+4[/latex].
Example 4: Sketch the graph of the surface and identify the surface in the space: [latex]x^{2}=-4y^{2}-z^{2}+16[/latex].
Exercise 4: Sketch the graph of the surface and identify the surface in the space: [latex]9x^{2}+y^{2}=-z^{2}+9[/latex].
Example 5: Sketch the graph of the surface and identify the surface in the space: [latex]\frac{x}{2^{2}}=\frac{y^{2}}{3^{2}}+\frac{z^{2}}{5^{2}}[/latex].
Exercise 5: Sketch the graph of the surface and identify the surface in the space: [latex]y=\frac{x^{2}}{3^{2}}+\frac{z^{2}}{1^{2}}[/latex].
Example 6: Sketch the graph of the surface and identify the surface in the space: [latex]\frac{x^{2}}{1^{1}}-\frac{y^{2}}{2^{2}}=\frac{z^{2}}{3^{2}}[/latex].
Exercise 6: Sketch the graph of the surface and identify the surface in the space: [latex]\frac{x^{2}}{3^{2}}=\frac{y^{2}}{1^{2}}-\frac{z^{2}}{2^{2}}[/latex].
Example 7: Sketch the graph of the surface and identify the surface in the space: [latex]-\frac{x^{2}}{1^{2}}-\frac{y^{2}}{2^{2}}+\frac{z^{2}}{3^{2}}=1[/latex].
Exercise 7: Sketch the graph of the surface and identify the surface in the space: [latex]\frac{x^{2}}{3^{2}}-\frac{y^{2}}{1^{2}}-\frac{z^{2}}{2^{2}}=1[/latex].
Example 8: Sketch the graph of the surface and identify the surface in the space: [latex]-\frac{x^{2}}{1^{2}}+\frac{y^{2}}{2^{2}}+\frac{z^{2}}{3^{2}}=1[/latex].
Exercise 8: Sketch the graph of the surface and identify the surface in the space: [latex]\frac{x^{2}}{3^{2}}-\frac{y^{2}}{1^{2}}+\frac{z^{2}}{2^{2}}=1[/latex].
Example 9: Find the equation of the quadric surface with points [latex]P(x,y,z)[/latex] that are equidistant from point [latex]Q(-1,0,0)[/latex] and plane of equation [latex]x=2[/latex]. Identify the surface.
Example 10: Sketch the region bounded by cone [latex]x^{2}=y^{2}+z^{2}[/latex] and cylinder [latex]y^{2}+z^{2}=1[/latex] where [latex]0\leq x\leq2[/latex].
Group work:
1. Find the equation of the quadric surface with points [latex]P(x,y,z)[/latex] that are equidistant from point [latex]Q(0,0,-1)[/latex] and plane of equation [latex]z=1[/latex]. Identify the surface.
2. Determine the intersection points of parabolic hyperboloid [latex]z=3x^{2}-2y^{2}[/latex] with the line of parametric equations [latex]x=3t,y=2t,z=19t,[/latex] where [latex]t\in R.[/latex]
3. Sketch the region bounded by elliptic paraboloid [latex]x=y^{2}+z^{2}[/latex] and plane [latex]x+z=1[/latex].
4. Sketch the region inside the paraboloid [latex]x^{2}+y^{2}=z[/latex] and inside the sphere [latex]x^{2}+y^{2}+z^{2}=1[/latex].
5. Sketch the region bounded by [latex]y^{2}+z^{2}=4[/latex], [latex]x=0[/latex] and [latex]x+z=2[/latex].