Section 3.1 Functions of Several Variables

3.1 Functions of Several Variables

In this section, we learn the definition of functions of several variables. The goal is to understand the meaning of the function and its graph. The idea of defining a function with several variables is actually coming from daily life examples. The volume of a cylinder is depending on the height of the cylinder and the radius of the circular base. The temperature of the earth surface is depending on the location’s longitude and latitude.

Definition

A function of two variables [latex]z=f(x,y)[/latex] maps each ordered pair [latex](x,y)[/latex] in a subset [latex]D[/latex] of the real plane [latex]\mathbb{R}^{2}[/latex] to a unique real number [latex]z[/latex]. The set [latex]D[/latex] is called the domain of the function. The range of [latex]f[/latex] is the set of all real numbers [latex]z[/latex] that has at least one ordered pair [latex](x,y)[/latex] such that [latex]f(x,y)=z[/latex]. The variables [latex]x[/latex] and [latex]y[/latex] are independent variables and [latex]z[/latex] is the dependent variable. 

Example 1: Find the domain and range of the function [latex]f(x,y)=y+\sqrt{9-x^{2}}[/latex] and find [latex]f(1,2)[/latex]. Sketch the domain. 

Exercise 1: Find the domain and range of the function [latex]f(x,y)=x+\sqrt{4-y^{2}}[/latex] and find [latex]f(1,2)[/latex]. Sketch the domain. 

Example 2: Find the domain of the function [latex]f(x,y)=\frac{\sqrt{9-x^{2}-y^{2}}}{x-2}[/latex]. Sketch the domain. 

Exercise 2: Find the domain of the function [latex]f(x,y)=\frac{\text{ln}(x)}{\sqrt{4-x^{2}-y^{2}}}[/latex]. Sketch the domain. 

Recall in calculus I, when graphing a function [latex]y=f(x)[/latex] of one variable, we use the Cartesian plane. We are able to graph any ordered pair [latex](x,y)[/latex] in the plane, and every point in the plane has an ordered pair [latex](x,y)[/latex] associated with it. With a function of two variables, each ordered pair [latex](x,y)[/latex] in the domain of the function is mapped to a real number [latex]z[/latex]. Therefore, the graph of the function [latex]f[/latex] consists of ordered triples [latex](x,y,z)[/latex]. The graph of a function [latex]z=f(x,y)[/latex] of two variables is called a surface.

Example 3: Sketch the graph of [latex]f(x,y)=2x-y+2[/latex].

Exercise 3: Sketch the graph of [latex]f(x,y)=3x+2y-6[/latex].

Example 4: Sketch the graph of [latex]f(x,y)=2-x^{2}-y^{2}[/latex].

Exercise 4: Sketch the graph of [latex]f(x,y)=1+x^{2}+y^{2}[/latex].

Drawing a surface in the space is not easy especially if we want to describe it in more details. We introduce the idea of level curves which is very similar to the traces that are introduced earlier. 

Definition

Given a function [latex]f(x,y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two variables for the value [latex]c[/latex] is defined to be the set of points satisfying the equation [latex]f(x,y)=c[/latex]. The collection of level curves on the [latex]xy[/latex] plane is called the contour map of the function. 

Example 5: Draw the contour map of [latex]f(x,y)=\sqrt{4-x^{2}-4y^{2}}[/latex] for at least 4 levels. 

Exercise 5: Draw the contour map of [latex]f(x,y)=\sqrt{9-9x^{2}-y^{2}}[/latex] for at least 4 levels. 

We can define a function of one variable or two variables, hence it is naturally to ask if we can define a function of more variables.

Definition:

A function of [latex]n[/latex] variables, [latex]f[/latex], is a rule that assigns to each ordered triple [latex](x_{1},x_{2},x_{3},\cdots,x_{n})[/latex] in a domain [latex]D\subseteq\mathbb{R}^{n}[/latex] a unique real number denoted by [latex]f(x_{1},x_{2},x_{3},\cdots,x_{n})[/latex]. When there are [latex]3[/latex] variables, the surface [latex]c=f(x,y,z)[/latex] is called the level surface of the function. 

Example 6: Find the level surface for the function [latex]f(x,y,z)=x^{2}-y^{2}-z^{2}[/latex] at [latex]c=2[/latex] and describe it and draw it.

Exercise 6: Find the level surface for the function [latex]f(x,y,z)=x^{2}+y^{2}+z^{2}[/latex] at [latex]c=9[/latex] and describe it and draw it.

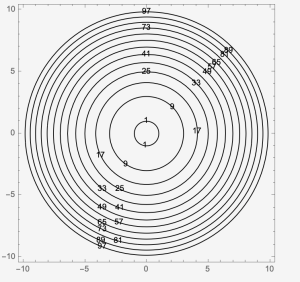
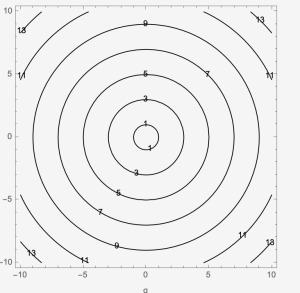
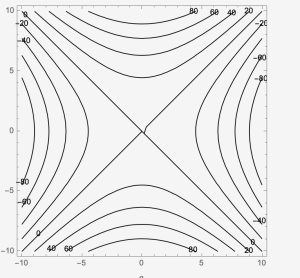
Example 7: Sketch [latex]f[/latex] where the contour map is given. What is the possible [latex]f(x,y)[/latex]?

Group work:

1. Sketch [latex]f[/latex] where the contour map is given. What is the possible [latex]f(x,y)[/latex]?

2. Sketch [latex]f[/latex] where the contour map is given. What is the possible [latex]f(x,y)[/latex]?

3. Find the level surface for the function [latex]f(x,y,z)=x^{2}-y^{2}-z^{2}[/latex] at [latex]c=2[/latex] and draw it.

4. Find the level surface for the function [latex]f(x,y,z)=x^{2}+y^{2}-z[/latex] at [latex]c=-4[/latex] and draw it.