Section 1.7 Quadric Surfaces
1.7 Quadric Surfaces
In this section, we introduce more equations of surfaces. We already learn two special type of surfaces, plane, [latex]ax+by+cz+d=0[/latex], and sphere, [latex](x-x_{1})^{2}+(y-y_{1})^{2}+(z-z_{1})^{2}=r^{2}[/latex]. Here we will learn cylinder and quadric surfaces. One of the most important way to recognize and describe those surface is the cross section of the surface and planes that are parallel to the coordinate planes. Those cross sections are curves and we call those cross sections traces. For example, the traces of a sphere are always circles and the traces of a plane are lines. One important goal for this section is recognizing and graphing those surfaces. Traces help us to archive this goal.
Definition: cylinder
A set of lines parallel to a given line passing through a given curve is known as a cylindrical surface, or cylinder. The parallel lines are called rulings.
Example 1: Sketch the graph of the surface in the space: [latex]x^{2}+z^{2}=1[/latex].
Exercise 1: Sketch the graph of the surface in the space: [latex]x^{2}+y^{2}=1[/latex].
Example 2: Sketch the graph of the surfaces in the space: [latex]z=y^{2}+1[/latex].
Exercise 2: Sketch the graph of the surface in the space: [latex]y=x^{2}[/latex].
Definition:
Quadric surfaces are the graphs of equations that can be expressed in the form
\[ Ax^{2}+By^{2}+Cz^{2}+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \]
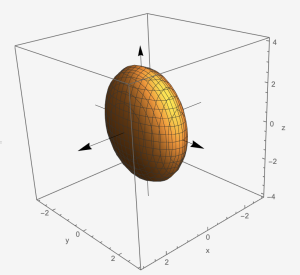
Example 3: Use traces to sketch the ellipsoid: [latex]\frac{x^{2}}{2^{2}}+\frac{y^{2}}{3^{2}}+\frac{z^{2}}{5^{2}}=1[/latex].
Exercise 3: Use traces to sketch the ellipsoid: [latex]\frac{x^{2}}{3^{2}}+\frac{y^{2}}{1^{2}}+\frac{z^{2}}{2^{2}}=1[/latex].
Example 4: Use traces to sketch the elliptic paraboloid: [latex]\frac{x^{2}}{2^{2}}-\frac{y}{3^{2}}+\frac{z^{2}}{5^{2}}=0[/latex].
Exercise 4: Use traces to sketch the elliptic paraboloid: [latex]\frac{x^{2}}{3^{2}}+\frac{y^{2}}{1^{2}}-\frac{z}{2^{2}}=0[/latex].
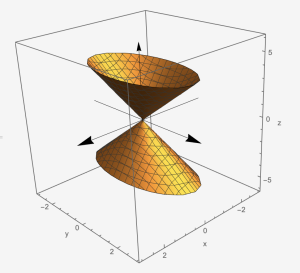
Example 5: Use traces to sketch the cone: [latex]\frac{x^{2}}{1^{1}}-\frac{y^{2}}{2^{2}}+\frac{z^{2}}{3^{2}}=0[/latex].
Exercise 5: Use traces to sketch the cone: [latex]\frac{x^{2}}{3^{2}}+\frac{y^{2}}{1^{2}}-\frac{z^{2}}{2^{2}}=0[/latex].
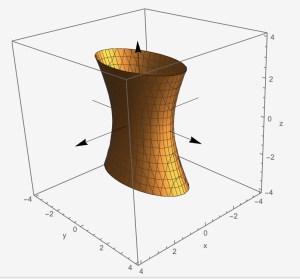
Example 6: Use traces to sketch the hyperboloid of one sheet: [latex]\frac{x^{2}}{1^{2}}-\frac{y^{2}}{2^{2}}+\frac{z^{2}}{3^{2}}=1[/latex].
Exercise 6: Use traces to sketch the hyperboloid of one sheet: [latex]\frac{x^{2}}{3^{2}}+\frac{y^{2}}{1^{2}}-\frac{z^{2}}{2^{2}}=1[/latex].
Common Quadratic Surfaces: Ellipsoid, Hyperboloid of One Sheet, Hyperboloid of Two Sheets, Cone, Elliptic Paraboloid, Hyperbolic Paraboloid.
Ellipsoid: [latex]\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1[/latex]
Hyperboloid of One Sheet: [latex]\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=1[/latex]
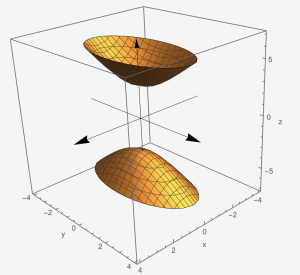
Hyperboloid of Two Sheets: [latex]-\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1[/latex]
Cone: [latex]\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=0[/latex]
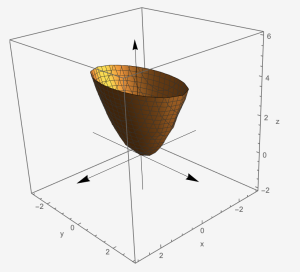
Elliptic Paraboloid: [latex]\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z}{c}=0[/latex]
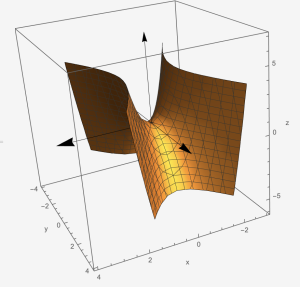
Hyperbolic Paraboloid: [latex]\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}-\frac{z}{c}=0[/latex]
Group work: Sketch the graph of the surface and identify the surface in space
1. [latex]\frac{x^{2}}{1^{2}}+\frac{y^{2}}{2^{2}}+\frac{z^{2}}{2^{2}}=1[/latex]
2. [latex]\frac{x^{2}}{2^{2}}+\frac{y^{2}}{3^{2}}-\frac{z^{2}}{1}=1[/latex]
3. [latex]\frac{x^{2}}{2^{2}}+\frac{y^{2}}{2^{2}}-z=0[/latex]
4. [latex]\frac{x^{2}}{2^{2}}+\frac{y^{2}}{2^{2}}-\frac{z^{2}}{2^{2}}=0[/latex]
5. [latex]-\frac{x^{2}}{2^{2}}-\frac{y^{2}}{2^{2}}+\frac{z^{2}}{2^{2}}=1[/latex]