Section 3.5 Chain Rules

3.5 Chain Rules

In this section, we learn the chain rule for the multi-variables function. Recall in calculus I, given a function [latex]y=f(g(t))=f(x),[/latex] with [latex]x=g(t)[/latex], then 

\[\frac{dy}{dt}=\frac{dy}{dx}\frac{dx}{dt}=f'(g(t))g'(t)\]

 if both [latex]y[/latex] and [latex]x[/latex] are differentiable. We use the similar approach for multi-variables but we need partial derivative because we can only take derivative at one direction at a time.

Theorem: Chain Rule for One Independent Variable

Suppose that [latex]x=g(t)[/latex] and [latex]y=h(t)[/latex] are differentiable functions of [latex]t[/latex] and [latex]z=f(x,y)[/latex] is a differentiable function of [latex]x[/latex] and [latex]y[/latex]. Then [latex]z=f(g(t),h(t))[/latex] is a differentiable function of [latex]t[/latex] and 

\[\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt}\]

where the ordinary derivatives are evaluated at [latex]t[/latex] and the partial derivatives are evaluated at [latex](x,y)[/latex].

Idea of the proof using the following equation:

\[z(t)=f(x,y)=f(x_{0},y_{0})+f_{x}(x_{0},y_{0})(x-x_{0})+f_{y}(x_{0},y_{0})(y-y_{0})+E(x,y),\]

Example 1: Find [latex]\frac{dz}{dt}[/latex], where [latex]z=f(x,y)=x^{2}y-xy^{2}+2x+y[/latex], [latex]x=x(t)=\text{sin}(t)[/latex], and [latex]y=y(t)=\text{cos}(t)[/latex]. 

Exercise 1: Find [latex]\frac{dz}{dt}[/latex], where [latex]z=f(x,y)=2x^{2}+x^{2}y-y^{3}[/latex], [latex]x=x(t)=\text{tan}(t)[/latex], and [latex]y=y(t)=\text{sec}(t)[/latex]. 

Example 2: Find [latex]\frac{dz}{dt}[/latex], where [latex]z=f(x,y)=\sqrt{x^{2}-y^{2}}[/latex], [latex]x=x(t)=e^{2t}[/latex], and [latex]y=y(t)=e^{t^{2}}[/latex]. 

Exercise 2: Find [latex]\frac{dz}{dt}[/latex], where [latex]z=f(x,y)=\sqrt{x^{2}+y^{2}}[/latex], [latex]x=x(t)=\text{ln}(t)[/latex], and [latex]y=y(t)=e^{-t}[/latex]. 

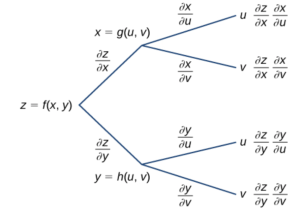
Theorem: Chain Rule for Two Independent Variables

Suppose [latex]x=g(u,v)[/latex] and [latex]y=h(u,v)[/latex] are differentiable functions of [latex]u[/latex] and [latex]v[/latex], and [latex]z=f(x,y)[/latex] is a differentiable function of [latex]x[/latex] and [latex]y[/latex]. Then, [latex]z=f(g(u,v),h(u,v))[/latex] is a differentiable function of [latex]u[/latex] and [latex]v[/latex]. Moreover,

\[\frac{\partial z}{\partial u}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial u}\]

and 

\[\frac{\partial z}{\partial v}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial v}.\]

Example 3: Find [latex]\frac{\partial z}{\partial u}[/latex] and [latex]\frac{\partial z}{\partial v},[/latex], where [latex]z=f(x,y)=3x^{3}-xy^{2}-y^{3}[/latex], [latex]x=x(u,v)=u^{2}+v[/latex], and [latex]y=y(u,v)=\text{ln}(u)+v[/latex]. 

Exercise 3: Find [latex]\frac{\partial z}{\partial u}[/latex] and [latex]\frac{\partial z}{\partial v},[/latex]where [latex]z=f(x,y)=x^{2}+xy+y^{2}[/latex], [latex]x=x(u,v)=3u+4v[/latex], and [latex]y=y(u,v)=2u-v[/latex]. 

Theorem Implicit Differentiation of a Function of Two or More Variables

Suppose the equation [latex]f(x,y)=0[/latex] defines [latex]y[/latex] implicitly as a differentiable function of [latex]x[/latex].  Then

\[\frac{dy}{dx}=-\frac{f_{x}(x,y)}{f_{y}(x,y)}\]

provided [latex]f_{y}(x,y)\neq0[/latex]. If the equation [latex]f(x,y,z)=0[/latex] defines [latex]z[/latex] implicitly as a differentiable function of [latex]x[/latex] and [latex]y[/latex], then 

\[\frac{\partial z}{\partial x}=-\frac{f_{x}(x,y,z)}{f_{z}(x,y,z)}\]

and 

\[\frac{\partial z}{\partial y}=-\frac{f_{y}(x,y,z)}{f_{z}(x,y,z)}\]

as long as [latex]f_{z}(x,y,z)\neq0[/latex]. 

Example 4: Calculate [latex]\frac{dy}{dx}[/latex] if [latex]y[/latex] is defined implicitly as a function of [latex]x[/latex] via the equation [latex]3x^{2}+2xy+y^{2}+5y-11=0[/latex]. What is the equation of the tangent line to the graph of this curve at point [latex](1,1)[/latex]?

Exercise 4: Calculate [latex]\frac{dy}{dx}[/latex] if [latex]y[/latex] is defined implicitly as a function of [latex]x[/latex] via the equation [latex]x^{2}-3xy+2y^{2}+5x-1=0[/latex]. What is the equation of the tangent line to the graph of this curve at point [latex](-1,1)[/latex]?

Example 5: Calculate [latex]\frac{\partial z}{\partial x}[/latex] and [latex]\frac{\partial z}{\partial y}[/latex], given [latex]x^{2}e^{y}-yze^{x}=0[/latex].

Exercise 5: Calculate [latex]\frac{\partial z}{\partial x}[/latex] and [latex]\frac{\partial z}{\partial y}[/latex], given [latex]ye^{x}+\text{ln}(x)z^{2}=0[/latex].

Example 6: The volume of a right circular cylinder is given by [latex]V(x,y)=\pi x^{2}y[/latex], where [latex]x[/latex] is the radius of the cylinder and [latex]y[/latex] is the cylinder height. Suppose [latex]x[/latex] and [latex]y[/latex] are functions of [latex]t[/latex] given by [latex]x=\frac{1}{3}t[/latex] and [latex]y=t[/latex] so that [latex]x[/latex] and [latex]y[/latex] are both increasing with time. How fast is the volume increasing when [latex]x=3[/latex] and [latex]y=4[/latex]?

Example 7: A closed box is in the shape of a rectangular solid with dimensions [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex]. (Dimensions are in inches.) Suppose each dimension is changing at the rate of [latex]0.4[/latex] in./min. Find the rate of change of the total surface area of the box when [latex]x=2[/latex] in., [latex]y=2[/latex] in., and [latex]z=1[/latex] in.

Group work:

1. The volume of a right circular cone is given by [latex]V(x,y)=\frac{1}{3}\pi x^{2}y[/latex], where [latex]x[/latex] is the radius of the base and [latex]y[/latex] is the height of the cone. Suppose [latex]x[/latex] and [latex]y[/latex] are functions of [latex]t[/latex] given by [latex]x=\frac{1}{2}t[/latex] and [latex]y=2t[/latex] so that [latex]x[/latex] and [latex]y[/latex] are both increasing with time. How fast is the volume increasing when [latex]x=2[/latex] and [latex]y=8[/latex]?

2. A closed box is in the shape of a rectangular solid with dimensions [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex]. (Dimensions are in inches.) Suppose each dimension is changing at the rate of [latex]0.3[/latex] in./min. Find the rate of change of the total surface area of the box when [latex]x=1[/latex] in., [latex]y=2[/latex] in., and [latex]z=3[/latex] in.

3. The [latex]x[/latex] and [latex]y[/latex] components of a fluid moving in two dimensions are given by the following functions: [latex]u(x,y)=2y[/latex] and [latex]v(x,y)=-2x[/latex]; [latex]x\ge0;y\ge0[/latex]. The speed of the fluid at the point [latex](x,y)[/latex] is [latex]s(x,y)=u(x,y)^{2}+v(x,y)^{2}[/latex]. Find [latex]\frac{\partial s}{\partial x}[/latex] and [latex]\frac{\partial s}{\partial y}[/latex] using the chain rule.

4. Let [latex]u=u(x,y,z)[/latex], where [latex]x=x(w,t)[/latex], [latex]y=y(w,t)[/latex], [latex]z=z(w,t)[/latex], [latex]w=w(r,s)[/latex], and [latex]t=t(r,s)[/latex]. Use a tree diagram and the chain rule to find an expression for [latex]\frac{\partial u}{\partial r}[/latex].