Section 3.7 Maxima and Minima

3.7 Maxima and Minima

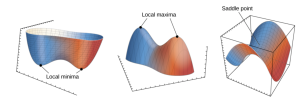
In calculus I, the most useful application for taking derivative of a function is finding the maximum and the minimum of the function. In this section, we learn how to find maxima or minima of a two variables function. First, we define what does it mean to have a maximum or a minimum at a point for a two variable function.

Definition: 

Let [latex]z=f(x,y)[/latex] be a function of two variables that is defined and continuous on an open set containing the point [latex](x_{0},y_{0})[/latex]. Then [latex]f[/latex] has a local maximum (local minimum) at [latex](x_{0},y_{0})[/latex] if 

\[{\color{red}f(x_{0},y_{0})\geq f(x,y)},\text{ }({\color{blue}f(x_{0},y_{0})\leq f(x,y)})\]

for all points [latex](x,y)[/latex] within some disk centered at [latex](x_{0},y_{0})[/latex]. The number [latex]f(x_{0},y_{0})[/latex] is called a local maximum value (local minimum value). If the preceding inequality holds for every point [latex](x,y)[/latex] in the domain of [latex]f[/latex] , then [latex]f[/latex] has a global maximum/absolute maximum (global minimum/absolute minimum) at [latex](x_{0},y_{0})[/latex]. 

Definition: critical point 

Let [latex]z=f(x,y)[/latex] be a function of two variables that is defined on an open set containing the point [latex](x_{0},y_{0})[/latex]. The point [latex](x_{0},y_{0})[/latex] is called a critical point of a function of two variables [latex]f[/latex] if one of the two following conditions holds: 

1. [latex]f_{x}(x_{0},y_{0})=f_{y}(x_{0},y_{0})=0[/latex] 

2. Either [latex]f_{x}(x_{0},y_{0})[/latex] or [latex]f_{y}(x_{0},y_{0})[/latex] does not exist.

Example 1: Find the critical points of the functions: [latex]z=f(x,y)=x^{2}+xy+y^{2}+y+4[/latex]. 

Exercise 1: Find the critical points of the functions: [latex]z=f(x,y)=x^{2}-3xy+y^{2}+3y+1[/latex]. 

Theorem: Fermat\textquoteright s Theorem for Functions of Two Variables

Let [latex]z=f(x,y)[/latex] be a function of two variables that is defined and continuous on an open set containing the point [latex](x_{0},y_{0})[/latex]. Suppose [latex]f_{x}[/latex] and [latex]f_{y}[/latex] each exists at [latex](x_{0},y_{0})[/latex]. If [latex]f[/latex] has a local extremum at [latex](x_{0},y_{0})[/latex], then [latex](x_{0},y_{0})[/latex] is a critical point of [latex]f[/latex]. 

Definition: Given the function [latex]z=f(x,y)[/latex], the point [latex](x_{0},y_{0},f(x_{0},y_{0}))[/latex] is a saddle point if both [latex]f_{x}(x_{0},y_{0})=f_{y}(x_{0},y_{0})=0[/latex], but [latex]f[/latex] does not have a local extremum at [latex](x_{0},y_{0})[/latex].

Theorem: Second Derivative Test 

Let [latex]z=f(x,y)[/latex] be a function of two variables for which the first- and second-order partial derivatives are continuous on some disk containing the point [latex](x_{0},y_{0})[/latex]. Suppose [latex]f_{x}(x_{0},y_{0})=f_{y}(x_{0},y_{0})=0[/latex].

Define the quantity

\[D=f_{xx}(x_{0},y_{0})f_{yy}(x_{0},y_{0})-(f_{xy}(x_{0},y_{0}))^{2}.\]

i. If [latex]D\gt 0[/latex] and [latex]f_{xx}(x_{0},y_{0})\gt 0[/latex], then [latex]f[/latex] has a local minimum at [latex](x_{0},y_{0})[/latex]. 

ii. If [latex]D\gt 0[/latex] and [latex]f_{xx}(x_{0},y_{0})\lt 0[/latex], then [latex]f[/latex] has a local maximum at [latex](x_{0},y_{0})[/latex]. 

iii. If [latex]D\lt 0[/latex], , then [latex]f[/latex] has a saddle point at [latex](x_{0},y_{0})[/latex].

iv. If [latex]D=0[/latex], then the test is inconclusive.

Example 2: Find the critical points of the function [latex]f(x,y)=x^{2}+3y^{2}+2x-12y+4[/latex], and use the second derivative test to find the local extrema.

Exercise 2: Find the critical points of the function [latex]f(x,y)=2x^{2}-y^{2}+12x+8y-3[/latex], and use the second derivative test to find the local extrema.

Example 3: Find the critical points of the function [latex]f(x,y)=\frac{1}{3}x^{3}+y^{2}+2xy-6x-3y+4[/latex], and use the second derivative test to find the local extrema.

Exercise 3: Find the critical points of the function [latex]f(x,y)=x^{3}+4xy-8x-4y^{2}[/latex], and use the second derivative test to find the local extrema.

Theorem: Extreme Value Theorem 

A continuous function [latex]f(x,y)[/latex] on a closed and bounded set [latex]D[/latex] in the plane attains an absolute maximum value at some point of [latex]D[/latex] and an absolute minimum value at some point of [latex]D[/latex].

Theorem: Finding Extreme Values of a Function of Two Variables 

Assume [latex]z=f(x,y)[/latex] is a differentiable function of two variables defined on a closed, bounded set [latex]D[/latex]. Then [latex]f[/latex] will attain the absolute maximum value and the absolute minimum value, which are, respectively, the largest and smallest values found among the following: 

i. The values of [latex]f[/latex] at the critical points of [latex]f[/latex] in [latex]D[/latex]. 

ii. The values of [latex]f[/latex] on the boundary of [latex]D[/latex].

Example 4: Find absolute extrema of the function [latex]f(x,y)=x^{2}+2y^{2}-4x-4y+2[/latex] on the domain defined by [latex]0\leq x\leq 4[/latex] and [latex]-2\leq y\leq 2[/latex].

Exercise 4: Find absolute extrema of the function [latex]f(x,y)=4x^{2}+y^{2}-8x+2y+3[/latex] on the domain defined by [latex]0\leq x\leq 2[/latex] and [latex]-1\leq y\leq 3[/latex].

Example 5: Find absolute extrema of the function [latex]f(x,y)=x^{2}+y^{2}-2x+4y[/latex] on the range [latex]R=\{(x,y)|x^{2}+y^{2}\leq9\}.[/latex]

Exercise 5: Find absolute extrema of the function [latex]f(x,y)=x^{2}+y^{2}-2y+1[/latex] on the range [latex]R=\{(x,y)|x^{2}+y^{2}\leq4\}.[/latex]

Group work:

1. Find absolute extrema of the function [latex]f(x,y)=10-6x+x^{2}-4y+y^{2}[/latex] on the range [latex]R[/latex] is the triangular region with vertices [latex](0,0),(4,0),[/latex] and [latex](4,4)[/latex].

2. Find absolute extrema of the function [latex]f(x,y)=x^{2}y^{2}[/latex] on the range [latex]R=\{(x,y)|x\geq0,x^{2}+y^{2}\leq4\}.[/latex]

3. Find the critical points of the function [latex]f(x,y)=x^{3}+y^{3}-300x-75y-3[/latex], and use the second derivative test to find the local extrema.

4. Find absolute extrema of the function [latex]f(x,y)=3x^{2}-2xy+y^{2}-8y[/latex] on the domain defined by [latex]-2\leq x\leq2[/latex] and [latex]0\leq y\leq4[/latex].

5. Find absolute extrema of the function [latex]f(x,y)=(x-2)^{2}+(y-4)^{2}[/latex] on the range [latex]R[/latex] is the triangular region with vertices [latex](0,0),(4,0),[/latex] and [latex](0,4)[/latex].