Section 4.6 Spherical Integral
4.6 Spherical Integral
Recall the Spherical Coordinates system denotes a point in a 3-dimensional space via [latex](\rho,\theta,\varphi)[/latex] where [latex]\rho[/latex] is the distance between the point and origin, [latex]\theta[/latex] is the angle between the point and positive [latex]x[/latex]-axis, and [latex]\varphi[/latex] is the angle between the point and positive [latex]z[/latex]-axis. Hence we have relationships,
\[x^{2}+y^{2}+z^{2}=\rho^{2},\text{ }x=\rho\text{sin}(\varphi)\text{cos}(\theta),\text{ }y=\rho\text{sin}(\varphi)\text{sin}(\theta),\text{}z=\rho\text{cos}(\varphi).\]
Definition: Triple Integrals
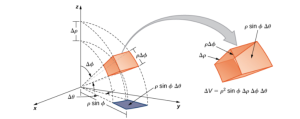
Consider the spherical box (expressed in spherical coordinates) \[B=\{(\rho,\theta,\varphi)|a\le\rho\le b,\alpha\le\theta\le\beta,c\le\varphi\le d\}.\]
If the function [latex]f(\rho,\theta,\varphi)[/latex] is continuous on [latex]B[/latex] and if [latex](\rho_{ijk}^{*},\theta_{ijk}^{*},\varphi_{ijk}^{*})[/latex] is any sample point in the spherical [latex]B_{ijk}=[\rho_{i-1},\rho_{i}]\times[\theta_{j-1},\theta_{j}]\times[\varphi_{k-1},\varphi_{k}][/latex], then we can define the triple integral in spherical coordinates as the limit of a triple Riemann sum, provided the following limit exist
\[ \lim_{l,m,n\rightarrow\infty}\sum_{i=1}^{l}\sum_{j=1}^{m}\sum_{k=1}^{n}f(\rho_{ijk}^{*},\theta_{ijk}^{*},\varphi_{ijk}^{*})(\rho_{ijk}^{*})^{2}\text{sin}(\varphi)\triangle\rho\triangle\theta\triangle\varphi \]
if the limit exists.
Theorem: Fubini' s Theorem in Cylindrical Coordinates
Suppose that [latex]g(x,y,z)[/latex] is continuous on a box B, which when described in spherical coordinates looks like [latex]B=\{(\rho,\theta,\varphi)|a\le\rho\le b,\alpha\le\theta\le\beta,c\le\varphi\le d\}[/latex].
Then [latex]g(x,y,z)=g(\rho\text{sin}(\varphi)\text{cos}(\theta),\rho\text{sin}(\varphi)\text{sin}(\theta),\rho\text{cos}(\varphi))=f(\rho,\theta,\varphi)[/latex] and
\[\int\int\int_{B}g(x,y,z)dV=\int_{c}^{d}\int_{\alpha}^{\beta}\int_{a}^{b}f(\rho,\theta,\varphi)\rho^{2}\text{sin}(\varphi)d\rho d\theta d\varphi.\]
This iterated integral may be replaced by other iterated integrals by integrating with respect to the three variables in other orders.
Example 1: Evaluating the triple integral [latex]\int_{0}^{\pi}\int_{0}^{\frac{\pi}{2}}\int_{0}^{1}\rho^{2}\text{sin}(\varphi)d\rho d\theta d\varphi[/latex].
Exercise 1: Evaluating the triple integral [latex]\int_{0}^{\frac{\pi}{2}}\int_{0}^{\pi}\int_{0}^{2}\rho^{2}\text{sin}(\varphi)d\rho d\theta d\varphi[/latex].
Remark (Theorem): As before, we can do the integration over a general box, not just a spherical one.
Example 2: Let [latex]E[/latex] be the region bounded above by the cone [latex]z=-\sqrt{x^{2}+y^{2}}[/latex] and below by the sphere [latex]z^{2}+x^{2}+y^{2}=1[/latex] . Set up a triple integral in spherical coordinates to find the volume of the region.
Exercise 2: Let [latex]E[/latex] be the region bounded below by the cone [latex]z=\sqrt{3x^{2}+3y^{2}}[/latex] and above by the sphere [latex]z^{2}+x^{2}+y^{2}=4[/latex] . Set up a triple integral in spherical coordinates to find the volume of the region.
Example 3: Sketch the solid whose volume is given by the integral and evaluate the integral [latex]\int_{0}^{\frac{\pi}{6}}\int_{0}^{\frac{\pi}{3}}\int_{0}^{1}\rho^{2}\text{sin}(\varphi)d\rho d\theta d\varphi[/latex].
Exercise 3: Sketch the solid whose volume is given by the integral and evaluate the integral [latex]\int_{0}^{\frac{\pi}{4}}\int_{0}^{\pi}\int_{0}^{2}\rho^{2}\text{sin}(\varphi)d\rho d\theta d\varphi[/latex].
Example 4: Sketch the solid whose volume is given by the integral and evaluate the integral [latex]\int_{0}^{\frac{\pi}{6}}\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\text{sec}(\varphi)}\rho^{2}\text{sin}(\varphi)d\rho d\theta d\varphi[/latex].
Exercise 4: Sketch the solid whose volume is given by the integral and evaluate the integral [latex]\int_{0}^{\frac{\pi}{4}}\int_{0}^{\frac{\pi}{3}}\int_{0}^{\text{sec}(\varphi)}\rho^{2}\text{sin}(\varphi)d\rho d\theta d\varphi[/latex].
Example 5: Sketch the solid. Evaluating the triple integral [latex]\int\int\int_{E}xdV[/latex] where [latex]E[/latex] is the solid of hemisphere [latex]x^{2}+y^{2}+z^{2}\leq4[/latex], [latex]x\geq0[/latex].
Exercise 5: Sketch the solid. Evaluating the triple integral [latex]\int\int\int_{E}ydV[/latex] where [latex]E[/latex] is the solid of hemisphere [latex]x^{2}+y^{2}+z^{2}\leq9[/latex], [latex]y\geq0[/latex].
Example 6: Sketch the solid and find its volume. The solid lies inside both of sphere [latex]x^{2}+y^{2}+z^{2}=4[/latex], and the cone [latex]\sqrt{x^{2}+y^{2}}=z[/latex].
Exercise 6: Sketch the solid and find its volume. The solid lies inside sphere [latex]x^{2}+y^{2}+z^{2}=9[/latex], and outside the cone [latex]\sqrt{x^{2}+y^{2}}=z[/latex].
Example 7: Sketch the solid and find its volume. The solid lies above the cone [latex]\varphi=\frac{\pi}{3}[/latex] and below the sphere [latex]\rho=4\text{cos}(\varphi)[/latex]
Example 8: Change the integration into spherical coordinates
\[\int_{0}^{1}\int_{0}^{\sqrt{1-x^{2}}}\int_{\sqrt{x^{2}+y^{2}}}^{\sqrt{2-x^{2}-y^{2}}}xzdzdydx\]
Group work:
1. Sketch the solid and find its volume. The solid lies above the cone [latex]\varphi=\frac{\pi}{4}[/latex] and below the sphere [latex]\rho=6\text{cos}(\varphi)[/latex].
2. Change the integration into spherical coordinates
\[\int_{-4}^{4}\int_{0}^{\sqrt{16-x^{2}}}\int_{-\sqrt{16-x^{2}-y^{2}}}^{\sqrt{16-x^{2}-y^{2}}}x^{2}+y^{2}dzdydx.\]
3. Sketch the solid and find its volume. The solid lies inside between the spheres [latex]x^{2}+y^{2}+z^{2}=4[/latex] and [latex]x^{2}+y^{2}+z^{2}=1[/latex] and above the cone [latex]z=\sqrt{x^{2}+y^{2}}[/latex].
4. Sketch the solid and find its volume. The solid is obtained by cutting out a smaller wedge from a sphere of radius 4 by two planes intersect along a diameter at an angle of [latex]\frac{\pi}{3}[/latex].