Section 5.7. Classify Phase planes

Objective:

Classify Phase planes with eigenvalues

In this section, we are going to summarize all cases that we considered and classify all phase planes. Recall that a given matrix $A$ and a system of homogeneous differential equation $\overrightarrow{X}=A\overrightarrow{x}$, we can find the eigenvalues of the matrix $A$ and then eigenvectors. $\text{det}(A-\lambda I)=0=f(\lambda ),$ the characteristics equation determinate the eigenvalues. 

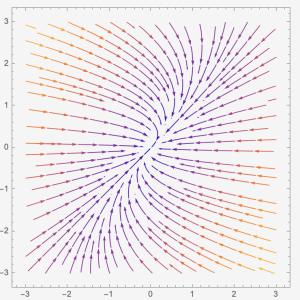
Case 1: When $f(\lambda )=0$ has two distinct positive real solutions, ${\lambda }_1>{\lambda }_2>0$. In this case, we have two eigenvectors, $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$. The entries of $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$ are real numbers. The general solution will be $\overrightarrow{x(t)}=c_1{e}^{{\lambda }_{1}t}\overrightarrow{v_1}+c_2{e}^{{\lambda }_{2}t}\overrightarrow{v_2}$. The phase plane has two straight lines such that they present the eigenvector directions. The arrows are pointing away from the $(0,0)$. The $\overrightarrow{x}=\overrightarrow{0}$ is called a nodal source and is an unstable solution. 

Case 2: When $f(\lambda )=0$ has two distinct negative real solutions, ${\lambda }_1<{\lambda }_2<0$. }In this case, we have two eigenvectors, $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$. The entries of $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$ are real numbers. The general solution will be $\overrightarrow{x(t)}=c_1{e}^{{\lambda }_{1}t}\overrightarrow{v_1}+c_2{e}^{{\lambda }_{2}t}\overrightarrow{v_2}$. The phase plane has two straight lines such that they present the eigenvector directions. The arrows are pointing toward the $(0,0)$. The $\overrightarrow{x}=\overrightarrow{0}$ is called a nodal sink and is a stable solution. 

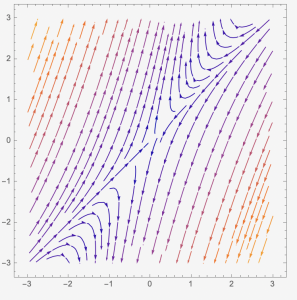
Case 3: When $f(\lambda )=0$ has two distinct real solutions, one is positive and one is negative, ${\lambda }_1<0<{\lambda }_2$}. In this case, we have two eigenvectors, $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$. The entries of $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$ are real numbers. The general solution will be $\overrightarrow{x(t)}=c_1{e}^{{\lambda }_{1}t}\overrightarrow{v_1}+c_2{e}^{{\lambda }_{2}t}\overrightarrow{v_2}$. The phase plane has two straight lines such that they present the eigenvector directions. The arrow on $\overrightarrow{v_1}$ is pointing toward the $(0,0)$, and the arrow on $\overrightarrow{v_2}$ is pointing away from $(0,0)$. The $\overrightarrow{x}=\overrightarrow{0}$ is called a saddle point and is an unstable solution.

Example 1: Given $\left[\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right]=\left[\begin{array}{cc}-4& -4\\ 0& -1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=A\overrightarrow{x}$, find the general solution of the system of equations. Classify the stability of the equilibrium solution $\overrightarrow{x}=\overrightarrow{0}$ and describe what kind of critical point it is. 

Exercise 1: Given $\left[\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right]=\left[\begin{array}{cc}-2& 0\\ 3& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=A\overrightarrow{x}$, find the general solution of the system of equations. Classify the stability of the equilibrium solution $\overrightarrow{x}=\overrightarrow{0}$ and describe what kind of critical point it is. 

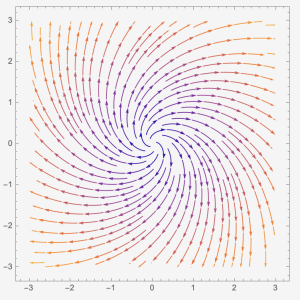
Case 4: When $f(\lambda )=0$ has two distinct complex solutions, $\lambda =a\pm bi$ and $a\ne 0$. In this case, we have two eigenvectors, $\overrightarrow{v_1}=\overrightarrow{p}+i\overrightarrow{q}$ and $\overrightarrow{v_2}=\overrightarrow{p}-i\overrightarrow{q}$. The entries of $\overrightarrow{p}$ and $\overrightarrow{q}$ are real numbers. The general solution will be $\overrightarrow{x(t)}=e^{at}(c_1(\text{cos}(bt)\overrightarrow{p}-\text{sin}(bt)\overrightarrow{q})+c_2(\text{sin}(bt)\overrightarrow{p}+\text{cos}(bt)\overrightarrow{q}))$. The entries of the vector $\overrightarrow{x(t)}$ have $\text{cos}(bt)$ and $\text{sin}(bt)$. The phase plane has clock-wise spiral orientations. The arrows on are pointing toward the $(0,0)$ if $a<0$, and the arrows are pointing away from $(0,0)$ if $a>0$. The $\overrightarrow{x}=\overrightarrow{0}$ is called a spiral sink and is a stable solution for $a<0$ case, and is called a spiral source and is an unstable solution for $a>0$ case.

Example 2: Given $\left[\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right]=\left[\begin{array}{cc}-1& 2\\ -2& -1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=A\overrightarrow{x}$, find the general solution of the system of equations. Classify the stability of the equilibrium solution $\overrightarrow{x}=\overrightarrow{0}$ and describe what kind of critical point it is. 

Exercise 2: Given $\left[\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right]=\left[\begin{array}{cc}2& -3\\ 3& 2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=A\overrightarrow{x}$, find the general solution of the system of equations. Classify the stability of the equilibrium solution $\overrightarrow{x}=\overrightarrow{0}$ and describe what kind of critical point it is. 

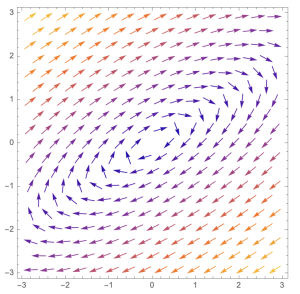
Case 5: When $f(\lambda )=0$ has  two distinct complex solutions, $\lambda =\pm bi$.} In this case, we have two eigenvectors, $\overrightarrow{v_1}=\overrightarrow{p}+i\overrightarrow{q}$ and $\overrightarrow{v_2}=\overrightarrow{p}-i\overrightarrow{q}$. The general solution will be $\overrightarrow{x(t)}=(c_1(\text{cos}(bt)\overrightarrow{p}-\text{sin}(bt)\overrightarrow{q})+c_2(\text{sin}(bt)\overrightarrow{p}+\text{cos}(bt)\overrightarrow{q}))$. The entries of the vector $\overrightarrow{x(t)}$ have $\text{cos}(bt)$ and $\text{sin}(bt)$. The phase plane has counter-clock-wise or clock-wise circular ( ellipse) orientations. The arrows counter-clock-wise or counter-clock-wise. The $\overrightarrow{x}=\overrightarrow{0}$ is called center and is a (neutrally) stable solution. 

Example 3: Given $\left[\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right]=\left[\begin{array}{cc}2& -4\\ 2& -2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=A\overrightarrow{x}$, find the general solution of the system of equations. Classify the stability of the equilibrium solution $\overrightarrow{x}=\overrightarrow{0}$ and describe what kind of critical point it is. 

Exercise 3: Given $\left[\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right]=\left[\begin{array}{cc}-3& -5\\ 2& 3\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=A\overrightarrow{x}$, find the general solution of the system of equations. Classify the stability of the equilibrium solution $\overrightarrow{x}=\overrightarrow{0}$ and describe what kind of critical point it is. 

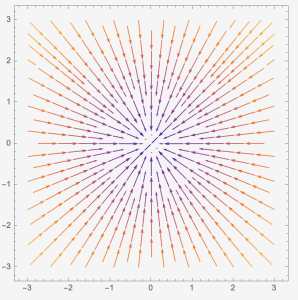
Case 6: When $f(\lambda )=0$ has one real solution, ${\lambda }_1$, and two eigenvectors, $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$. }The entries of $\overrightarrow{v_1}$ and $\overrightarrow{v_2}$ are real numbers. The general solution will be $\overrightarrow{x(t)}=c_1{e}^{{\lambda }_{1}t}\overrightarrow{v_1}+c_2{e}^{{\lambda }_{1}t}\overrightarrow{v_2}$. The phase plane has straight lines passing $(0,0)$. The arrow those lines are pointing toward the $(0,0)$ if ${\lambda }_1<0$, and the arrows are pointing away from $(0,0)$ if ${\lambda }_1>0$. The $\overrightarrow{x}=\overrightarrow{0}$ is called a star node, sometimes is called proper node. It is a stable solution if [latex]\lambda_{1} \lt 0,[/latex] and an unstable solution if ${\lambda }_1>0$.

Example 4: Given $\left[\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right]=\left[\begin{array}{cc}2& 0\\ 0& 2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=A\overrightarrow{x}$, find the general solution of the system of equations. Classify the stability of the equilibrium solution $\overrightarrow{x}=\overrightarrow{0}$ and describe what kind of critical point it is. 

Exercise 4: Given $\left[\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right]=\left[\begin{array}{cc}-3& 0\\ 0& -3\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=A\overrightarrow{x}$, find the general solution of the system of equations. Classify the stability of the equilibrium solution $\overrightarrow{x}=\overrightarrow{0}$ and describe what kind of critical point it is. 

Case 7: When $f(\lambda )=0$ has one real solution, ${\lambda }_1$, and one eigenvector, $\overrightarrow{v}$. The entries of $\overrightarrow{v}$ are real numbers. The general solution will be $\overrightarrow{x(t)}=c_1{e}^{{\lambda }_{1}t}\overrightarrow{v}+c_2[e^{{\lambda }_{1}t}\overrightarrow{w}+e^{{\lambda }_{1}t}t\overrightarrow{v}]$ where $(A-{\lambda }_1)\overrightarrow{w}=\overrightarrow{v}$. The phase plane has one straight line passing $(0,0)$. The arrow those lines are pointing toward the $(0,0)$ if ${\lambda }_1<0$, and the arrows are pointing away from $(0,0)$ if ${\lambda }_1>0$. The $\overrightarrow{x}=\overrightarrow{0}$ is called an improper node. It is a stable solution if ${\lambda }_1<0,$ and an unstable solution if ${\lambda }_1>0$.

Example 5: Given $\left[\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right]=\left[\begin{array}{cc}2& 3\\ 0& 2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=A\overrightarrow{x}$, find the general solution of the system of equations. Classify the stability of the equilibrium solution $\overrightarrow{x}=\overrightarrow{0}$ and describe what kind of critical point it is. 

Exercise 5: Given $\left[\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right]=\left[\begin{array}{cc}-3& 0\\ 2& -3\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=A\overrightarrow{x}$, find the general solution of the system of equations. Classify the stability of the equilibrium solution $\overrightarrow{x}=\overrightarrow{0}$ and describe what kind of critical point it is.