4.4 Silicate Minerals
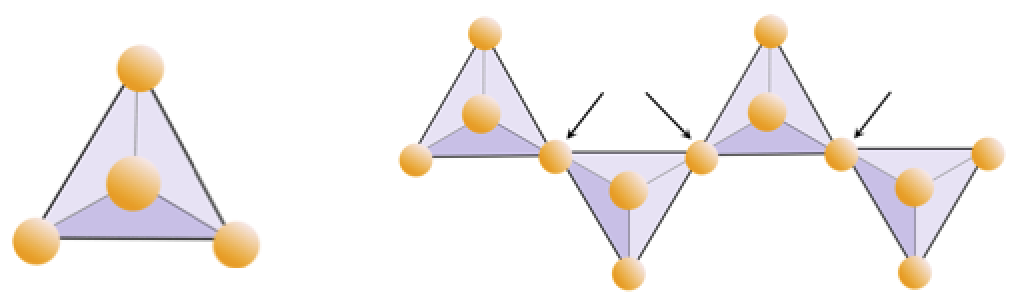
The vast majority of the minerals that make up the rocks of Earth’s crust are silicate minerals. These include minerals such as quartz, feldspar, mica, amphibole, pyroxene, olivine, and a great variety of clay minerals. The building block of all of these minerals is the silica tetrahedron, a combination of four oxygen atoms and one silicon atom. These are arranged such that planes drawn through the oxygen atoms form a tetrahedron (Figure 4.6). Since the silicon ion has a charge of +4 and each of the four oxygen ions has a charge of –2, the silica tetrahedron has a net charge of –4.
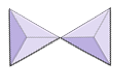
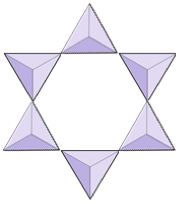
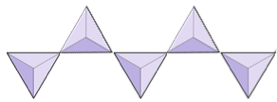
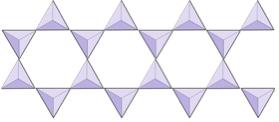
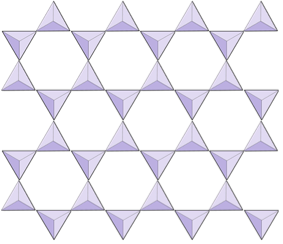
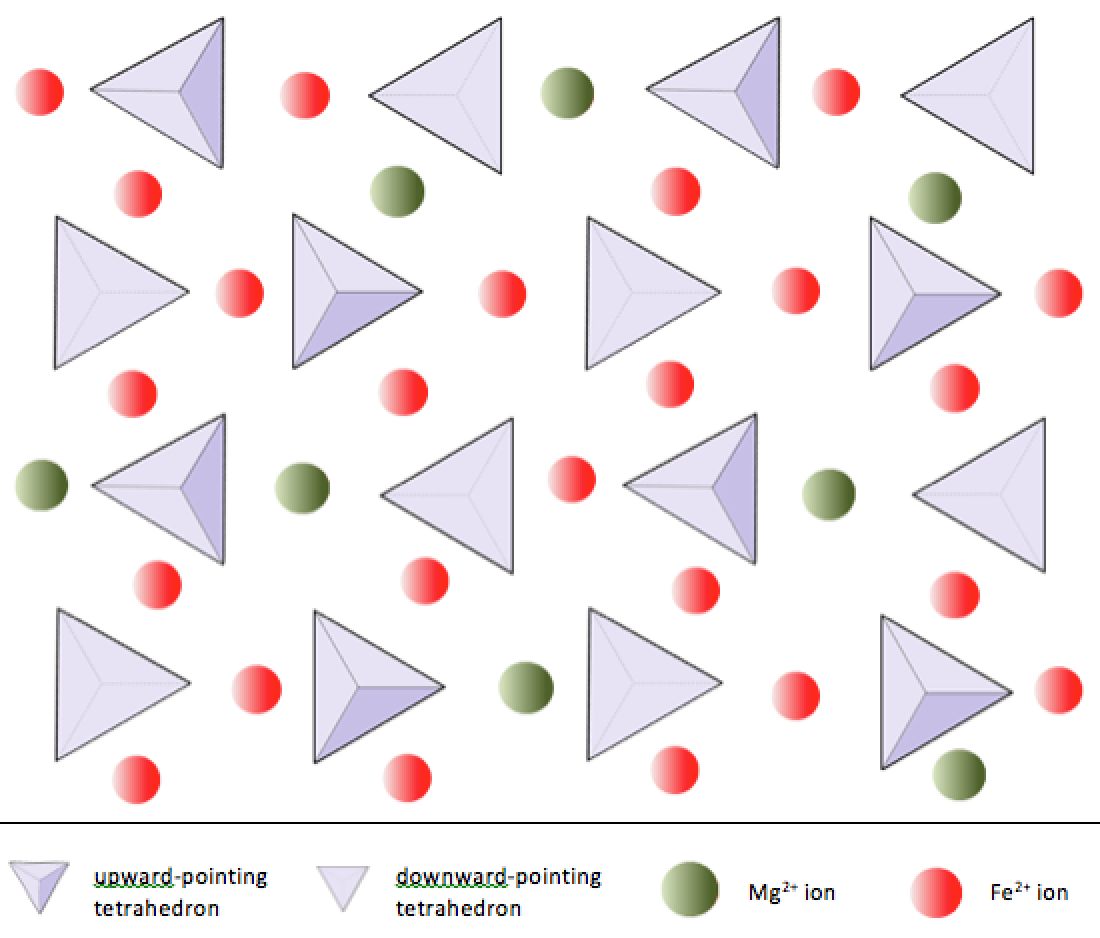
In silicate minerals, these tetrahedra are arranged and linked together in a variety of ways, from single units to complex frameworks (Figure 4.9). The simplest silicate structure, that of the mineral olivine, is composed of isolated tetrahedra bonded to iron and/or magnesium ions. In olivine, the –4 charge of each silica tetrahedron is balanced by two divalent (i.e., +2) iron or magnesium cations. Olivine can be either Mg2SiO4 or Fe2SiO4, or some combination of the two (Mg,Fe)2SiO4. The divalent cations of magnesium and iron are quite close in radius (0.73 versus 0.62 angstroms[1]). Because of this size similarity, and because they are both divalent cations (both have a charge of +2), iron and magnesium can readily substitute for each other in olivine and in many other minerals.
Figure 4.9 Silicate mineral configurations. The triangles represent silica tetrahedra.
Exercises
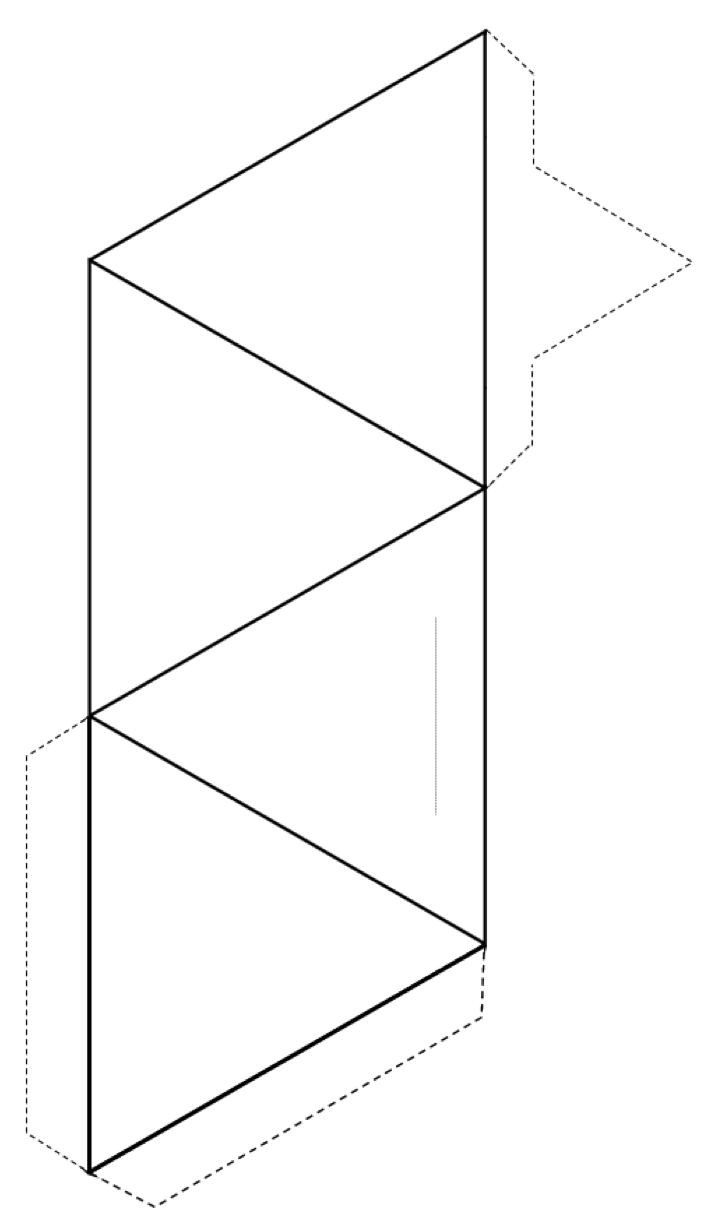
Exercise 4.3 Make a Tetrahedron
Cut around the outside of the shape (solid lines and dotted lines), and then fold along the solid lines to form a tetrahedron.
If you have glue or tape, secure the tabs to the tetrahedron to hold it together. If you don’t have glue or tape, make a slice along the thin grey line and insert the pointed tab into the slit.
If you are doing this in a classroom, try joining your tetrahedron with others into pairs, rings, single and double chains, sheets, and even three-dimensional frameworks.
In olivine, unlike most other silicate minerals, the silica tetrahedra are not bonded to each other. They are, however, bonded to the iron and/or magnesium as shown on Figure 2.10.
As already noted, the +2 ions of iron and magnesium are similar in size (although not quite the same). This allows them to substitute for each other in some silicate minerals. In fact, the common ions in silicate minerals have a wide range of sizes, as shown in Figure 4.11. All of the ions shown are cations, except for oxygen. Note that iron can exist as both a +2 ion (if it loses two electrons during ionization) or a +3 ion (if it loses three). Fe2+ is known as ferrous iron. Fe3+ is known as ferric iron. Ionic radii are critical to the composition of silicate minerals, so we’ll be referring to this diagram again.

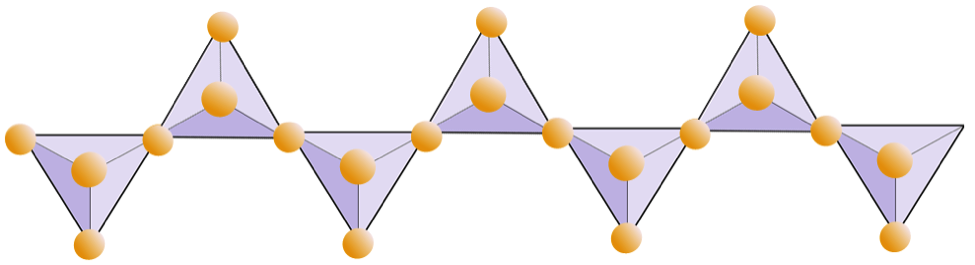
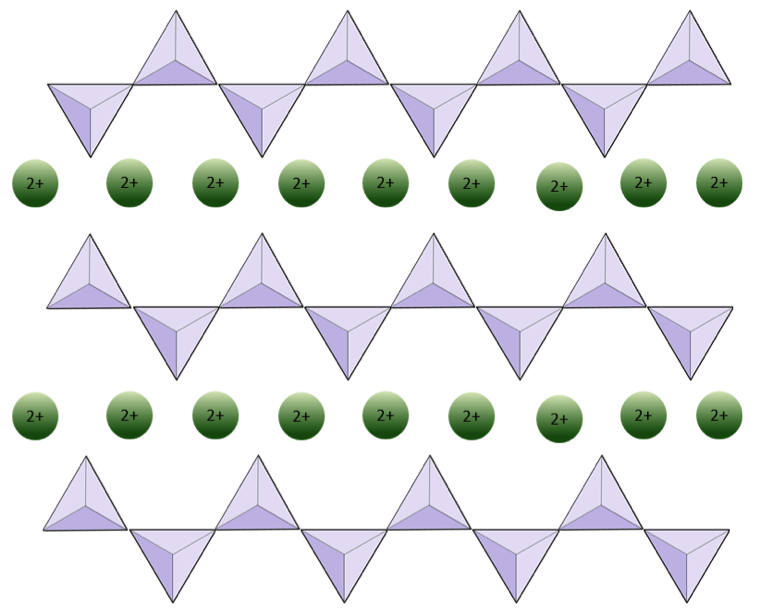
The structure of the single-chain silicate pyroxene is shown on Figures 4.12 and 4.13. In pyroxene, silica tetrahedra are linked together in a single chain, where one oxygen ion from each tetrahedron is shared with the adjacent tetrahedron, hence there are fewer oxygens in the structure. The result is that the oxygen-to-silicon ratio is lower than in olivine (3:1 instead of 4:1), and the net charge per silicon atom is less (–2 instead of –4), since fewer cations are necessary to balance that charge. Pyroxene compositions are of the type MgSiO3, FeSiO3, and CaSiO3, or some combination of these. Pyroxene can also be written as (Mg,Fe,Ca)SiO3, where the elements in the brackets can be present in any proportion. In other words, pyroxene has one cation for each silica tetrahedron (e.g., MgSiO3) while olivine has two (e.g., Mg2SiO4). Because each silicon ion is +4 and each oxygen ion is –2, the three oxygens (–6) and the one silicon (+4) give a net charge of –2 for the single chain of silica tetrahedra. In pyroxene, the one divalent cation (2+) per tetrahedron balances that –2 charge. In olivine, it takes two divalent cations to balance the –4 charge of an isolated tetrahedron.
The structure of pyroxene is more “permissive” than that of olivine — meaning that cations with a wider range of ionic radii can fit into it. That’s why pyroxenes can have iron (radius 0.63 Å) or magnesium (radius 0.72 Å) or calcium (radius 1.00 Å) cations.
Exercises
Exercise 4.4 Oxygen Deprivation
The diagram below represents a single chain in a silicate mineral. Count the number of tetrahedra versus the number of oxygen ions (yellow spheres). Each tetrahedron has one silicon ion so this should give the ratio of Si to O in single-chain silicates (e.g., pyroxene).
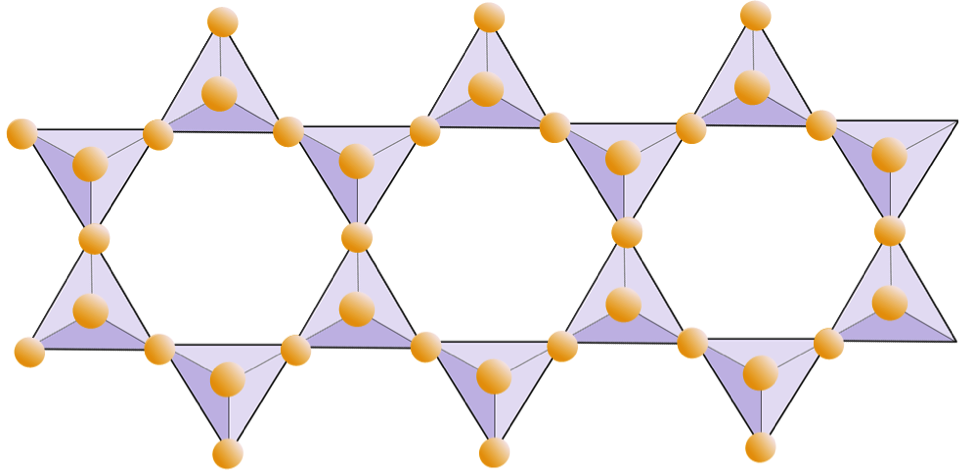
The diagram below represents a double chain in a silicate mineral. Again, count the number of tetrahedra versus the number of oxygen ions. This should give you the ratio of Si to O in double-chain silicates (e.g., amphibole).
In amphibole structures, the silica tetrahedra are linked in a double chain that has an oxygen-to-silicon ratio lower than that of pyroxene, and hence still fewer cations are necessary to balance the charge. Amphibole is even more permissive than pyroxene and its compositions can be very complex. Hornblende, for example, can include sodium, potassium, calcium, magnesium, iron, aluminum, silicon, oxygen, fluorine, and the hydroxyl ion (OH–).
In mica structures, the silica tetrahedra are arranged in continuous sheets, where each tetrahedron shares three oxygen anions with adjacent tetrahedra. There is even more sharing of oxygens between adjacent tetrahedra and hence fewer charge-balancing cations are needed for sheet silicate minerals. Bonding between sheets is relatively weak, and this accounts for the well-developed one-directional cleavage (Figure 2.14). Biotite mica can have iron and/or magnesium in it and that makes it a ferromagnesian silicate mineral (like olivine, pyroxene, and amphibole). Chlorite is another similar mineral that commonly includes magnesium. In muscovite mica, the only cations present are aluminum and potassium; hence it is a non-ferromagnesian silicate mineral.

Apart from muscovite, biotite, and chlorite, there are many other sheet silicates (or phyllosilicates), which usually exist as clay-sized fragments (i.e., less than 0.004 mm). These include the clay minerals kaolinite, illite, and smectite, and although they are difficult to study because of their very small size, they are extremely important components of rocks and especially of soils.
All of the sheet silicate minerals also have water in their structure.
Silica tetrahedra are bonded in three-dimensional frameworks in both the feldspars and quartz. These are non-ferromagnesian minerals — they don’t contain any iron or magnesium. In addition to silica tetrahedra, feldspars include the cations aluminum, potassium, sodium, and calcium in various combinations. Quartz contains only silica tetrahedra.
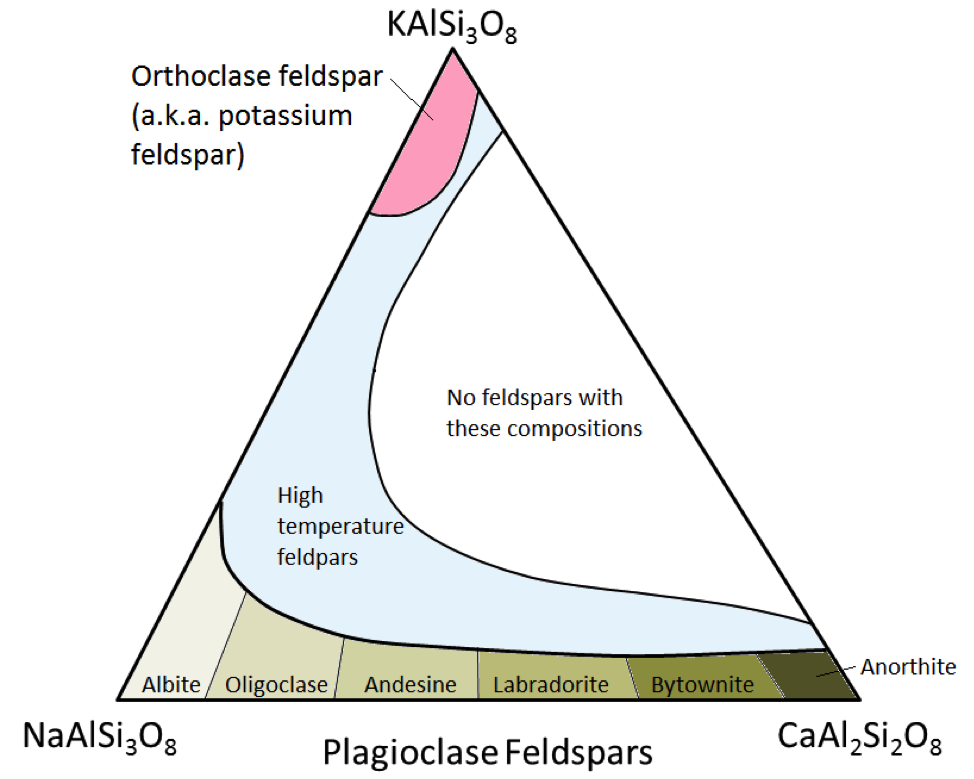
The three main feldspar minerals are potassium feldspar, (a.k.a. K-feldspar or K-spar) and two types of plagioclase feldspar: albite (sodium only) and anorthite (calcium only). As is the case for iron and magnesium in olivine, there is a continuous range of compositions (solid solution series) between albite and anorthite in plagioclase. This is because the calcium and sodium ions are almost identical in size (1.00 Å versus 0.99 Å). Any intermediate compositions between CaAl2Si3O8 and NaAlSi3O8 can exist (Figure 2.15). This is a little bit surprising because, although they are very similar in size, calcium and sodium ions don’t have the same charge (Ca2+ versus Na+). This problem is accounted for by corresponding substitution of Al3+ for Si4+. Therefore, albite is NaAlSi3O8 (one Al and three Si) while anorthite is CaAl2Si2O8 (two Al and two Si), and plagioclase feldspars of intermediate composition have intermediate proportions of Al and Si. This is called a “coupled-substitution.”
The intermediate-composition plagioclase feldspars are oligoclase (10% to 30% Ca), andesine (30% to 50% Ca), labradorite (50% to 70% Ca), and bytownite (70% to 90% Ca). K-feldspar (KAlSi3O8) has a slightly different structure than that of plagioclase, owing to the larger size of the potassium ion (1.37 Å) and because of this large size, potassium and sodium do not readily substitute for each other, except at high temperatures. These high-temperature feldspars are likely to be found only in volcanic rocks because intrusive igneous rocks cool slowly enough to low temperatures for the feldspars to change into one of the lower-temperature forms.
In quartz (SiO2), the silica tetrahedra are bonded in a “perfect” three-dimensional framework. Each tetrahedron is bonded to four other tetrahedra (with an oxygen shared at every corner of each tetrahedron), and as a result, the ratio of silicon to oxygen is 1:2. Since the one silicon cation has a +4 charge and the two oxygen anions each have a –2 charge, the charge is balanced. There is no need for aluminum or any of the other cations such as sodium or potassium. The hardness and lack of cleavage in quartz result from the strong covalent/ionic bonds characteristic of the silica tetrahedron.
Exercises
Exercise 4.5 Ferromagnesian Silicates?
Silicate minerals are classified as being either ferromagnesian or non-ferromagnesian depending on whether or not they have iron (Fe) and/or magnesium (Mg) in their formula. A number of minerals and their formulas are listed below. For each one, indicate whether or not it is a ferromagnesian silicate.
| Mineral | Formula | Ferromagnesian Silicate? |
| olivine | (Mg,Fe)2SiO4 | |
| pyrite | FeS2 | |
| plagioclase | CaAl2Si2O8 | |
| pyroxene | MgSiO3 | |
| hematite | Fe2O3 | |
| orthoclase | KAlSi3O8 | |
| quartz | SiO2 |
| Mineral | Formula* | Ferromagnesian Silicate? |
| amphibole | Fe7Si8O22(OH)2 | |
| muscovite | K2Al4 Si6Al2O20(OH)4 | |
| magnetite | Fe3O4 | |
| biotite | K2Fe4Al2Si6Al4O20(OH)4 | |
| dolomite | (Ca,Mg)CO3 | |
| garnet | Fe2Al2Si3O12 | |
| serpentine | Mg3Si2O5(OH)4 |
*Some of the formulas, especially the more complicated ones, have been simplified.
- An angstrom is the unit commonly used for the expression of atomic-scale dimensions. One angstrom is 10–10 m or 0.0000000001 m. The symbol for an angstrom is Å. ↵