4 Starting with Programming
To err is human. To really foul things up requires a computer.Bill Vaughan – Journalist
Code:
The common term for writing computer programs is coding, as in she is coding the new interface. The program itself is often referred to as the code.
Interactive Programming
Because an interpreted programming language is executed one line at a time, many interpreted programs can be run interactively; that is by entering a single statement on the command line. MatLab is one of those programming languages.
>> 3 + 5ans =8>> 9 - 4ans =5>> 2 .* 5ans =10>> 36 ./ 9ans =4>> 3 .^ 4ans =81>>
Interactive arithmetic
Arithmetic Operations
| Operator | Action | Example |
| + | Addition | |
| – | Subtraction | |
| .* | Multiplication | |
| ./ | Division | |
| . |
Exponentiation |
| Order | Description | Operator |
| 1 | Parentheses | |
| 2 | Exponentiation | |
| 3 | Multiplication | |
| 4 | Division | |
| 5 | Addition | |
| 6 | Subtraction |
The order of operations show that all operations that are enclosed with parentheses take precedence. As an example
(1) 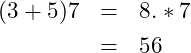
(2) 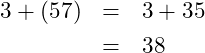
(3) 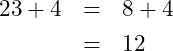
(4) 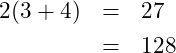
Variables
Variables
>> 7ans =7>>
In fact you could enter a number on the command line, as in figure Storing results in the variable ans, and the system would respond with the same ans =. This is an example of assigning a value to a variable.
Changes to the variable are made using the = called the assignment operator. The action is called an assignment or assigning data to the variable.
>> ans = 5 + 4ans =9>>
>> ans = 9ans =9>> ans = ans ./ 2ans =4.5>>
Updating the variable ans
Creating Variables
>> x = 16x =16>> y = 3.* x - 5y =43>>
There are no limits on the number of variables that you may create in a program, and only a few limitations on what you can name them. The rules are quite simple.
- A variable identifier must begin with a letter of the Latin alphabet
- After the first letter the variable may contain any alpha-numeric character or the underscore symbol, but no other symbols or spaces
- Variables are case sensitive thus a variable with an upper case letter and the same identifier but with lower case letters are two different variables. There are no restrictions on where an upper case or lower case letter may be used
- A variable may not be a keyword. You cannot use names such as function, or end, or while, or any of the additional reserved words
- A variable identifier must begin with a letter of alphabet
- All other characters may be any alpha-numeric character or the underscore symbol
- Variables are case sensitive
- No keywords
>> iskeyword endans =logical1>> iskeyword time2goans =logical0>>
>> isvarname 3xyans =logical0>> isvarname xy3ans =logical1>>
Checking variable identifiers with isvarname
Data Types
If the data is value then MatLab will determine if it is an integer based upon its context. That is if the value contains a fractional part then it will assume that it is a floating point value. If it does not then it will assume that the value is an integer.
>> name = 'Joe Bfstk'name ='Joe Bfstk'>>
Storing a string in a variable
Scripted Programming
The interactive approach to programming works, but lacks efficiency and repeatability. The chances are good that once you write a program you would want to run it multiple times – changing a parameter or two and calculating new results. The would require a program in which all of the executable statements can be run multiple times with little or no changes to the program.
Script:
A script is the program that is written in an interpreted programming language. It consists of a set of commands that will be executed in the sequence in which they are presented.
- parses the line of code
- checks the line for syntax errors
- if an error is found – exits the program
- else
- translates the line to machine code
- executes the statement
- goes to the next line
Writing a script
Story:
-
function driver() -
s = Hello World! -
end
-
>> driver() -
s = Hello World! -
>>
The Hello World Program
This first program was simple but it demonstrates the ideas of a script. The single line of code is parsed – read into memory one character at a time while checking for syntax errors, and then executed.
In this program, a string of text was assigned to a variable and because the line does not end with a semi-colon the value stored in the variable is printed to the screen. Echoing is not the method we want to use for printing but for now it accomplishes the task.
The form of a program
As we begin to write programs – what we will call scripts – it is helpful to develop an efficient approach. Too often programmers will start with a blank screen and starting
writing inputs, then calculations, then outputs. After all, this is the form the program will take when it is done.
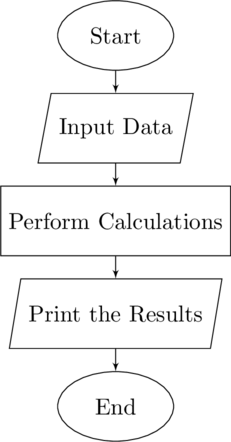
Standard form of a computer program
But it is not how it should be written. While it is the final form of the program, it is inefficient. Instead, a more productive approach is to work in reverse. Create the outputs with all of the formatting to have the results in a form that can be either printed or can be used directly. To do this you will need variables with values. This is what we do first. Do not be concerned with the calculations – they will come later.

Process of efficiently writing a program
Variables in a program can be classified as input variables or output variables. The values in the input variable will later be entered by the user of the program, while the output variables will be the result of calculations. Regardless of the type, at this point they should just be assigned values. This is often called hard coding.
Once the variables in the program have been created and assigned values – both those that will be the inputs and those that will be the outputs to the program – start writing the outputs.
Creating Outputs
A paradox of programming is that we need to be able to print before we learn to enter data, or perform calculations. But why?
While the program we wrote could have performed any task, how would we know it was correct – or even if it ran at all – if we do not have an output? The output is where the user gets to see the result of the program. So while printing the results seems like it should be the last task, it is actually the first.In the Hello World! program you had the script print by calling a function fprintf. There are actually several different ways to print results in your program. Each of them have their own purpose and should be used as such.
Echoing
The first means of printing is called echoing. Echoing is when the results of an operation, be it an input, assignment, or a calculation are printed to the screen immediately after it is done.
Echoing is a type of flag. In programming a flag is a state in the program that indicates that some condition has been met or that some operation should be done. It is called a flag because it only has two possible choices; On or Off – similar to a flag being raised or lowered.
To use echoing you omit the semi-colon from the end of a line. Examples of this are shown in the sample code in the figures earlier.
When the semi-colon is at the end of the line the statement is run exactly like it was before, but nothing is shown on the screen.
Echoing should not be used as the standard print method. Instead it is a debugging tool. When you run your program you can turn echoing on (by removing the ; ) to check if intermediate results are correct.
Warning:
Echoing is a useful technique for checking intermediate results or when using the command line for quick calculations. But it should not be used as the main method for printing results in your programs.
But if you use it throughout you program it becomes a nuisance. Values – in which you are not normally interested – continue to clutter the output. They become a distraction. Instead, once you are assured that the intermediate calculations are correct it is important to turn echoing back off (by ending the line with the ;).
Since echoing should only be used for debugging, standard practice is to end every line of code with the semi-colon; even those that would have printed without the semi-colon.
Display
There is another print function that while it has a use for vectors and matrices is not recommended for normal printing. This is the disp function
disp(variable);
Syntax of the disp function
Unlike echoing in which the variable identifier and the value are printed the disp function will print the variable’s data and nothing else. This function can be used print both text – or strings – as well as numerical data.
-
function driver() -
x = 7 ./ 6; -
disp('Printing using disp'); -
disp(x); -
end
>> driver()Printing using disp1.667>>
Printing using disp
The default for disp is to print the string or value exactly as presented with no other formatting or alignments. It does not print the variable identifier.
The default is to print values using with four digits after the radix point. If the number is small enough it prints it directly while for larger – or smaller values disp prints using scientific notation.
It may occur that you need to know more than four digits in the fractional part. If so you will need to adjust the precision of the output (the number of decimal places).
There are several system commands, in the table, that can set the precision that are printed using disp. Since these are system commands once they called they fix the formatting for echoing and for any other system printing until they are changed or the MatLab session is closed.
| Format Command | |
| Format bank | Two digits after the radix point |
| format compact | Four digits after the radix point |
| format long | Fifteen digits after the radix point |
| format shortEng | Engineering format – scientific notation limited to multiples of three – with four digits after the radix point |
| format longEng | Engineering format – scientific notation limited to multiples of three – with fifteen digits after the radix point |
| format shortG | Either fixed decimal format or scientific notation whichever is shorter each value with four digits after the radix point |
| format longG | Either fixed decimal format or scientific notation whichever is shorter each value with fifteen digits after the radix point |
| format hex | Gexadecimal (base 16) |
| format rat | Ratio of small integers |
| format + | + for positive values, – for negative values, and blank for zero |
| format | Reset to the system default |
Table: Setting precision for the disp function
Warning:
The format command is a system command. This means that it does not apply only to disp or to that run of the program. It applies to both echoing and disp and will remain until it is either changed or the MatLab session ends.
function driver()-
disp('Using default format'); -
x = 53287 ./ 3; -
disp(x); -
format shortEng disp('and now with engineering notation');-
disp(x); -
end
>> driver()Using default format1.7762e+04and now with engineering notation17.7623e+003>>
Changing the precision using the format command
Printing is a primary task in most programs. And while you can print using echoing, it is intended as a debugging tool and should not be used in the final program.
Further disp, while providing a basic means of printing text and data does not include many of the formatting tools that are necessary for controlling how the output is printed.
So while we will continue to use echoing – as a temporary means for printing – disp has been superseded by a printing function that offers more ability to control almost every aspect of printing. This is the function fprintf.
Why is the function fprintf and not just print?
The first f stands for file while the second is for formatted. You use this same function for writing results to files thus the first f. The second part is also important. Formatting means the we control the width of the printed value (the number of spaces that is uses) and also the precision (the number of decimal places).
fprintf
A function in the old C programming language provided a method of printing both strings and data simultaneously. In addition the function enabled a wide range of formatting. This function has been adapted for MatLab as fprintf.
fprintf('formatting string', ouput parameter list);
Syntax of the fprintf function
The formatting string can be as simple as a string of text to be printed. It can – and usually does – include indications as to where to print data. In the sample code, in the figure The Hello World Program, since all that you were going to print is Hello World! the formatting string contained just that. The single quotes at the beginning and end are used to indicate the start and end of the formatting string.
We want more than being able to print strings of text. We want to print our results. This will require formatting.
Formatting the Output
How would you print variables? If you could type them in as text then you just put them inside of the quotes but that is a bit paradoxical. To print them you need to know the values when you write the code. But if you already know the values then there is probably no reason to write a program.
Newline:
There are a pair of characters right before the closing quote. The \n is called an escape sequence. It tells the program to go to a new line at the end of the printing.
You want to be able to print the values after they have been calculated. This is going to require formatting.
We can add several different types of variables to printed. The most common are strings of text, and numerical values.
The location in which you will print text is indicated with a %s while numerical values are positioned using one of several formatting characters. The most common are %f, %d, %e, and %g.
function driver()name = 'Joe Bfstk';month = 'August';day = 23;year = 2025;fprintf('Hello %s!\n', name);fprintf('It is %d %s %d\n', day, month, year);end
- >> driver()
- Hello Joe Bfstk!
- It is 23 August 2025
- >>
Printing your name and date in which name is a string of text and the date consists of two integer values and a string
In the sample code in the figure Printing your name and date in which name is a string of text and the date consists of two integer values and a string the location of the formatting characters indicate where the data will be printed. Which variable is printed is determined by the order that they are presented – first in the list gets printed first, second is second, and so on.
| Format Character | Action |
| %f | Print a floating point value |
| %d | Print an integer value |
| %e | Print a floating point value in scientific notation |
| %g | Print a floating point value in either regular notation or scientific notation whichever is shorter |
| %o | Print an integer in octal (base 8) |
| %x | Print an integer in hexadecimal (base 16) |
| %c | Print a single character |
| %s | Print a string of text |
Table: Formatting Characters
Controlling the width and precision
Precision:
Precision is distance of an observation from the actual value. In the case of coding, precision is determined by the number of decimal places that are retained or printed.
In the standard form the formatting characters provide the location for printing the data value. When they print, whatever is printed abuts the text that comes both immediately before an after it. Additionally, if what is being printed is a a floating point value – a number with a fractional part (or decimal places) – then the default is to print the value with four decimal places.
You may want additional control over the printing. Perhaps you want to align several rows of values o the radix point (the decimal point in base ten). fprintf also provides the ability to control the amount of space – the width – that is reserved for the printed data, and in the case of printing floating point values, the precision.
Each of the formatting characters allow you to set the width that this reserved for printing. This is done by adding a non-negative value between the % and the letter. For example, to print an integer right justified with a minimum of seven spaces reserved you would use %7d. This applies for any of the non-floating point formatting characters.
The syntax for doing this with an integer variable is shown in the figure Syntax for reserving ‘w’ spaces for an integer. Of course the w would be replaced with an integer value.
Radix Point:
The radix point the period that is used to separate the integer part of a floating point number from its fractional part. In base ten it is commonly called the decimal point
fprintf('%wd', integer variable);
Syntax for reserving w spaces for an integer
This same addition will work with all of the non-floating point data types. For example, %32s will reserve 32 spaces for a string of text.
function driver()name = 'Joe Bfstk';month = 'August';day = 23;year = 2025;fprintf('Hello %s!\n', name);fprintf('It is %d %s %d\n', day, month, year);- end
>> driver()Hello Joe Bfstk!It is 23 August 2025>>
Printing your name and date in which name is a string of text and the date consists of two integer values and a string
function driver()fprintf('\n');fprintf('%15s%20s%20s\n', 'Trial', 'Voltage', 'Power');fprintf('\n');end
>> driver()Trial Voltage Power>>
Printing a table header using string variables
function driver()fprintf('\n');fprintf('%15s%20s%20s\n', 'Trial', 'Voltage', 'Power');fprintf('\n');end
>> driver()Trial Voltage Power>>
fprintf('%w.pf', floating_variable);
function driver()% DRIVER driver() is the main or driver function%Assign data to all variablestrial1 = 42;volt1 = 109.74652;power1 = 203.93287;trial2 = 43;volt2 = 73.29876;power2 = 12.30842;%Print the values as a formatted tablefprintf('\n');fprintf('%15s%20s%20s\n', 'Trial', 'Voltage', 'Power');fprintf('%15d%20.2f%20.2f\n', trials, volt, power);fprintf('\n');end
>> driver()Trial Voltage Power42 109.75 203.9343 73.30 12.31>>
Printing strings, decimals, and floating point values
Escape Sequences
| Format | |
| Character | Action |
| \n | Force a new line |
| \r | Carriage return |
| \t | Tab over the print to the next stop |
| \b | Move back a space |
| “ | Print a single quote – ‘ |
| “” | Print a double quote – “ |
| %% | Print the percentage symbol – % |
EscapeSequences
function driver()% DRIVER driver() is the main or driver function%Demonstrate escape sequences for quotes and percentage symbolfprintf('\n');fprintf('Don''t use a single quote or a single %% sign\n');fprintf('\n');end
>> driver()Don't use a single quote or a single % sign>>
Entering the Data into program
Turning data into information requires data, that is any inputs. This can be done in two ways; by hardcoding the values directly into the program, and by having the user enter the data at runtime
Hard coding data
function driver()% DRIVER driver() is the main or driver function%Hard Coded Datadist = 420;fuel = 10.0;eff = dist ./ fuel;fprintf('\n');fprintf('%15s%20.1f miles\n', 'Distance: ', dist);fprintf('%15s%20.4f gallons\n', 'Fuel: ', fuel);fprintf('%15s%20.1f mpg\n', 'Efficiency: ', eff);fprintf('\n');end
>> driver()Distance: 420.0 milesFuel: 10.0000 gallonsEfficiency: 42.0 mpg>>
Input Function
variable = input(prompt);
Syntax of the input function for entering a floating point value
function driver()% DRIVER driver() is the main or driver function% Enter the data for the modeldist = input('Enter distance driven (miles): ');fuel = input('Enter fuel purchased (gallons): ');% Calculate fuel efficiencyeff = dist ./ fuel;% Print the resultsfprintf('\n');fprintf('%15s%20.1f miles\n', 'Distance: ', dist);fprintf('%15s%20.4f gallons\n', 'Fuel: ', fuel);fprintf('%15s%20.1f mpg\n', 'Efficiency: ', eff);fprintf('\n');end
>> driver()Enter distance driven (miles): 380Enter fuel purchased (gallons): 12.3084Distance: 380.0 milesFuel: 12.3084 gallonsEfficiency: 30.9 mpg>>
Entering Numerical Data Using the Input Function
variable = input(prompt, 's');
function driver()% DRIVER driver() is the main or driver function% Enter data as a string of textname = input('Enter your name: ', 's');% Print the resultsfprintf('\n');fprintf('Welcome, %s!\n', name);fprintf('\n');end
>> driver()Enter your name: Joe Bfstk!Welcome, Joe Bfstk>>
Summary
- What is the order of operations in arithmetic?
- What is the result of the following line of code?
-
- What is the result of the following line of code?
-
- What is the result of the following line of code?
-
- What is the result of the following line of code?
-
- What does the command isvarname do?
- What does the command iskeyword do?
- What is echoing?
- How is echoing implemented?
- What does the disp function do?
- How are integers and floating point values different?
- What is precision?
- What is a formatting string?
- What is the formatting string for printing an integer? A floating point value? A string of text?
Projects
- Write a script that uses fprintf with the appropriate formatting to print Hello World! on the screen.
- Write a script in which the user enters two values that are stored in the variables x and y. It then calculates the mean
-
-
- It prints two lines of output. For example, if the user enters
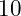 and
and 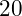 , the program prints
, the program prints
X Y Mean 10.00 20.00 15.00
-
- Write a script in which the user enters two values that are stored in the variables x and y. It then calculates the root-mean-square
-
-
- It prints two lines of output. For example, if the user enters
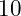 and
and 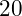 , the program prints the result formatted to two decimal places as
, the program prints the result formatted to two decimal places as
X Y Mean 10.00 20.00 15.81
-
- Write a script in which the user enters the temperature in degrees Fahrenheit and it converts it to degrees Celsius. The transformation formula is
-
-
- The temperatures should be formatted to show two places of precision. A sample output might be
-
- Write a script in which the user enters the temperature in degrees Celsius and it converts it to degrees Fahrenheit. The transformation formula is
-
-
- The temperatures should be formatted to show two places of precision. A sample output might be
-
- A force F acting on a body can be decomposed into its
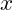 and
and 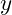 components. This requires the use of the sine and cosine functions;
components. This requires the use of the sine and cosine functions;
-
-
- In MatLab, the functions sind(angle) and cosd(angle) will return the value of the sine and cosine where angle is a variable storing the the angle in degrees the force makes at the point. Write a script in which the user enters two variables; the force F and an angle angle in degrees. It then calculates the decomposition of the force in the
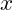 and
and 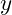 directions. The output should be a table formatted to two decimal places such as
directions. The output should be a table formatted to two decimal places such as
F Angle Fx Fy 100.00 30.00 86.60 50.00
-
- A projectile is launched from the ground at an angle
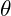 with an initial velocity of
with an initial velocity of 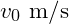 . The time until it hits the ground is
. The time until it hits the ground is
-
-
- where
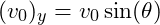 and
and 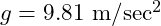 is the acceleration due to gravity.
is the acceleration due to gravity. - Write a script in which the user enters the initial velocity and the initial angle, and the program calculates the time until impact. The output should be a table formatted to two decimal places such as
Velocity (m/sec) Angle (Degrees) Impact (sec) 50.00 60.00 8.83 - Do not use
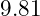 directly in the calculation, but create a variable g and set it to the constant
directly in the calculation, but create a variable g and set it to the constant 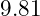 .
.
-
- Three forces are acting at a point at a point. The first is a force of
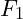 acting at an angle of
acting at an angle of 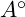 . The second is a force of
. The second is a force of 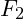 acting at an angle
acting at an angle 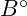 . The third is
. The third is 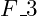 acting at an angle
acting at an angle 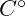 . Write a MatLab program that that analyzes the individual forces and calculates the resultant force. In particular decompose each force into its
. Write a MatLab program that that analyzes the individual forces and calculates the resultant force. In particular decompose each force into its 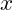 and
and 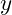 direction components. Then calculate the resulting
direction components. Then calculate the resulting 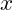 and
and 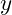 components of the resultant force by summing the component forces. Finally, calculate the overall resultant force and the angle that it would make as a single resultant force. Have the user enter the three forces,
components of the resultant force by summing the component forces. Finally, calculate the overall resultant force and the angle that it would make as a single resultant force. Have the user enter the three forces, 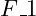 ,
, 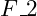 , and
, and 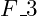 , and the angles that each of these make on the beam,
, and the angles that each of these make on the beam, 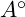 ,
, 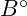 , and
, and 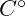 . These are all scalar values. The formulae for decomposing the angles are
. These are all scalar values. The formulae for decomposing the angles are
-
-
- In Matlab, the command to calculate the trig functions for an angle A is sind(A) and cosd(A). The inverse tangent is D = atand(y./x); Your program should print the three forces and their angles with the two component forces for each. You will also print the the two components of the resultant force, the overall resultant force and its angle,
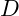 .
.
-

![Rendered by QuickLaTeX.com \[\mbox{rms} = \sqrt{\frac{x^2 + y^2}{2}}\]](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-6a3d19287dca8df9584c5ccebae276b2_l3.png)
![Rendered by QuickLaTeX.com \[t_f = \frac{2(v_0)_y}{g}\]](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-ac7d0e94b71b2d4e93e3fe4832ac750e_l3.png)
![Rendered by QuickLaTeX.com \[F_R = \sqrt{F_{Rx}^2 + F_{Ry}^2} \qquad D = \tan^{-1}\left(\frac{F_{Ry}}{F_{Rx}}\right)\]](https://psu.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-ede9c0e8a29e1495b3b9ceb31e8bef98_l3.png)