Acid-Base Titrations (14.7)
Learning Objectives
By the end of this section, you will be able to:
- Interpret titration curves for strong and weak acid-base systems
- Compute sample pH at important stages of a titration
- Explain the function of acid-base indicators
As seen in the chapter on the stoichiometry of chemical reactions, titrations can be used to quantitatively analyze solutions for their acid or base concentrations. In this section, we will explore the underlying chemical equilibria that make acid-base titrimetry a useful analytical technique.
Titration Curves
A titration curve is a plot of some solution property versus the amount of added titrant. For acid-base titrations, solution pH is a useful property to monitor because it varies predictably with the solution composition and, therefore, may be used to monitor the titration’s progress and detect its end point. The following example exercise demonstrates the computation of pH for a titration solution after additions of several specified titrant volumes. The first example involves a strong acid titration that requires only stoichiometric calculations to derive the solution pH. The second example addresses a weak acid titration requiring equilibrium calculations.
Example 14.21
Calculating pH for Titration Solutions: Strong Acid/Strong Base
A titration is carried out for 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M of a strong base NaOH (the titration curve is shown in Figure 14.18). Calculate the pH at these volumes of added base solution:
(a) 0.00 mL
(b) 12.50 mL
(c) 25.00 mL
(d) 37.50 mL
Solution
(a) Titrant volume = 0 mL. The solution pH is due to the acid ionization of HCl. Because this is a strong acid, the ionization is complete and the hydronium ion molarity is 0.100 M. The pH of the solution is then
pH = − log (0.100) = 1.000
(b) Titrant volume = 12.50 mL. Since the acid sample and the base titrant are both monoprotic and equally concentrated, this titrant addition involves less than a stoichiometric amount of base, and so it is completely consumed by reaction with the excess acid in the sample. The concentration of acid remaining is computed by subtracting the consumed amount from the intial amount and then dividing by the solution volume:
[H3O+] = [latex]\frac{n(H^{+})}{V} = \frac{0.002500 \text{mol} \times ( \frac{1000 \text{mL}}{1 L} ) - 0.100 M \times 12.50 \text{mL}}{25.00 \text{mL} + 12.50 \text{mL}}[/latex] = 0.0333 M
(c) Titrant volume = 25.00 mL. This titrant addition involves a stoichiometric amount of base (the equivalence point), and so only products of the neutralization reaction are in solution (water and NaCl). Neither the cation nor the anion of this salt undergo acid-base ionization; the only process generating hydronium ions is the autoprotolysis of water. The solution is neutral, having a pH = 7.00.
(d) Titrant volume = 37.50 mL. This involves the addition of titrant in excess of the equivalence point. The solution pH is then calculated using the concentration of hydroxide ion:
n(OH−)0 > n(H+)0
[OH-] = [latex]\frac{n(OH^{-})}{V} = \frac{0.100 M \times 35.70 \text{mL} - 0.002500 \text{mol} \times ( \frac{1000 \text{mL}}{1 L} ) }{25.00 \text{mL} + 37.50 \text{mL}}[/latex] = 0.0200 M
pH = 14 - pOH = 14 + log([OH-]) = 14 + log(0.0200) = 12.30
Check Your Learning
Calculate the pH for the strong acid/strong base titration between 50.0 mL of 0.100 M HNO3(aq) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 40.0 mL.
Answer: 0.00: 1.000; 15.0: 1.5111; 25.0: 7; 40.0: 12.523
Example 14.22
Titration of a Weak Acid with a Strong Base
Consider the titration of 25.00 mL of 0.100 M CH3CO2H with 0.100 M NaOH. The reaction can be represented as:
CH3CO2H + OH− ⟶ CH3CO2 − + H2O
Calculate the pH of the titration solution after the addition of the following volumes of NaOH titrant:
(a) 0.00 mL
(b) 25.00 mL
(c) 12.50 mL
(d) 37.50 mL
Solution
(a) The initial pH is computed for the acetic acid solution in the usual ICE approach:
Ka = [latex]\frac{[H_{3}O^{+}][CH_{3}CO_{2}^{-}]}{[CH_{3}CO_{2}H]}[/latex] ≈ [latex]\frac{[H_{3}O^{+}]^{2}}{[CH_{3}CO_{2}H]_{0}}[/latex],
[H3O+] = [latex]sqrt{\text{K}_{a} \times [CH_{3}CO_{2}H]} = \sqrt{1.8 \times 10^{-5} \times 0.100} = 1.3 \times 10^{-3}[/latex]
pH = -log(1.3 x 10-3) = 2.87
(b) The acid and titrant are both monoprotic and the sample and titrant solutions are equally concentrated; thus, this volume of titrant represents the equivalence point. Unlike the strong-acid example above, however, the reaction mixture in this case contains a weak conjugate base (acetate ion). The solution pH is computed considering the base ionization of acetate, which is present at a concentration of
[latex]\frac{0.00250 \text{mol}}{0.0500 L}[/latex] = 0.0500 MCH3CO2-
Base ionization of acetate is represented by the equation
CH3CO2 −(aq) + H2O(l) ⇌ CH3CO2 H(aq) + OH−(aq)
Kb = [latex]\frac{[H^{+}][OH^{-}]}{K_{a}} = \frac{K_{w}}{K_{a}} = \frac{1.0 \times 10^{-14}}{1.8 \times 10^{-5}} = 5.6 \times 10^{-10}[/latex]
Assuming x << 0.0500, the pH may be calculated via the usual ICE approach: Kb = [latex]\frac{x^{2}}{0.0500 M}[/latex]
x = [OH-] = 5.3 x 10-6
pOH = -log(5.3 x 10-6) = 5.28
pH = 14.00 - 5.28 = 8.72
Note that the pH at the equivalence point of this titration is significantly greater than 7, as expected when titrating a weak acid with a strong base.
(c) Titrant volume = 12.50 mL. This volume represents one-half of the stoichiometric amount of titrant, and so one-half of the acetic acid has been neutralized to yield an equivalent amount of acetate ion. The concentrations of these conjugate acid-base partners, therefore, are equal. A convenient approach to computing the pH is use of the Henderson-Hasselbalch equation:
pH = pKa + log[latex]\frac{[Base]}{[Acid]}[/latex] = -log(Ka) + log[latex]\frac{[CH_{3}CO_{2}^{-}]}{[CH_{3}CO_{2}H]}[/latex] = -log(1.8 x 10-5) + log(1)
pH = -log(1.8 x 10-5) = 4.74
(pH = pKa at the half-equivalence point in a titration of a weak acid)
(d) Titrant volume = 37.50 mL. This volume represents a stoichiometric excess of titrant, and a reaction solution containing both the titration product, acetate ion, and the excess strong titrant. In such solutions, the solution pH is determined primarily by the amount of excess strong base:
[OH-] = [latex]\frac{(0.003750 \text{mol} - 0.00250 \text{mol})}{0.06250 \text{L}}[/latex] = 2.00 x 10-2 M
pOH = -log(2.00 x 10-2) = 1.70, and pH = 14.00 - 1.70 = 12.30
Check Your Learning
Calculate the pH for the weak acid/strong base titration between 50.0 mL of 0.100 M HCOOH(aq) (formic acid) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 30.0 mL.
Answer: 0.00 mL: 2.37; 15.0 mL: 3.92; 25.00 mL: 8.29; 30.0 mL: 12.097
Performing additional calculations similar to those in the preceding example permits a more full assessment of titration curves. A summary of pH/volume data pairs for the strong and weak acid titrations is provided in Table 14.2 and plotted as titration curves in Figure 14.18. A comparison of these two curves illustrates several important concepts that are best addressed by identifying the four stages of a titration:
- initial state (added titrant volume = 0 mL): pH is determined by the acid being titrated; because the two acid samples are equally concentrated, the weak acid will exhibit a greater initial pH
- pre-equivalence point (0 mL < V < 25 mL): solution pH increases gradually and the acid is consumed by reaction with added titrant; composition includes unreacted acid and the reaction product, its conjugate base
- equivalence point (V = 25 mL): a drastic rise in pH is observed as the solution composition transitions from acidic to either neutral (for the strong acid sample) or basic (for the weak acid sample), with pH determined by ionization of the conjugate base of the acid
- postequivalence point (V > 25 mL): pH is determined by the amount of excess strong base titrant added; since both samples are titrated with the same titrant, both titration curves appear similar at this stage.
pH Values in the Titrations of a Strong Acid and of a Weak Acid
|
Volume of 0.100 M NaOH Added (mL) |
Moles of NaOH Added |
pH Values 0.100 M HCl[1] |
pH Values 0.100 M CH3CO2H[2] |
|
0.0 |
0.0 |
1.00 |
2.87 |
|
5.0 |
0.00050 |
1.18 |
4.14 |
|
10.0 |
0.00100 |
1.37 |
4.57 |
|
15.0 |
0.00150 |
1.60 |
4.92 |
|
20.0 |
0.00200 |
1.95 |
5.35 |
|
22.0 |
0.00220 |
2.20 |
5.61 |
|
24.0 |
0.00240 |
2.69 |
6.13 |
|
24.5 |
0.00245 |
3.00 |
6.44 |
|
24.9 |
0.00249 |
3.70 |
7.14 |
|
25.0 |
0.00250 |
7.00 |
8.72 |
|
25.1 |
0.00251 |
10.30 |
10.30 |
|
25.5 |
0.00255 |
11.00 |
11.00 |
|
26.0 |
0.00260 |
11.29 |
11.29 |
|
28.0 |
0.00280 |
11.75 |
11.75 |
|
30.0 |
0.00300 |
11.96 |
11.96 |
|
35.0 |
0.00350 |
12.22 |
12.22 |
|
40.0 |
0.00400 |
12.36 |
12.36 |
|
45.0 |
0.00450 |
12.46 |
12.46 |
|
50.0 |
0.00500 |
12.52 |
12.52 |
Table 14.2
1. Titration of 25.00 mL of 0.100 M HCl (0.00250 mol of HCI) with 0.100 M NaOH.
2. Titration of 25.00 mL of 0.100 M CH3CO2H (0.00250 mol of CH3CO2H) with 0.100 M NaOH.
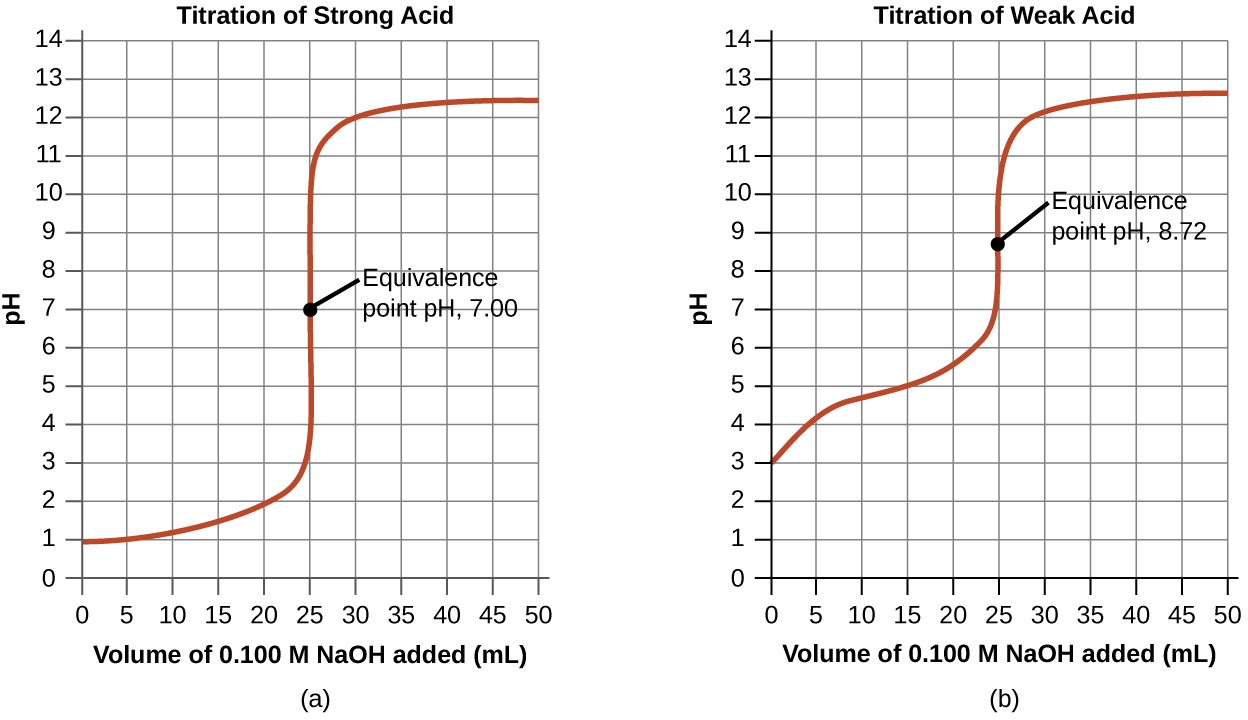
Figure 14.18 (a) The titration curve for the titration of 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M NaOH (strong base) has an equivalence point of 7.00 pH. (b) The titration curve for the titration of 25.00 mL of 0.100 M acetic acid (weak acid) with 0.100 M NaOH (strong base) has an equivalence point of 8.72 pH.
Acid-Base Indicators
Certain organic substances change color in dilute solution when the hydronium ion concentration reaches a particular value. For example, phenolphthalein is a colorless substance in any aqueous solution with a hydronium ion concentration greater than 5.0 × 10−9 M (pH < 8.3). In more basic solutions where the hydronium ion concentration is less than 5.0 × 10−9 M (pH > 8.3), it is red or pink. Substances such as phenolphthalein, which can be used to determine the pH of a solution, are called acid-base indicators. Acid-base indicators are either weak organic acids or weak organic bases.
The equilibrium in a solution of the acid-base indicator methyl orange, a weak acid, can be represented by an equation in which we use HIn as a simple representation for the complex methyl orange molecule:
HIn(aq) + H2O(l) ⇌ H3O+(aq) + In−(aq)
Red Yellow
Ka = [latex]\frac{[H_{3}O^{+}][In^{-}]}{[HIn]}[/latex] = 4.0 x 10-4
The anion of methyl orange, In−, is yellow, and the nonionized form, HIn, is red. When we add acid to a solution of methyl orange, the increased hydronium ion concentration shifts the equilibrium toward the nonionized red form, in accordance with Le Châtelier’s principle. If we add base, we shift the equilibrium towards the yellow form. This behavior is completely analogous to the action of buffers.
The perceived color of an indicator solution is determined by the ratio of the concentrations of the two species In− and HIn. If most of the indicator (typically about 60−90% or more) is present as In−, the perceived color of the solution is yellow. If most is present as HIn, then the solution color appears red. The Henderson-Hasselbalch equation is useful for understanding the relationship between the pH of an indicator solution and its composition (thus, perceived color):
pH = pKa + log[latex]( \frac{[In^{-}]}{[HIn]} )[/latex]
In solutions where pH > pKa, the logarithmic term must be positive, indicating an excess of the conjugate base form of the indicator (yellow solution). When pH > pKa, the log term must be negative, indicating an excess of the conjugate acid (red solution). When the solution pH is close to the indicator pKa, appreciable amounts of both conjugate partners are present, and the solution color is that of an additive combination of each (yellow and red, yielding orange). The color change interval (or pH interval) for an acid-base indicator is defined as the range of pH values over which a change in color is observed, and for most indicators this range is approximately p Ka ± 1.
There are many different acid-base indicators that cover a wide range of pH values and can be used to determine the approximate pH of an unknown solution by a process of elimination. Universal indicators and pH paper contain a mixture of indicators and exhibit different colors at different pHs. Figure 14.19 presents several indicators, their colors, and their color-change intervals.
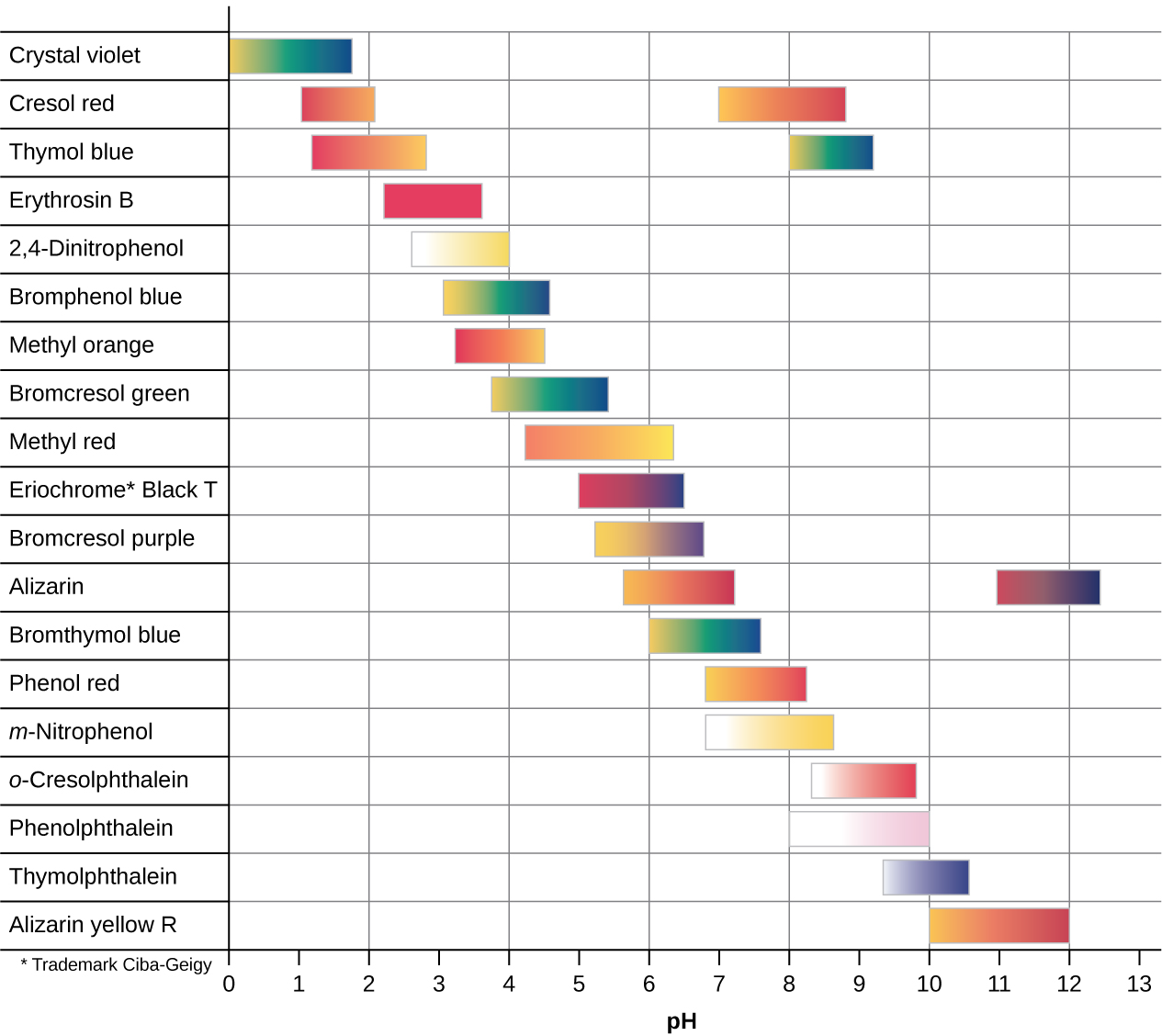
Figure 14.19 This chart illustrates the color change intervals for several acid-base indicators.
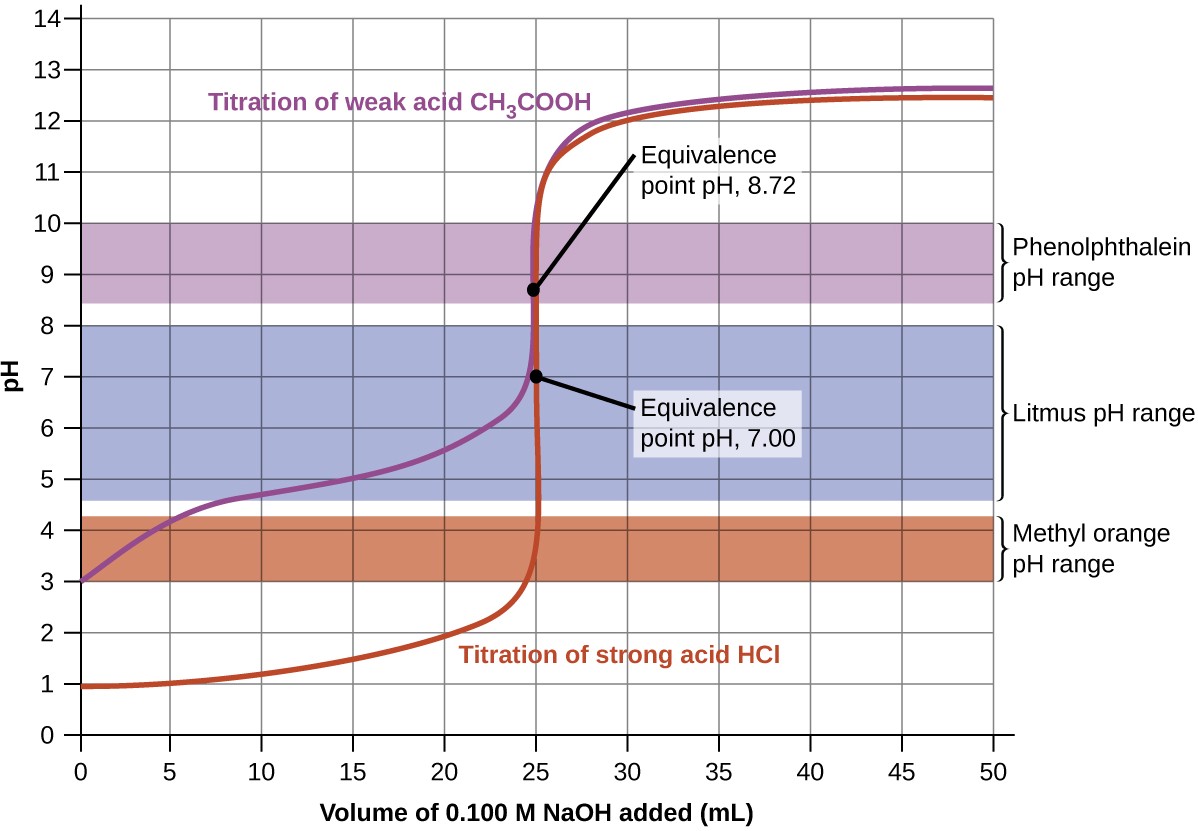
Figure 14.20 Titration curves for strong and weak acids illustrating the proper choice of acid-base indicator. Any of the three indicators will exhibit a reasonably sharp color change at the equivalence point of the strong acid titration, but only phenolphthalein is suitable for use in the weak acid titration.
The titration curves shown in Figure 14.20 illustrate the choice of a suitable indicator for specific titrations. In the strong acid titration, use of any of the three indicators should yield reasonably sharp color changes and accurate end point determinations. For this titration, the solution pH reaches the lower limit of the methyl orange color change interval after addition of ~24 mL of titrant, at which point the initially red solution would begin to appear orange. When 25 mL of titrant has been added (the equivalence point), the pH is well above the upper limit and the solution will appear yellow. The titration's end point may then be estimated as the volume of titrant that yields a distinct orange-to-yellow color change. This color change would be challenging for most human eyes to precisely discern. More-accurate estimates of the titration end point are possible using either litmus or phenolphthalein, both of which exhibit color change intervals that are encompassed by the steep rise in pH that occurs around the 25.00 mL equivalence point.
The weak acid titration curve in Figure 14.20 shows that only one of the three indicators is suitable for end point detection. If methyl orange is used in this titration, the solution will undergo a gradual red-to-orange-to-yellow color change over a relatively large volume interval (0–6 mL), completing the color change well before the equivalence point (25 mL) has been reached. Use of litmus would show a color change that begins after adding 7 – 8 mL of titrant and ends just before the equivalence point. Phenolphthalein, on the other hand, exhibits a color change interval that nicely brackets the abrupt change in pH occurring at the titration's equivalence point. A sharp color change from colorless to pink will be observed within a very small volume interval around the equivalence point.
Key Terms
acid ionization reaction involving the transfer of a proton from an acid to water, yielding hydronium ions and the conjugate base of the acid
acid ionization constant (Ka) equilibrium constant for an acid ionization reaction
acid-base indicator weak acid or base whose conjugate partner imparts a different solution color; used in visual assessments of solution pH
acidic a solution in which [H3O+] > [OH−]
amphiprotic species that may either donate or accept a proton in a Bronsted-Lowry acid-base reaction
amphoteric species that can act as either an acid or a base
autoionization reaction between identical species yielding ionic products; for water, this reaction involves transfer of protons to yield hydronium and hydroxide ions
base ionization reaction involving the transfer of a proton from water to a base, yielding hydroxide ions and the conjugate acid of the base
base ionization constant (Kb) equilibrium constant for a base ionization reaction
basic a solution in which [H3O+] < [OH−]
Brønsted-Lowry acid Proton donor
Brønsted-Lowry base Proton acceptor
buffer mixture of appreciable amounts of a weak acid-base pair the pH of a buffer resists change when small amounts of acid or base are added
buffer capacity amount of an acid or base that can be added to a volume of a buffer solution before its pH changes significantly (usually by one pH unit)
color-change interval range in pH over which the color change of an indicator is observed
conjugate acid substance formed when a base gains a proton
conjugate base substance formed when an acid loses a proton
diprotic acid acid containing two ionizable hydrogen atoms per molecule
diprotic base base capable of accepting two protons
Henderson-Hasselbalch equation logarithmic version of the acid ionization constant expression, conveniently formatted for calculating the pH of buffer solutions
ion-product constant for water (Kw) equilibrium constant for the autoionization of water
leveling effect observation that acid-base strength of solutes in a given solvent is limited to that of the solvent’s characteristic acid and base species (in water, hydronium and hydroxide ions, respectively)
monoprotic acid acid containing one ionizable hydrogen atom per molecule
neutral describes a solution in which [H3O+] = [OH−]
oxyacid ternary compound with acidic properties, molecules of which contain a central nonmetallic atom bonded to one or more O atoms, at least one of which is bonded to an ionizable H atom
percent ionization ratio of the concentration of ionized acid to initial acid concentration expressed as a percentage
pH logarithmic measure of the concentration of hydronium ions in a solution
pOH logarithmic measure of the concentration of hydroxide ions in a solution
stepwise ionization process in which a polyprotic acid is ionized by losing protons sequentially
titration curve plot of some sample property (such as pH) versus volume of added titrant
triprotic acid acid that contains three ionizable hydrogen atoms per molecule
Key Equations
- Kw = [H3O+][OH−] = 1.0 × 10−14 (at 25 °C)
- pH = −log[H3O+]
- pOH = −log[OH−]
- [H3O+] = 10−pH
- [OH−] = 10−pOH
- pH + pOH = pKw = 14.00 at 25 °C
- Ka = [latex]\frac{[H_{3}O^{+}][A^{-}]}{[HA]}[/latex]
- Kb = [latex]\frac{[HB^{+}][OH^{-}]}{[B]}[/latex]
- Ka × Kb = 1.0 × 10−14 = Kw
- Percent ionization = [latex]\frac{[H_{3}O^{+}]\text{eq}}{[HA]_{0}}[/latex] x 100
- pKa = −log Ka
- pKb = −log Kb
- pH = pKa + log $latex \frac{[A^{-}]}{[HA]}
Summary
Brønsted-Lowry Acids and Bases
A compound that can donate a proton (a hydrogen ion) to another compound is called a Brønsted-Lowry acid. The compound that accepts the proton is called a Brønsted-Lowry base. The species remaining after a Brønsted-Lowry acid has lost a proton is the conjugate base of the acid. The species formed when a Brønsted-Lowry base gains a proton is the conjugate acid of the base. Thus, an acid-base reaction occurs when a proton is transferred from an acid to a base, with formation of the conjugate base of the reactant acid and formation of the conjugate acid of the reactant base. Amphiprotic species can act as both proton donors and proton acceptors. Water is the most important amphiprotic species. It can form both the hydronium ion, H3O+, and the hydroxide ion, OH− when it undergoes autoionization:
2H2O(l) ⇌ H3O+(aq) + OH−(aq)
The ion product of water, Kw is the equilibrium constant for the autoionization reaction:
Kw = [H3O+][OH−] = 1.0 × 10−14 at 25 °C
Concentrations of hydronium and hydroxide ions in aqueous media are often represented as logarithmic pH and pOH values, respectively. At 25 °C, the autoprotolysis equilibrium for water requires the sum of pH and pOH to equal 14 for any aqueous solution. The relative concentrations of hydronium and hydroxide ion in a solution define its status as acidic ([H3O+] > [OH−]), basic ([H3O+] < [OH−]), or neutral ([H3O+] = [OH−]). At 25 °C, a pH < 7 indicates an acidic solution, a pH > 7 a basic solution, and a pH = 7 a neutral solution.
Relative Strengths of Acids and Bases
The relative strengths of acids and bases are reflected in the magnitudes of their ionization constants; the stronger the acid or base, the larger its ionization constant. A reciprocal relation exists between the strengths of a conjugate acid-base pair: the stronger the acid, the weaker its conjugate base. Water exerts a leveling effect on dissolved acids or bases, reacting completely to generate its characteristic hydronium and hydroxide ions (the strongest acid and base that may exist in water). The strengths of the binary acids increase from left to right across a period of the periodic table (CH4 < NH3 < H2O < HF), and they increase down a group (HF < HCl < HBr < HI). The strengths of oxyacids that contain the same central element increase as the oxidation number of the element increases (H2SO3 < H2SO4). The strengths of oxyacids also increase as the electronegativity of the central element increases [H 2SeO4 < H2SO4].
Hydrolysis of Salts
The ions composing salts may possess acidic or basic character, ionizing when dissolved in water to yield acidic or basic solutions. Acidic cations are typically the conjugate partners of weak bases, and basic anions are the conjugate partners of weak acids. Many metal ions bond to water molecules when dissolved to yield complex ions that may function as acids.
Polyprotic Acids
An acid that contains more than one ionizable proton is a polyprotic acid. These acids undergo stepwise ionization reactions involving the transfer of single protons. The ionization constants for polyprotic acids decrease with each subsequent step; these decreases typically are large enough to permit simple equilibrium calculations that treat each step separately.
Buffers
Solutions that contain appreciable amounts of a weak conjugate acid-base pair are called buffers. A buffered solution will experience only slight changes in pH when small amounts of acid or base are added. Addition of large amounts of acid or base can exceed the buffer capacity, consuming most of one conjugate partner and preventing further buffering action.
Acid-Base Titrations
The titration curve for an acid-base titration is typically a plot of pH versus volume of added titrant. These curves are useful in selecting appropriate acid-base indicators that will permit accurate determinations of titration end points.
Exercises
Brønsted-Lowry Acids and Bases
- Write equations that show NH3 as both a conjugate acid and a conjugate base.
- Write equations that show H2 PO4 − acting both as an acid and as a base.
- Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry acid:
- H3O+
- HCl
- NH3
- CH3CO2H
- NH4 +
- HSO4 −
- Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry acid:
- HNO3
- PH4 +
- H2S
- CH3CH2COOH
- H2PO4 −
- HS−
- Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry base:
- H2O
- OH−
- NH3
- CN−
- S2−
- H2PO4 −
- Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry base:
- HS−
- PO4 3−
- NH2 −
- C2H5OH
- O2−
- H2PO4 −
- What is the conjugate acid of each of the following? What is the conjugate base of each?
- OH−
- H2O
- HCO3 −
- NH3
- HSO4 −
- H2O2
- HS−
- H5 N2 +
- What is the conjugate acid of each of the following? What is the conjugate base of each?
- H2S
- H2PO4 −
- PH3
- HS−
- HSO3 −
- H3 O2 +
- H4N2
- CH3OH
- Identify and label the Brønsted-Lowry acid, its conjugate base, the Brønsted-Lowry base, and its conjugate acid in each of the following equations:
- HNO3 + H2O ⟶ H3O+ + NO3 −
- CN− + H2O ⟶ HCN + OH−
- H2SO4 + Cl− ⟶ HCl + HSO4 −
- HSO4 − + OH− ⟶ SO4 2− + H2O
- O2− + H2O ⟶ 2OH−
- [Cu(H2O)3(OH)]+ + [Al(H2O)6]3+ ⟶ [Cu(H2O)4]2+ + [Al(H2O)5(OH)]2+
- H2S + NH2 − ⟶ HS− + NH3
- Identify and label the Brønsted-Lowry acid, its conjugate base, the Brønsted-Lowry base, and its conjugate acid in each of the following equations:
- NO2 − + H2O ⟶ HNO2 + OH−
- HBr + H2O ⟶ H3O+ + Br−
- HS− + H2O ⟶ H2S + OH−
- H2PO4 − + OH− ⟶ HPO4 2− + H2 O
- H2PO4 − + HCl ⟶ H3PO4 + Cl−
- [Fe(H2O)5(OH)]2+ + [Al(H2O)6]3+ ⟶ [Fe(H2O)6]3+ + [Al(H2O)5(OH)]2+
- CH3OH + H− ⟶ CH3O− + H2
- What are amphiprotic species? Illustrate with suitable equations.
- State which of the following species are amphiprotic and write chemical equations illustrating the amphiprotic character of these species:
- H2O
- H2PO4 −
- S2−
- CO3 2−
- HSO4 −
- State which of the following species are amphiprotic and write chemical equations illustrating the amphiprotic character of these species.
- NH3
- HPO4 −
- Br−
- NH4 +
- ASO4 3−
- Is the self-ionization of water endothermic or exothermic? The ionization constant for water ( Kw) is 2.9 × 10−14 at 40 °C and 9.3 × 10−14 at 60 °C.
- Explain why a sample of pure water at 40 °C is neutral even though [H3O+] = 1.7 × 10−7 M. Kw is 2.9 × 10−14 at 40 °C.
- The ionization constant for water (Kw) is 2.9 × 10−14 at 40 °C. Calculate [H3O+], [OH−], pH, and pOH for pure water at 40 °C.
- The ionization constant for water (Kw) is 9.311 × 10−14 at 60 °C. Calculate [H3O+], [OH−], pH, and pOH for pure water at 60 °C.
- Calculate the pH and the pOH of each of the following solutions at 25 °C for which the substances ionize completely:
- 0.200 M HCl
- 0.0143 M NaOH
- 3.0 M HNO3
- 0.0031 M Ca(OH)2
- Calculate the pH and the pOH of each of the following solutions at 25 °C for which the substances ionize completely:
- 0.000259 M HClO4
- 0.21 M NaOH
- 0.000071 M Ba(OH)2
- 2.5 M KOH
- What are the pH and pOH of a solution of 2.0 M HCl, which ionizes completely?
- What are the hydronium and hydroxide ion concentrations in a solution whose pH is 6.52?
- Calculate the hydrogen ion concentration and the hydroxide ion concentration in wine from its pH. See Figure 14.2 for useful information.
- Calculate the hydronium ion concentration and the hydroxide ion concentration in lime juice from its pH. See Figure 14.2 for useful information.
- The hydronium ion concentration in a sample of rainwater is found to be 1.7 × 10−6 M at 25 °C. What is the concentration of hydroxide ions in the rainwater?
- The hydroxide ion concentration in household ammonia is 3.2 × 10−3 M at 25 °C. What is the concentration of hydronium ions in the solution?
- Explain why the neutralization reaction of a strong acid and a weak base gives a weakly acidic solution.
- Explain why the neutralization reaction of a weak acid and a strong base gives a weakly basic solution.
- Use this list of important industrial compounds (and Figure 14.8) to answer the following questions regarding: CaO, Ca(OH)2, CH3CO2H, CO2, HCl, H2CO3, HF, HNO2, HNO3, H3PO4, H2SO4, NH3, NaOH, Na2CO3.
- Identify the strong Brønsted-Lowry acids and strong Brønsted-Lowry bases.
- List those compounds in (a) that can behave as Brønsted-Lowry acids with strengths lying between those of H3O+ and H2O.
- List those compounds in (a) that can behave as Brønsted-Lowry bases with strengths lying between those of H 2O and OH−.
- The odor of vinegar is due to the presence of acetic acid, CH3CO2H, a weak acid. List, in order of descending concentration, all of the ionic and molecular species present in a 1-M aqueous solution of this acid.
- Household ammonia is a solution of the weak base NH3 in water. List, in order of descending concentration, all of the ionic and molecular species present in a 1-M aqueous solution of this base.
- Explain why the ionization constant, Ka, for H2SO4 is larger than the ionization constant for H2SO3.
- Explain why the ionization constant, Ka, for HI is larger than the ionization constant for HF.
- Gastric juice, the digestive fluid produced in the stomach, contains hydrochloric acid, HCl. Milk of Magnesia, a suspension of solid Mg(OH)2 in an aqueous medium, is sometimes used to neutralize excess stomach acid. Write a complete balanced equation for the neutralization reaction, and identify the conjugate acid-base pairs.
- Nitric acid reacts with insoluble copper(II) oxide to form soluble copper(II) nitrate, Cu(NO3)2, a compound that has been used to prevent the growth of algae in swimming pools. Write the balanced chemical equation for the reaction of an aqueous solution of HNO3 with CuO.
- What is the ionization constant at 25 °C for the weak acid CH3 NH3 +, the conjugate acid of the weak base CH3NH2, Kb = 4.4 × 10−4.
- What is the ionization constant at 25 °C for the weak acid (CH3)2 NH2 +, the conjugate acid of the weak base (CH3)2NH, Kb = 5.9 × 10−4?
- Which base, CH3NH2 or (CH3)2NH, is the stronger base? Which conjugate acid, (CH3)2 NH2 + or CH3 NH3 + , is the stronger acid?
- Which is the stronger acid, NH4 + or HBrO?
- Which is the stronger base, (CH3)3N or H2 BO3 − ?
- Predict which acid in each of the following pairs is the stronger and explain your reasoning for each.
- H2O or HF
- B(OH)3 or Al(OH)3
- HSO3 − or HSO4 −
- NH3 or H2S
- H2O or H2Te
- Predict which compound in each of the following pairs of compounds is more acidic and explain your reasoning for each.
- HSO4 − or HSeO4 −
- NH3 or H2O
- PH3 or HI
- NH3 or PH3
- H2S or HBr
- Rank the compounds in each of the following groups in order of increasing acidity or basicity, as indicated, and explain the order you assign.
- acidity: HCl, HBr, HI
- basicity: H2O, OH−, H−, Cl−
- basicity: Mg(OH)2, Si(OH)4, ClO3(OH) (Hint: Formula could also be written as HClO4.)
- acidity: HF, H2O, NH3, CH4
- Rank the compounds in each of the following groups in order of increasing acidity or basicity, as indicated, and explain the order you assign.
- acidity: NaHSO3, NaHSeO3, NaHSO4
- basicity: BrO2 −, ClO2 −, IO2 −
- acidity: HOCl, HOBr, HOI
- acidity: HOCl, HOClO, HOClO2, HOClO3
- basicity: NH2 −, HS−, HTe−, PH2 −
- basicity: BrO−, BrO2 −, BrO3 −, BrO4 −
- Both HF and HCN ionize in water to a limited extent. Which of the conjugate bases, F− or CN−, is the stronger base?
- The active ingredient formed by aspirin in the body is salicylic acid, C6H4OH(CO2H). The carboxyl group (−CO2H) acts as a weak acid. The phenol group (an OH group bonded to an aromatic ring) also acts as an acid but a much weaker acid. List, in order of descending concentration, all of the ionic and molecular species present in a 0.001-M aqueous solution of C6H4OH(CO2H).
- Are the concentrations of hydronium ion and hydroxide ion in a solution of an acid or a base in water directly proportional or inversely proportional? Explain your answer.
- What two common assumptions can simplify calculation of equilibrium concentrations in a solution of a weak acid or base?
- Which of the following will increase the percent of NH3 that is converted to the ammonium ion in water?
- addition of NaOH
- addition of HCl
- addition of NH4Cl
- Which of the following will increase the percentage of HF that is converted to the fluoride ion in water?
- addition of NaOH
- addition of HCl
- addition of NaF
- What is the effect on the concentrations of NO2 −, HNO2, and OH− when the following are added to a solution of KNO2 in water:
- HCl
- HNO2
- NaOH
- NaCl
- KNO
- What is the effect on the concentration of hydrofluoric acid, hydronium ion, and fluoride ion when the following are added to separate solutions of hydrofluoric acid?
- HCl
- KF
- NaCl
- KOH
- HF
- Why is the hydronium ion concentration in a solution that is 0.10 M in HCl and 0.10 M in HCOOH determined by the concentration of HCl?
- From the equilibrium concentrations given, calculate Ka for each of the weak acids and Kb for each of the weak bases.
- CH3CO2H: [H3 O+] = 1.34 × 10−3 M;
[CH3 CO2 −] = 1.34 × 10−3 M;
[CH3CO2H] = 9.866 × 10−2 M - ClO−: [OH−] = 4.0 × 10−4M;
[HClO] = 2.38 × 10−4 M;
[ClO−] = 0.273 M; - HCO2H: [HCO2H] = 0.524 M;
[H3 O+] = 9.8 × 10−3 M;
[HCO2 −] = 9.8 × 10−3 M; - C6 H5 NH3 + : [C6 H5 NH3 +] = 0.233 M;
[C6H5NH2] = 2.3 × 10−3 M;[H3 O+] = 2.3 × 10−3 M
- CH3CO2H: [H3 O+] = 1.34 × 10−3 M;
- From the equilibrium concentrations given, calculate Ka for each of the weak acids and Kb for each of the weak bases.
- NH3: [OH−] = 3.1 × 10−3 M;
[NH4 +] = 3.1 × 10−3 M;
[NH3] = 0.533 M; - HNO2: [H3O+] = 0.011 M;
[NO2 −] = 0.0438 M;
[HNO2] = 1.07 M; - (CH3)3N: [(CH3)3N] = 0.25 M;
[(CH3)3NH+] = 4.3 × 10−3 M;
[OH−] = 3.7 × 10−3 M; - NH4 + : [NH4 +] = 0.100 M;
[NH3] = 7.5 × 10−6 M;
[H3O+] = 7.5 × 10−6 M
- NH3: [OH−] = 3.1 × 10−3 M;
- Determine Kb for the nitrite ion, NO2 −. In a 0.10-M solution this base is 0.0015% ionized.
- Determine Ka for hydrogen sulfate ion, HSO4 −. In a 0.10-M solution the acid is 29% ionized.
- Calculate the ionization constant for each of the following acids or bases from the ionization constant of its conjugate base or conjugate acid:
- F−
- NH4 +
- AsO4 3−
- (CH3)2 NH2 +
- NO2 −
- HC2O4 − (as a base)
- Calculate the ionization constant for each of the following acids or bases from the ionization constant of its conjugate base or conjugate acid:
- HTe− (as a base)
- (CH3)3 NH+
- HAsO4 3− (as a base)
- HO2 − (as a base)
- C6H5 NH3 +
- HSO3 − (as a base)
- Using the Ka value of 1.4 × 10−5, place Al(H2 O)6 3+ in the correct location in Figure14.7.
- Calculate the concentration of all solute species in each of the following solutions of acids or bases. Assume that the ionization of water can be neglected, and show that the change in the initial concentrations can be neglected.
- 0.0092 M HClO, a weak acid
- 0.0784 M C6H5NH2, a weak base
- 0.0810 M HCN, a weak acid
- 0.11 M (CH3)3N, a weak base
- 0.120 M Fe(H2O)6 2+ a weak acid, Ka = 1.6 × 10−7
- Propionic acid, C2H5CO2H (Ka = 1.34 × 10−5), is used in the manufacture of calcium propionate, a food preservative. What is the pH of a 0.698-M solution of C2H5CO2H?
- White vinegar is a 5.0% by mass solution of acetic acid in water. If the density of white vinegar is 1.007 g/cm3, what is the pH?
- The ionization constant of lactic acid, CH3CH(OH)CO2H, an acid found in the blood after strenuous exercise, is 1.36 × 10−4. If 20.0 g of lactic acid is used to make a solution with a volume of 1.00 L, what is the concentration of hydronium ion in the solution?
- Nicotine, C10H14N2, is a base that will accept two protons (Kb1 = 7 × 10−7, Kb2 = 1.4 × 10−11). What is the concentration of each species present in a 0.050-M solution of nicotine?
- The pH of a 0.23-M solution of HF is 1.92. Determine Ka for HF from these data.
- The pH of a 0.15-M solution of HSO4 − is 1.43. Determine Ka for HSO4 − from these data.
- The pH of a 0.10-M solution of caffeine is 11.70. Determine Kb for caffeine from these data: C8H10N4O2(aq) + H2O(l) ⇌ C8H10N4O2H+(aq) + OH−(aq)
- The pH of a solution of household ammonia, a 0.950 M solution of NH3, is 11.612. Determine Kb for NH3 from these data.
- Determine whether aqueous solutions of the following salts are acidic, basic, or neutral:
- Al(NO3)3
- RbI
- KHCO2
- CH3NH3Br
- Determine whether aqueous solutions of the following salts are acidic, basic, or neutral:
- FeCl3
- K2CO3
- NH4Br
- KClO4
- Novocaine, C13H21O2N2Cl, is the salt of the base procaine and hydrochloric acid. The ionization constant for procaine is 7 × 10−6. Is a solution of novocaine acidic or basic? What are [H3O+], [OH−], and pH of a 2.0% solution by mass of novocaine, assuming that the density of the solution is 1.0 g/mL.
- Which of the following concentrations would be practically equal in a calculation of the equilibrium concentrations in a 0.134-M solution of H2CO3, a diprotic acid: [H3O+], [OH−], [H2CO3], [HCO3 −], [CO3 2−]? No calculations are needed to answer this question.
- Calculate the concentration of each species present in a 0.050-M solution of H2S.
- Calculate the concentration of each species present in a 0.010-M solution of phthalic acid,C6H4(CO2H)2.C6H4(CO2H)2(aq) + H2O(l) ⇌ H3O+(aq)+C6H4(CO2H)(CO2)-(aq) Ka=1.1 x 10-3
C6H4(CO2H)(CO2)(aq) + H2O(l) ⇌ H3O+(aq) + C6H4(CO2)2 2-(aq) Ka= 3.9 x 10-6 - Salicylic acid, HOC6H4CO2H, and its derivatives have been used as pain relievers for a long time. Salicylic acid occurs in small amounts in the leaves, bark, and roots of some vegetation (most notably historically in the bark of the willow tree). Extracts of these plants have been used as medications for centuries. The acid was first isolated in the laboratory in 1838.
- Both functional groups of salicylic acid ionize in water, with Ka = 1.0 × 10−3 for the—CO2H group and 4.2 × 10−13 for the −OH group. What is the pH of a saturated solution of the acid (solubility = 1.8 g/L).
- Aspirin was discovered as a result of efforts to produce a derivative of salicylic acid that would not be irritating to the stomach lining. Aspirin is acetylsalicylic acid, CH3CO2C6H4CO2H. The −CO2H functional group is still present, but its acidity is reduced, Ka = 3.0 × 10−4. What is the pH of a solution of aspirin with the same concentration as a saturated solution of salicylic acid (See Part a).
- The ion HTe− is an amphiprotic species; it can act as either an acid or a base.
- What is Ka for the acid reaction of HTe− with H2O?
- What is Kb for the reaction in which HTe− functions as a base in water?
- Demonstrate whether or not the second ionization of H2Te can be neglected in the calculation of [HTe−] in a 0.10 M solution of H2Te.
- Explain why a buffer can be prepared from a mixture of NH4Cl and NaOH but not from NH3 and NaOH.
- Explain why the pH does not change significantly when a small amount of an acid or a base is added to a solution that contains equal amounts of the acid H3PO4 and a salt of its conjugate base NaH2PO4.
- Explain why the pH does not change significantly when a small amount of an acid or a base is added to a solution that contains equal amounts of the base NH3 and a salt of its conjugate acid NH4Cl.
- What is [H3O+] in a solution of 0.25 M CH3CO2H and 0.030 M NaCH3CO2?
CH3CO2H(aq) + H2O(l) ⇌ H3O+(aq) + CH3CO2 −(aq) Ka = 1.8 × 10−5 - What is [H3O+] in a solution of 0.075 M HNO2 and 0.030 M NaNO2?HNO2(aq) + H2 O(l) ⇌ H3 O+(aq) + NO2 −(aq)Ka = 4.5 × 10−5
- What is [OH−] in a solution of 0.125 M CH3NH2 and 0.130 M CH3NH3Cl?
CH3 NH2(aq) + H2 O(l) ⇌ CH3 NH3 +(aq) + OH−(aq)Kb = 4.4 × 10−4 - What is [OH−] in a solution of 1.25 M NH3 and 0.78 M NH4NO3? NH3(aq) + H2 O(l) ⇌ NH4 +(aq) + OH−(aq)Kb = 1.8 × 10−5
- What is the effect on the concentration of acetic acid, hydronium ion, and acetate ion when the following are added to an acidic buffer solution of equal concentrations of acetic acid and sodium acetate:
- HCl
- KCH3CO2
- NaCl
- KOH
- CH3CO2H
- What is the effect on the concentration of ammonia, hydroxide ion, and ammonium ion when the following are added to a basic buffer solution of equal concentrations of ammonia and ammonium nitrate:
- KI
- NH3
- HI
- NaOH
- NH4Cl
- What will be the pH of a buffer solution prepared from 0.20 mol NH3, 0.40 mol NH4NO3, and just enough water to give 1.00 L of solution?
- Calculate the pH of a buffer solution prepared from 0.155 mol of phosphoric acid, 0.250 mole of KH2PO4, and enough water to make 0.500 L of solution.
- How much solid NaCH3CO2•3H2O must be added to 0.300 L of a 0.50-M acetic acid solution to give a buffer with a pH of 5.00? (Hint: Assume a negligible change in volume as the solid is added.)
- What mass of NH4Cl must be added to 0.750 L of a 0.100-M solution of NH3 to give a buffer solution with a pH of 9.26? (Hint: Assume a negligible change in volume as the solid is added.)
- A buffer solution is prepared from equal volumes of 0.200 M acetic acid and 0.600 M sodium acetate. Use 1.80 × 10−5 as Ka for acetic acid.
- What is the pH of the solution?
- Is the solution acidic or basic?
- What is the pH of a solution that results when 3.00 mL of 0.034 M HCl is added to 0.200 L of the original buffer?
- A 5.36–g sample of NH4Cl was added to 25.0 mL of 1.00 M NaOH and the resulting solution diluted to 0.100 L.
- What is the pH of this buffer solution?
- Is the solution acidic or basic?
- What is the pH of a solution that results when 3.00 mL of 0.034 M HCl is added to the solution?
- Explain how to choose the appropriate acid-base indicator for the titration of a weak base with a strong acid.
- Explain why an acid-base indicator changes color over a range of pH values rather than at a specific pH.
- Calculate the pH at the following points in a titration of 40 mL (0.040 L) of 0.100 M barbituric acid (Ka = 9.8 × 10−5) with 0.100 M KOH.
- no KOH added
- 20 mL of KOH solution added
- 39 mL of KOH solution added
- 40 mL of KOH solution added
- 41 mL of KOH solution added
- The indicator dinitrophenol is an acid with a Ka of 1.1 × 10−4. In a 1.0 × 10−4-M solution, it is colorless in acid and yellow in base. Calculate the pH range over which it goes from 10% ionized (colorless) to 90% ionized (yellow).

