Precipitation and Dissolution (15.1)
Learning Objectives
By the end of this section, you will be able to:
- Write chemical equations and equilibrium expressions representing solubility equilibria
- Carry out equilibrium computations involving solubility, equilibrium expressions, and solute concentrations
Solubility equilibria are established when the dissolution and precipitation of a solute species occur at equal rates. These equilibria underlie many natural and technological processes, ranging from tooth decay to water purification. An understanding of the factors affecting compound solubility is, therefore, essential to the effective management of these processes. This section applies previously introduced equilibrium concepts and tools to systems involving dissolution and precipitation.
Preview video
The Solubility Product
Recall from the chapter on solutions that the solubility of a substance can vary from essentially zero (insoluble or sparingly soluble) to infinity (miscible). A solute with finite solubility can yield a saturated solution when it is added to a solvent in an amount exceeding its solubility, resulting in a heterogeneous mixture of the saturated solution and the excess, undissolved solute. For example, a saturated solution of silver chloride is one in which the equilibrium shown below has been established.
[latex]\text{AgCl}(s)\;\underset{\text{precipitation}}{\overset{\text{dissolution}}{\rightleftharpoons}}\;\text{Ag}^{+}(aq)\;+\;\text{Cl}^{-}(aq)[/latex]
In this solution, an excess of solid AgCl dissolves and dissociates to produce aqueous Ag+ and Cl– ions at the same rate that these aqueous ions combine and precipitate to form solid AgCl (Figure 15.2). Because silver chloride is a sparingly soluble salt, the equilibrium concentration of its dissolved ions in the solution is relatively low.
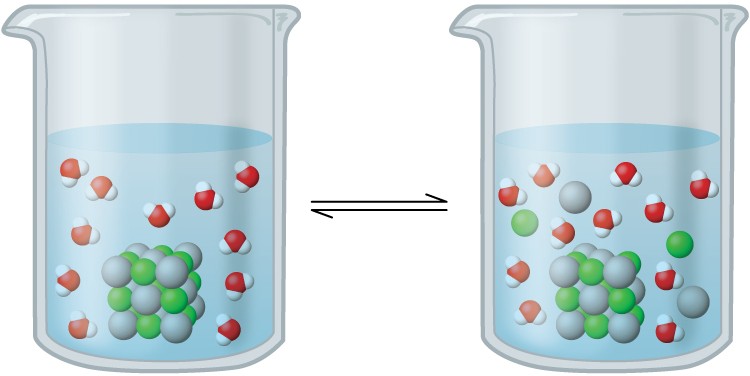
Figure 15.2 Silver chloride is a sparingly soluble ionic solid. When it is added to water, it dissolves slightly and produces a mixture consisting of a very dilute solution of Ag+ and Cl– ions in equilibrium with undissolved silver chloride.
The equilibrium constant for solubility equilibria such as this one is called the solubility product constant, Ksp, in this case
AgCl(s) ⇌ Ag+(aq) + Cl−(aq) Ksp = [Ag+(aq)][Cl−(aq)]
Recall that only gases and solutes are represented in equilibrium constant expressions, so the Ksp does not include a term for the undissolved AgCl. A listing of solubility product constants for several sparingly soluble compounds is provided in Appendix J.
Example 15.1
Writing Equations and Solubility Products
Write the dissolution equation and the solubility product expression for each of the following slightly soluble ionic compounds:
(a) AgI, silver iodide, a solid with antiseptic properties
(b) CaCO3, calcium carbonate, the active ingredient in many over-the-counter chewable antacids
(c) Mg(OH)2, magnesium hydroxide, the active ingredient in Milk of Magnesia
(d) (NH4)PO4, magnesium ammonium phosphate, an essentially insoluble substance used in tests for magnesium
(e) MgCa5(PO4)3OH, the mineral apatite, a source of phosphate for fertilizers
Solution
(a) AgI(s) ⇌ Ag+(aq) + I−(aq)
Ksp = [Ag+][I-]
(b) CaCO3(s) ⇌ Ca2+(aq) + CO3 2−(aq)
Ksp =[Ca2+][CO3 2-]
(c) Mg(OH)2(s) ⇌ Mg2+(aq) + 2OH−(aq)
Ksp =[Mg2+][OH-]2
(d) Mg(NH4)PO4(s) ⇌ Mg2+(aq) + NH4 +(aq) + PO4 3−(aq)
Ksp =[Mg2+][NH4 +][PO4 3-]
(e) Ca5(PO4)3OH(s) ⇌ 5Ca2+(aq) + 3PO4 3−(aq) + OH−(aq)
Ksp =[Ca2+]5[PO4 3-]3[OH -]
Check Your Learning
Write the dissolution equation and the solubility product for each of the following slightly soluble compounds:
(a) BaSO4
(b) Ag2SO4
(c) Al(OH)3
(d) Pb(OH)Cl
Answers:
(a) BaSO4(s) ⇌ Ba2+(aq) + SO42−(aq) Ksp = [Ba2+][SO4 2−];
(b) Ag2 SO4(s) ⇌ 2Ag+(aq) + SO42−(aq) Ksp = [Ag+]2[SO42−];
(c) Al(OH)3(s) ⇌ Al3+(aq) + 3OH−(aq) Ksp = [Al3+][OH− ]3;
(d) Pb(OH)Cl(s) ⇌ Pb2+(aq) + OH−(aq) + Cl−(aq) Ksp = [Pb2+][OH−][Cl−]
Ksp and Solubility
The Ksp of a slightly soluble ionic compound may be simply related to its measured solubility provided the dissolution process involves only dissociation and solvation, for example:
Mp Xq(s) ⇌ pMm+(aq) + qXn−(aq)
For cases such as these, one may derive Ksp values from provided solubilities, or vice-versa. Calculations of this sort are most conveniently performed using a compound’s molar solubility, measured as moles of dissolved solute per liter of saturated solution.
Example 15.2
Calculation of Ksp from Equilibrium Concentrations
Fluorite, CaF2, is a slightly soluble solid that dissolves according to the equation:
CaF2(s) ⇌ Ca2+(aq) + 2F−(aq)
The concentration of Ca2+ in a saturated solution of CaF2 is 2.15 × 10–4 M. What is the solubility product of fluorite?
Solution
According to the stoichiometry of the dissolution equation, the fluoride ion molarity of a CaF2 solution is equal to twice its calcium ion molarity:
[F− ] = (2 mol F− / 1 mol Ca 2+ ) = (2)(2.15 × 10−4 M) = 4.30 × 10−4
Substituting the ion concentrations into the Ksp expression gives
Ksp = [Ca2+][F−]2 = (2.15 × 10−4)(4.30 × 10−4)2 = 3.98 × 10−11
Check Your Learning
In a saturated solution of Mg(OH)2, the concentration of Mg2+ is 1.31 × 10–4 M. What is the solubility product for Mg(OH)2?
Mg(OH)2(s) ⇌ Mg2+(aq) + 2OH−(aq)
Answer: 8.99 × 10–12 M
Example 15.3
Determination of Molar Solubility from Ksp
The Ksp of copper(I) bromide, CuBr, is 6.3 × 10–9. Calculate the molar solubility of copper bromide.
Solution
The dissolution equation and solubility product expression are:
CuBr(s) ⇌ Cu+(aq) + Br−(aq)
Ksp = [Cu+][Br−]
Following the ICE approach to this calculation yields the table
| CuBr (s) | ⇌ | Cu+(aq) | + | Br-(aq) |
|---|
| Initial Concentration (M) | 0 | 0 | |
|---|---|---|---|
| Change (M) | +x | +x | |
| Equilibrium Concentration (M) | x | x |
Substituting the equilibrium concentration terms into the solubility product expression and solving for x yields:
Ksp = [Cu+][Br−]
6.3 × 10−9 = (x)(x) = x2
x =[latex]\sqrt{(6.3 \times 10^{−9})}[/latex] = 7.9 × 10−5 M
Since the dissolution stoichiometry shows one mole of copper(I) ion and one mole of bromide ion are produced for each moles of Br dissolved, the molar solubility of CuBr is 7.9 × 10–5 M.
Check Your Learning
The Ksp of AgI is 1.5 × 10–16. Calculate the molar solubility of silver iodide.
Answer: 1.2 × 10–8 M
Example 15.4
Determination of Molar Solubility from Ksp
The Ksp of calcium hydroxide, Ca(OH)2, is 1.3 × 10–6. Calculate the molar solubility of calcium hydroxide.
Solution
The dissolution equation and solubility product expression are
Ca(OH)2(s) ⇌ Ca2+(aq) + 2OH−(aq)
Ksp = [Ca2+][OH−]2
The ICE table for this system is:

Substituting terms for the equilibrium concentrations into the solubility product expression and solving for x gives
Ksp = [Ca2+][OH−]2
1.3 × 10−6 = (x)(2x)2 = (x)(4x2) = 4x3
x = [latex]^{3}\sqrt{\frac{1.3 \times 10^{-6}}{4}}[/latex] = 7.0 x 10-3 M
As defined in the ICE table, x is the molarity of calcium ion in the saturated solution. The dissolution stoichiometry shows a 1:1 relation between moles of calcium ion in solution and moles of compound dissolved, and so, the molar solubility of Ca(OH)2 is 6.9 × 10–3 M.
Check Your Learning
The Ksp of PbI2 is 1.4 × 10–8. Calculate the molar solubility of lead(II) iodide.
Answer: 1.5 × 10–3 M
Example 15.5
Determination of Ksp from Gram Solubility
Many of the pigments used by artists in oil-based paints (Figure 15.3) are sparingly soluble in water. For example, the solubility of the artist’s pigment chrome yellow, PbCrO4, is 4.6 × 10–6 g/L. Determine the solubility product for PbCrO4.
Figure 15.3 Oil paints contain pigments that are very slightly soluble in water. In addition to chrome yellow (PbCrO4), examples include Prussian blue (Fe7(CN)18), the reddish-orange color vermilion (HgS), and green color veridian (Cr2O3). (credit: Sonny Abesamis)
Solution
Before calculating the solubility product, the provided solubility must be converted to molarity:
[PbCrO4] = [latex]\frac{4.6 \times 10^{-6} \text{g PbCrO}_{4}}{1 \text{L}} \times \frac{1 \text{mol } \text{PbCrO}_{4}}{323.2 \text{g PbCrO}_{4}}[/latex]
= [latex]\frac{1.4 \times 10^{-8} \text{g mol } \text{PbCrO}_{4}}{1 \text{L}}[/latex]
= 1.4 x 10-8 M
The dissolution equation for this compound is
PbCrO4(s) ⇌ Pb2+(aq) + CrO4 2−(aq)
The dissolution stoichiometry shows a 1:1 relation between the molar amounts of compound and its two ions, and so both [Pb2+] and [CrO4 2−] are equal to the molar solubility of PbCrO4:
[Pb2+] = [CrO4 2−] = 1.4 × 10−8 M
Ksp = [Pb2+] [CrO4 2−] = (1.4 × 10–8)(1.4 × 10–8) = 2.0 × 10–16
Check Your Learning
The solubility of TlCl [thallium(I) chloride], an intermediate formed when thallium is being isolated from ores, is 3.12 grams per liter at 20 °C. What is its solubility product?
Answer: 2.08 × 10–4
Example 15.6
Calculating the Solubility of Hg2Cl2
Calomel, Hg2Cl2, is a compound composed of the diatomic ion of mercury(I), Hg2 2+, and chloride ions, Cl–. Although most mercury compounds are now known to be poisonous, eighteenth-century physicians used calomel as a medication. Their patients rarely suffered any mercury poisoning from the treatments because calomel has a very low solubility, as suggested by its very small Ksp:
Hg2 Cl2(s) ⇌ Hg2 2+(aq) + 2Cl−(aq)
Ksp = 1.1 × 10−18
Calculate the molar solubility of Hg2Cl2.
Solution
The dissolution stoichiometry shows a 1:1 relation between the amount of compound dissolved and the amount of mercury(I) ions, and so the molar solubility of Hg2Cl2 is equal to the concentration of Hg2 2+ ions
Following the ICE approach results in:

h g sub 2, C l sub 2, ( S ). Left and right reaction arrows. H g sub 2, to the power of 2 positive, ( a q ). plus 2 C l to the negative power, ( a q )
Substituting the equilibrium concentration terms into the solubility product expression and solving for x gives:
Ksp = [Hg2 2+][Cl−]2
1.1 × 10−18 = (x)(2x)2
4x3 = 1.1 x 10-18
x = [latex]^{3}\sqrt{( \frac{1.1 \times 10^{-18}}{4})}[/latex] = 6.5 x 10-7 M
[Hg2 2+] = 6.5 x 10-7 M = 6.5 x 10-7 M
[Cl-] = 2x = 2(6.5 x 10-7) = 1.3 x 10-6 M
The dissolution stoichiometry shows the molar solubility of Hg2Cl2 is equal to [Hg2 2+], or
6.5 × 10–7 M.
Check Your Learning
Determine the molar solubility of MgF2 from its solubility product: Ksp = 6.4 × 10–9.
Answer: 1.2 × 10–3
How Sciences Interconnect
Using Barium Sulfate for Medical Imaging
Various types of medical imaging techniques are used to aid diagnoses of illnesses in a noninvasive manner. One such technique utilizes the ingestion of a barium compound before taking an X-ray image. A suspension of barium sulfate, a chalky powder, is ingested by the patient. Since the Ksp of barium sulfate is 2.3 × 10–8, very little of it dissolves as it coats the lining of the patient’s intestinal tract. Barium-coated areas of the digestive tract then appear on an X-ray as white, allowing for greater visual detail than a traditional X-ray ( Figure 15.4).
Figure 15.4 A suspension of barium sulfate coats the intestinal tract, permitting greater visual detail than a traditional X-ray. (credit modification of work by “glitzy queen00”/Wikimedia Commons)
Medical imaging using barium sulfate can be used to diagnose acid reflux disease, Crohn’s disease, and ulcers in addition to other conditions.
Visit this website for more information on how barium is used in medical diagnoses and which conditions it is used to diagnose.
Predicting Precipitation
The equation that describes the equilibrium between solid calcium carbonate and its solvated ions is:
CaCO3(s) ⇌ Ca2+(aq) + CO32−(aq) Ksp = [Ca2 + ][CO32 − ] = 8.7 × 10−9
It is important to realize that this equilibrium is established in any aqueous solution containing Ca2+ and CO32– ions, not just in a solution formed by saturating water with calcium carbonate. Consider, for example, mixing aqueous solutions of the soluble compounds sodium carbonate and calcium nitrate. If the concentrations of calcium and carbonate ions in the mixture do not yield a reaction quotient, Qsp, that exceeds the solubility product, Ksp, then no precipitation will occur. If the ion concentrations yield a reaction quotient greater than the solubility product, then precipitation will occur, lowering those concentrations until equilibrium is established (Qsp = Ksp). The comparison of Qsp to Ksp to predict precipitation is an example of the general approach to predicting the direction of a reaction first introduced in the chapter on equilibrium. For the specific case of solubility equilibria:
Qsp < Ksp: the reaction proceeds in the forward direction (solution is not saturated; no precipitation observed) Qsp > Ksp: the reaction proceeds in the reverse direction (solution is supersaturated; precipitation will occur) This predictive strategy and related calculations are demonstrated in the next few example exercises.
Example 15.7
Precipitation of Mg(OH)2
The first step in the preparation of magnesium metal is the precipitation of Mg(OH)2 from sea water by the addition of lime, Ca(OH)2, a readily available inexpensive source of OH– ion:
Mg(OH)2(s) ⇌ Mg2+(aq) + 2OH−(aq)
Ksp = 8.9 × 10−12
The concentration of Mg2+(aq) in sea water is 0.0537 M. Will Mg(OH)2 precipitate when enough Ca(OH)2 is added to give a [OH–] of 0.0010 M?
Solution
Calculation of the reaction quotient under these conditions is shown here:
Q = [Mg2+][OH−]2 = (0.0537)(0.0010)2 = 5.4 × 10−8
Because Q is greater than Ksp (Q = 5.4 × 10–8 is larger than Ksp = 8.9 × 10–12), the reverse reaction will proceed, precipitating magnesium hydroxide until the dissolved ion concentrations have been sufficiently lowered, so that Qsp = Ksp.
Check Your Learning
Predict whether CaHPO4 will precipitate from a solution with [Ca2+] = 0.0001 M and [HPO42−] = 0.001M.
Answer: No precipitation of CaHPO4; Q = 1 × 10–7, which is less than Ksp (7 × 10–7)
Example 15.8
Precipitation of AgCl
Does silver chloride precipitate when equal volumes of a 2.0 × 10–4 M solution of AgNO3 and a 2.0 ×10–4 M solution of NaCl are mixed?
Solution
The equation for the equilibrium between solid silver chloride, silver ion, and chloride ion is:
AgCl(s) ⇌ Ag+(aq) + Cl−(aq)
The solubility product is 1.6 × 10–10 (see Appendix J).
AgCl will precipitate if the reaction quotient calculated from the concentrations in the mixture of AgNO3 and NaCl is greater than Ksp. Because the volume doubles when equal volumes of AgNO3 and NaCl solutions are mixed, each concentration is reduced to half its initial value
[latex]\frac{1}{2}[/latex](2.0 x 10-4) M = 1.0 x 10-4 M
The reaction quotient, Q, is greater than Ksp for AgCl, so a supersaturated solution is formed:
Q = [Ag+][Cl−] = (1.0 × 10−4)(1.0 × 10−4) = 1.0 × 10−8 > Ksp
AgCl will precipitate from the mixture until the dissolution equilibrium is established, with Q equal to Ksp.
Check Your Learning
Will KClO4 precipitate when 20 mL of a 0.050-M solution of K+ is added to 80 mL of a 0.50-M solution of ClO4 − ? (Hint: Use the dilution equation to calculate the concentrations of potassium and perchlorate ions in the mixture.)
Answer: No, Q = 4.0 × 10–3, which is less than Ksp = 1.05 × 10–2
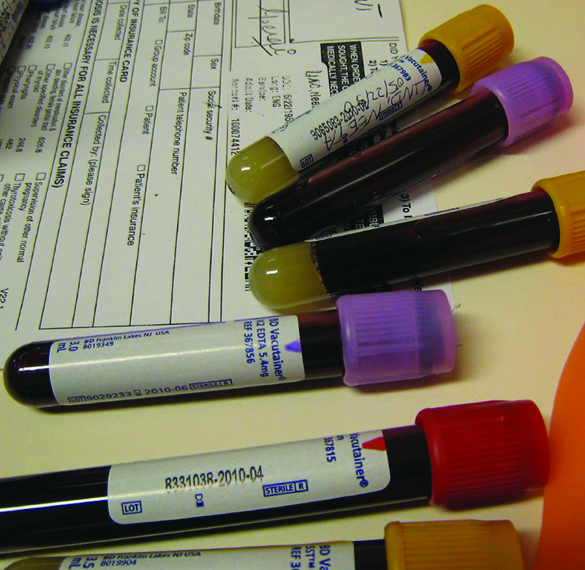
Example 15.9
Precipitation of Calcium Oxalate
Blood will not clot if calcium ions are removed from its plasma. Some blood collection tubes contain salts of the oxalate ion, C2O4 2−, for this purpose (Figure 15.5). At sufficiently high concentrations, the calcium and oxalate ions form solid, CaC2O4∙H2O (calcium oxalate monohydrate). The concentration of Ca2+ in a sample of blood serum is 2.2 × 10–3 M. What concentration of C2O4 2− ion must be established before CaC2O4∙H2O begins to precipitate?
Figure 15.5 Anticoagulants can be added to blood that will combine with the Ca2+ ions in blood serum and prevent the blood from clotting. (credit: modification of work by Neeta Lind)
Solution
The equilibrium expression is:
CaC2O4(s) ⇌ Ca2+(aq) + C2O42−(aq)
For this reaction:
Ksp = [Ca2+][C2O42−] = 1.96 × 10−8
(see Appendix J)
Substitute the provided calcium ion concentration into the solubility product expression and solve for oxalate concentration:
Q = Ksp = [Ca2+][C2O42−] = 1.96 × 10−8
(2.2 × 10−3)[C2O42−] = 1.96 × 10−8
[C2O42−] = [latex]\frac{1.96 \times 10^{-8}}{2.2 \times 10^{-3}}[/latex] = 8.9 x 10-6
A concentration of [C2O42−] = 8.9 × 10–6 M is necessary to initiate the precipitation of CaC2O4 under these conditions.
Check Your Learning
If a solution contains 0.0020 mol of CrO42− per liter, what concentration of Ag+ ion must be reached by adding solid AgNO3 before Ag2CrO4 begins to precipitate? Neglect any increase in volume upon adding the solid silver nitrate.
Answer: 6.7 × 10–5 M
Example 15.10
Concentrations Following Precipitation
Clothing washed in water that has a manganese [Mn2+(aq)] concentration exceeding 0.1 mg/L (1.8 × 10–6M) may be stained by the manganese upon oxidation, but the amount of Mn2+ in the water can be decreased by adding a base to precipitate Mn(OH)2. What pH is required to keep [Mn2+] equal to 1.8 × 10–6 M?
Solution
The dissolution of Mn(OH)2 is described by the equation:
Mn(OH)2(s) ⇌ Mn2+(aq) + 2OH−(aq) Ksp = 2 × 10−13
At equilibrium:
Ksp = [Mn2+][OH−]2
or
(1.8 × 10−6)[OH−]2 = 2 × 10−13
so
[OH−] = 3.3 × 10−4 M
Calculate the pH from the pOH:
pOH = −log[OH−] = −log(3.3 × 10 − 4) = 3.48
pH = 14.00 − pOH = 14.00 − 3.80 = 10.5
(final result rounded to one significant digit, limited by the certainty of the Ksp)
Check Your Learning
The first step in the preparation of magnesium metal is the precipitation of Mg(OH)2 from sea water by the addition of Ca(OH)2. The concentration of Mg2+(aq) in sea water is 5.37 × 10–2 M. Calculate the pH at which [Mg2+] is decreased to 1.0 × 10–5 M
Answer: 10.97
In solutions containing two or more ions that may form insoluble compounds with the same counter ion, an experimental strategy called selective precipitation may be used to remove individual ions from solution. By increasing the counter ion concentration in a controlled manner, ions in solution may be precipitated individually, assuming their compound solubilities are adequately different. In solutions with equal concentrations of target ions,
the ion forming the least soluble compound will precipitate first (at the lowest concentration of counter ion), with the other ions subsequently precipitating as their compound’s solubilities are reached. As an illustration of this technique, the next example exercise describes separation of a two halide ions via precipitation of one as a silver salt.
Chemistry in Everyday Life
The Role of Precipitation in Wastewater Treatment
Solubility equilibria are useful tools in the treatment of wastewater carried out in facilities that may treat the municipal water in your city or town (Figure 15.6). Specifically, selective precipitation is used to remove contaminants from wastewater before it is released back into natural bodies of water. For example, phosphate
ions (PO4 3−) are often present in the water discharged from manufacturing facilities. An abundance of
phosphate causes excess algae to grow, which impacts the amount of oxygen available for marine life as well as making water unsuitable for human consumption
Figure 15.6 Wastewater treatment facilities, such as this one, remove contaminants from wastewater before the water is released back into the natural environment. (credit: “eutrophication&hypoxia”/Wikimedia Commons)
One common way to remove phosphates from water is by the addition of calcium hydroxide, or lime, Ca(OH)2. As the water is made more basic, the calcium ions react with phosphate ions to produce hydroxylapatite, Ca5(PO4)3OH, which then precipitates out of the solution:
5Ca2+ + 3PO43− + OH− ⇌ Ca5 (PO4)3 ·OH(s)
Because the amount of calcium ion added does not result in exceeding the solubility products for other calcium salts, the anions of those salts remain behind in the wastewater. The precipitate is then removed by filtration and the water is brought back to a neutral pH by the addition of CO2 in a recarbonation process. Other chemicals can also be used for the removal of phosphates by precipitation, including iron(III) chloride and aluminum sulfate.
View this site for more information on how phosphorus is removed from wastewater.
Example 15.11
Precipitation of Silver Halides
A solution contains 0.00010 mol of KBr and 0.10 mol of KCl per liter. AgNO3 is gradually added to this solution. Which forms first, solid AgBr or solid AgCl?
Solution
The two equilibria involved are:
AgCl(s) ⇌ Ag+(aq) + Cl−(aq) Ksp = 1.6 × 10−10
AgBr(s) ⇌ Ag+(aq) + Br−(aq) Ksp = 5.0 × 10−13
If the solution contained about equal concentrations of Cl– and Br–, then the silver salt with the smaller Ksp (AgBr) would precipitate first. The concentrations are not equal, however, so the [Ag+] at which AgCl begins to precipitate and the [Ag+] at which AgBr begins to precipitate must be calculated. The salt that forms at the lower [Ag+] precipitates first.
AgBr precipitates when Q equals Ksp for AgBr
Q = [Ag+][Br−] = [Ag+](0.00010) = 5.0 × 10−13
[Ag+] = [latex]\frac{5.0 \times 10^{-13}}{0.00010}[/latex] = 5.0 x 10-9 M
AgI begins to precipitate when [Ag+] is 5.0 × 10–9 M.
For AgCl: AgCl precipitates when Q equals Ksp for AgCl (1.6 × 10–10). When [Cl–] = 0.10 M:
Qsp = [Ag+][Cl−] = [Ag+](0.10) = 1.6 × 10−10
[Ag +] = [latex]\frac{1.6 \times 10^{-10}}{0.10}[/latex] = 1.6 x 10-9 M
AgCl begins to precipitate when [Ag+] is 1.6 × 10–9 M.
AgCl begins to precipitate at a lower [Ag+] than AgBr, so AgCl begins to precipitate first. Note the chloride ion concentration of the initial mixture was significantly greater than the bromide ion concentration, and so silver chloride precipitated first despite having a Ksp greater than that of silver bromide.
Check Your Learning
If silver nitrate solution is added to a solution which is 0.050 M in both Cl– and Br– ions, at what [Ag+] would precipitation begin, and what would be the formula of the precipitate?
Answer: [Ag+] = 1.0 × 10–11 M; AgBr precipitates first
Common Ion Effect
Compared with pure water, the solubility of an ionic compound is less in aqueous solutions containing a common ion (one also produced by dissolution of the ionic compound). This is an example of a phenomenon known as the common ion effect, which is a consequence of the law of mass action that may be explained using Le ChÂtelier’s principle. Consider the dissolution of silver iodide:
AgI(s) ⇌ Ag+(aq) + I−(aq)
This solubility equilibrium may be shifted left by the addition of either silver(I) or iodide ions, resulting in the precipitation of AgI and lowered concentrations of dissolved Ag+ and I–. In solutions that already contain either of these ions, less AgI may be dissolved than in solutions without these ions.
This effect may also be explained in terms of mass action as represented in the solubility product expression:
Ksp = [Ag+ ][I−]
The mathematical product of silver(I) and iodide ion molarities is constant in an equilibrium mixture regardless of the source of the ions, and so an increase in one ion’s concentration must be balanced by a proportional decrease in the other.
Link to Learning
View this simulation to explore various aspects of the common ion effect.
View this simulation to see how the common ion effect workswith different concentrations of salts.
Example 15.12
Common Ion Effect on Solubility
What is the effect on the amount of solid Mg(OH)2 and the concentrations of Mg2+ and OH– when each of the following are added to a saturated solution of Mg(OH)2?
(a) MgCl2
(b) KOH
(c) NaNO3
(d) Mg(OH)2
Solution
The solubility equilibrium is
Mg(OH)2(s) ⇌ Mg2+(aq) + 2OH−(aq)
(a)The reaction shifts to the left to relieve the stress produced by the additional Mg2+ ion, in accordance with Le Châtelier’s principle. In quantitative terms, the added Mg2+ causes the reaction quotient to be larger than the solubility product (Q > Ksp), and Mg(OH)2 forms until the reaction quotient again equals Ksp. At the new equilibrium, [OH–] is less and [Mg2+] is greater than in the solution of Mg(OH)2 in pure water. More solid Mg(OH)2 is present.
(b)The reaction shifts to the left to relieve the stress of the additional OH– ion. Mg(OH)2 forms until the reaction quotient again equals Ksp. At the new equilibrium, [OH–] is greater and [Mg2+] is less than in the solution of Mg(OH)2 in pure water. More solid Mg(OH)2 is present.
(c)The concentration of OH– is reduced as the OH– reacts with the acid. The reaction shifts to the right to
(a) Adding a common ion, Mg2+, will increase the concentration of this ion and shift the solubility equilibrium to the left, decreasing the concentration of hydroxide ion and increasing the amount of undissolved magnesium hydroxide.
(b) Adding a common ion, OH–, will increase the concentration of this ion and shift the solubility equilibrium to the left, decreasing the concentration of magnesium ion and increasing the amount of undissolved magnesium hydroxide.
(c) The added compound does not contain a common ion, and no effect on the magnesium hydroxide solubility equilibrium is expected.
(d) Adding more solid magnesium hydroxide will increase the amount of undissolved compound in the mixture. The solution is already saturated, though, so the concentrations of dissolved magnesium and hydroxide ions will remain the same.
Q = [Mg2+][OH−]2
Thus, changing the amount of solid magnesium hydroxide in the mixture has no effect on the value of Q, and no shift is required to restore Q to the value of the equilibrium constant.
Check Your Learning
What is the effect on the amount of solid NiCO3 and the concentrations of Ni2+ and CO3 2− when each of the following are added to a saturated solution of NiCO3
(a) Ni(NO3)2
(b) KClO4
(c) NiCO3
(d) K2CO3
Answer:
(a) mass of NiCO3(s) increases, [Ni2+] increases, [CO3 2−] decreases;
(b) no appreciable effect;
(c) no effect except to increase the amount of solid NiCO3;
(d) mass of NiCO3(s) increases, [Ni2+] decreases,[CO3 2−] increases;
Example 15.13
Common Ion Effect
Calculate the molar solubility of cadmium sulfide (CdS) in a 0.010-M solution of cadmium bromide (CdBr2). The Ksp of CdS is 1.0 × 10–28.
Solution
This calculation can be performed using the ICE approach:
CdS(s) ⇌ Cd2+(aq) + S2−(aq)

Ksp = [Cd2+][S2−] = 1.0 × 10−28
(0.010 + x)(x) = 1.0 × 10−28
Because Ksp is very small, assume x << 0.010 and solve the simplified equation for x:
(0.010)(x) = 1.0 × 10−28
x = 1.0 × 10−26 M
The molar solubility of CdS in this solution is 1.0 × 10–26 M.
Check Your Learning
Calculate the molar solubility of aluminum hydroxide, Al(OH)3, in a 0.015-M solution of aluminum nitrate,
Al(NO3)3. The Ksp of Al(OH)3 is 2 × 10–32.
Answer: 4 × 10–11 M
A related story (Flint water crisis):
And the Chemistry behind the Flint water crisis: