1.5 The Time Value of Money I: Single Deposits
The Concept of the Time Value of Money
Personal Finance. Provided by: Saylor Academy. Located at: https://saylordotorg.github.io/text_personal-finance. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
Part of the planning process is evaluating the possible future results of a decision. Since those results will occur some time from now (i.e., in the future), it is critical to understand how time passing may affect those benefits and costs—not only the probability of their occurrence, but also their value when they do. Time affects value because time affects liquidity.
Liquidity is valuable, and the liquidity of an asset affects its value: all things being equal, the more liquid an asset is, the better. This relationship—how the passage of time affects the liquidity of money and thus its value—is commonly referred to as the time value of money[1], which can actually be calculated concretely as well as understood abstractly.
In general, transforming not-so-liquid wealth into liquid wealth creates transaction costs, opportunity costs, and risk, all of which take away from the value of wealth. Liquidity has value because it can be used without any additional costs.
One dimension of difference between not-so-liquid wealth and liquidity is time. Cash flows (CF) in the past are sunk, cash flows in the present are liquid, and cash flows in the future are not yet liquid. You can only make choices with liquid wealth, not with cash that you don’t have yet or that has already been spent. Separated from your liquidity and your choices by time, there is an opportunity cost: if you had liquidity now, you could use it for consumption or investment and benefit from it now. There is also risk, as there is always some uncertainty about the future: whether or not you will actually get your cash flows and just how much they’ll be worth when you do.
The further in the future cash flows are, the farther away you are from your liquidity, the more opportunity cost and risk you have, and the more that takes away from the present value (PV) of your wealth, which is not yet liquid. In other words, time puts distance between you and your liquidity, and that creates costs that take away from value. The more time there is, the larger its effect on the value of wealth.
Financial plans are expected to happen in the future, so financial decisions are based on values some distance away in time. You could be trying to project an amount at some point in the future—perhaps an investment payout or college tuition payment. Or perhaps you are thinking about a series of cash flows that happen over time—for example, annual deposits into and then withdrawals from a retirement account. To really understand the time value of those cash flows, or to compare them in any reasonable way, you have to understand the relationships between the nominal or face values in the future and their equivalent, present values (i.e., what their values would be if they were liquid today). The equivalent present values today will be less than the nominal or face values in the future because that distance over time, that separation from liquidity, costs us by discounting those values.
Financial calculation is not often a necessary skill since it is easier to use calculators, spreadsheets, and software. However, understanding the calculations is important in understanding the relationships between time, risk, opportunity cost, and value.
To do the math, you need to know
- what the future cash flows (CF) will be,
- when the future cash flows will be,
- the rate at which time affects value (e.g., the costs per time period, or the magnitude [the size or amount] of the effect of time on value).
At times, the alternatives are clear: you could be putting the liquidity in an account earning 3 percent, so that’s your opportunity cost of not having it. Or you are paying 6.5 percent on a loan, which you wouldn’t be paying if you had enough liquidity to avoid having to borrow; so that’s your opportunity cost. Sometimes, however, your opportunity cost is not so clear.
Say that today is your twentieth birthday. Your grandparents have promised to give you ![]() 1,000 for your twenty-first birthday, one year from today. If you had the money today, what would it be worth? That is, how much would
1,000 for your twenty-first birthday, one year from today. If you had the money today, what would it be worth? That is, how much would ![]() 1,000 worth of liquidity one year from now be worth today?
1,000 worth of liquidity one year from now be worth today?
That depends on the cost of its not being liquid today, or on the opportunity costs and risks created by not having liquidity today. If you had ![]() 1,000 today, you could buy things and enjoy them, or you could deposit it in an interest-bearing account. So on your twenty-first birthday, you would have more than
1,000 today, you could buy things and enjoy them, or you could deposit it in an interest-bearing account. So on your twenty-first birthday, you would have more than ![]() 1,000. You would have the
1,000. You would have the ![]() 1,000 plus whatever interest it had earned. If your bank pays 4 percent per year (interest rates are always stated as annual rates) on your account, then you would earn
1,000 plus whatever interest it had earned. If your bank pays 4 percent per year (interest rates are always stated as annual rates) on your account, then you would earn ![]() 40 of interest in the next year, or
40 of interest in the next year, or ![]() So on your twenty-first birthday you would have
So on your twenty-first birthday you would have ![]() 1,040.
1,040.
![]()
If you left that amount in the bank until your twenty-second birthday, you would have
![]()
To generalize the computation, if your present value[2], or PV, is your value today, r is the rate at which time affects value or discount rate (in this case, your interest rate), and if t is the number of time periods between you and your liquidity, then the future value[3], or FV, for each year is shown below in Table 1.5.1.
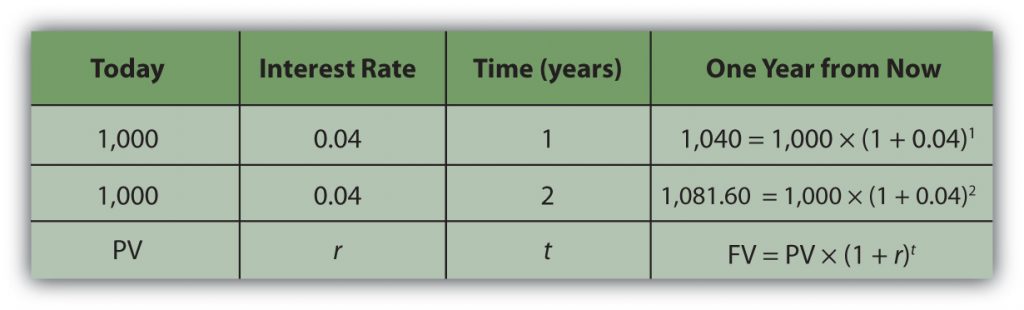
Calculating the Future Value of Money
College Algebra. Provided by: OpenStax. Located at: https://openstax.org/books/college-algebra/pages/6-1-exponential-functions
Savings instruments in which earnings are continually reinvested, such as mutual funds and retirement accounts, use compound interest. The term compounding refers to interest earned not only on the original value, but on the accumulated value of the account.
Th annual percentage rate (APR) of an account, also called the nominal rate, is the yearly interest rate earned by an investment account. The term nominal is used when the compounding occurs a number of times other than once per year. In fact, when interest is compounded more than once a year, the effective interest rate ends up being greater than the nominal rate! This is a powerful tool for investing.
We can calculate the future value using the following formula:
![]()
In this equation, ![]() is the present value of money. We generally view this as the “starting” amount or initial investment though it does not always have to represent the starting value.
is the present value of money. We generally view this as the “starting” amount or initial investment though it does not always have to represent the starting value. ![]() is the future value of the money. In other words, how much is the
is the future value of the money. In other words, how much is the ![]() worth after
worth after ![]() years. The variable
years. The variable ![]() is the annual interest rate given as a decimal. So, for instance, if the annual interest rate is
is the annual interest rate given as a decimal. So, for instance, if the annual interest rate is ![]() we would use
we would use ![]() Finally,
Finally, ![]() is the number of compounding periods per year; that is, how many times to we add interest to the account each year? I discuss the concept of compounding periods below.
is the number of compounding periods per year; that is, how many times to we add interest to the account each year? I discuss the concept of compounding periods below.
Compounding Periods
Written by JZK
While the other variables are relatively straightforward, the concept of compounding periods tends to be a new concept for many students. Therefore, I discuss it more here.
If you have an account that pays 12% interest per year, do you receive a single 12% interest payment each year? Maybe. Maybe not. That would be part of the agreement that you have with the bank. What if you are paid quarterly (once every three months?) Instead of getting a single 12% interest payment, you would instead get four 3% interest payments. Or, what if you get interest once per month? In that case, you would get 12 1% interest payments. We account for this in the future value using the variable ![]() . The table below gives the compounding periods for different time periods. Simply put…how many times is interest accounted for each year?
. The table below gives the compounding periods for different time periods. Simply put…how many times is interest accounted for each year?
| Compounding Periods | n |
| Annual | 1 |
| Quarterly | 4 |
| Monthly | 12 |
| Daily | 365 |
We see the term in the equation is ![]() So essentially what we calculating the interest per period. Table 1.5.3 shows the interest paid per period if the annual interest rate is 12%.
So essentially what we calculating the interest per period. Table 1.5.3 shows the interest paid per period if the annual interest rate is 12%.
| Compounding Periods | n | r/n |
| Annual | 1 | 12/1=12% |
| Quarterly | 4 | 12/4=3% |
| Monthly | 12 | 12/12=1% |
| Daily | 365 | 12/365=.033% |
The final part of the equation is the exponent ![]() . While it is fine to just plug the value in, we can see that we are actually doing a per period calculation and not a per year calculation. For example, if we have a five-year period we are examining and interest compounds monthly, then there are
. While it is fine to just plug the value in, we can see that we are actually doing a per period calculation and not a per year calculation. For example, if we have a five-year period we are examining and interest compounds monthly, then there are ![]() or
or ![]() periods (since there are sixty months in five years.)
periods (since there are sixty months in five years.)
While we could easily talk more about the concepts, it is easiest to just jump into the problems!
Solving time value of money questions
Written by JZK
Finding Future Value
For these, we simply plug in the required values and solve. Remember you order of operations! Do the inside of the parentheses first, then the exponent, then multiply by the value out in front.
Let’s try one together…
You deposit ![]() 25,000 into a savings account that pays 8% per year compounded monthly. Calculate the balance after 15 years assuming no additional deposits are made.
25,000 into a savings account that pays 8% per year compounded monthly. Calculate the balance after 15 years assuming no additional deposits are made.
Answer: 82,673
Let’s try one together…
You borrow ![]() 50,000 at a rate of 4% per year compounded monthly. As part of the agreement, you do not have to make any payments for 3 years but interest will accrue during that time. How much will you owe after 3 years assuming you make no payments on the money you borrowed.
50,000 at a rate of 4% per year compounded monthly. As part of the agreement, you do not have to make any payments for 3 years but interest will accrue during that time. How much will you owe after 3 years assuming you make no payments on the money you borrowed.
Answer: 56,364
Finding Present Value
This is also algebraic. Because present value is only multiplied by the larger term, all we need to do is plug in future value and the numbers into the larger multiplier term and then divide.
Let’s try one together…
Bob has a savings account currently worth ![]() 35,440.63. He made one initial deposit five years ago. The account pays 7% interest compounded monthly. How much did Bob initially deposit?
35,440.63. He made one initial deposit five years ago. The account pays 7% interest compounded monthly. How much did Bob initially deposit?
Answer: 25,000
Let’s try one together…
Tianyue currently owes ![]() 53,933.94 from a loan she took our 10 years ago. She has yet to make a payment on the loan. She received the proceeds of the loan in one single disbursement. The loan comes at a rate of 3% and is compounded quarterly. What is the principal of the loan?
53,933.94 from a loan she took our 10 years ago. She has yet to make a payment on the loan. She received the proceeds of the loan in one single disbursement. The loan comes at a rate of 3% and is compounded quarterly. What is the principal of the loan?
Answer: 40,000
Finding Interest Rate
To find the number of years, we will need to use fractional exponents. We will not go over this other than how to input it into our calculators. For these problems, we have three steps:
- Divide both sides by the future value.
- Take the reciprocal root. For example, if the parentheses are raised to the 10th power, you will raise both sides to the 1/10 power.
- Subtract by 1.
- Multiply by
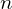 .
.
Again, it is much easier to see how to do this through an example.
Let’s try one together…
Answer: 8%
Let’s try one together…
You deposit ![]() 7,500 into an account. After 10 years, the account is worth
7,500 into an account. After 10 years, the account is worth ![]() 44,187.02. If the interest compounds quarterly, calculate the annual interest rate.
44,187.02. If the interest compounds quarterly, calculate the annual interest rate.
Answer: 18.13%
Finding the Number of Years
If we recall the formula from earlier, we see that the ![]() variable which represents the number of years is in the exponent. As we saw in the previous section, we need to use logs to solve for a variable in the exponent. The steps for this process are:
variable which represents the number of years is in the exponent. As we saw in the previous section, we need to use logs to solve for a variable in the exponent. The steps for this process are:
- Divide both sides by the present value.
- Take the log of both sides with the base being the exponent.
- Evaluate the innards of the multiplier term.
- Divide both sides by the result of the innards.
Again, it is much easier to see how to do this through an example.
Let’s try one together…
Francisca deposits ![]() 15,000 into an account. After a certain number of years, the account is worth
15,000 into an account. After a certain number of years, the account is worth ![]() 220,959. If the account pays 9% compounded monthly, how long has the money been in the account?
220,959. If the account pays 9% compounded monthly, how long has the money been in the account?
Answer: 30 years
Let’s try one together…
Answer: 8 years
https://youtu.be/3q5Da45Ip18
Finding the Number of Compounding Periods
Good news…we will not solve for these!
Discrete versus continuous growth
In the previous sections we examined discrete growth. Discrete periods are countable periods such as years, quarters, months, days, or even minutes or seconds. But what if we split time into smaller and smaller units like milliseconds, nanoseconds, or the newly measured zeptosecond (measured by the Germans this year) which is 0.000000000000000000001 second. Eventually we move out of the world of discrete math and into the world of continuous math where there are no longer separate time units and instead one single continuum of time. If you have had calculus, this is where the concept of the infintesimal comes from!
Due to its limited use in real world personal finance, we will not go any further with the continuous space. If we did, we would talk about the number “e”. You may have seen this discussed in math classes, but we will not cover it here.
Let us imagine that we have a single dollar that we place into a savings account. The account pays 100% (remember, as a decimal, 100%=1.0) annual interest. We want to know how much the account will be worth after 1 year. Let us take a took at the value of the account using different compounding periods:
Compounds Annually (![]() )
)
![]()
Compounds Semi-Annually (![]() )
)
![]()
Compounds Quarterly (![]() )
)
![]()
Compounds Monthly (![]() )
)
![]()
Compounds Daily (![]() )
)
![]()
Compounds Hourly (![]() )
)
![]()
Compounds Once per Minute (![]() )
)
![]()
Compounds Once per Second (![]() )
)
![]()
Even though the annual interest rate is the same, money grows faster the more frequently it is compounded. This again gets back to the idea of interest earning interest. The earlier interest is added to an account, the sooner it can start to earn interest and have that interest start to earn money, etc. This is great for savings but bad for debt. As we will soon find out, savings accounts are generally compounded monthly whereas credit cards are compounded daily!
The Rule of 72
From: https://en.wikipedia.org/wiki/Rule_of_72 (CC-BY)
In finance, the rule of 72, the rule of 70[1] and the rule of 69.3 are methods for estimating an investment‘s doubling time. The rule number (e.g., 72) is divided by the interest percentage per period (usually years) to obtain the approximate number of periods required for doubling. Although scientific calculators and spreadsheet programs have functions to find the accurate doubling time, the rules are useful for mental calculations and when only a basic calculator is available.[2]
These rules apply to exponential growth and are therefore used for compound interest as opposed to simple interest calculations. They can also be used for decay to obtain a halving time. The choice of number is mostly a matter of preference: 69 is more accurate for continuous compounding, while 72 works well in common interest situations and is more easily divisible. There is a number of variations to the rules that improve accuracy.
Let us use the continuous growth model to determine how long a quantity takes to double. In this case, the future value will just be double the present value, so ![]() . Therefore, we have:
. Therefore, we have:
![]() .
.
Dividing both sides by ![]() , we get
, we get
![]() .
.
We then take the natural log of both sides to get
![]()
To solve for ![]() , we can divide both sides by
, we can divide both sides by ![]() to get
to get
![]()
Since ![]() is given a decimal, we can multiply it by 100 to use it as a whole number. Since we are multiplying the denominator by 100, we must also multiply the numerator by 100:
is given a decimal, we can multiply it by 100 to use it as a whole number. Since we are multiplying the denominator by 100, we must also multiply the numerator by 100:
![]()
As mentioned earlier, we use 72 because this method is only an approximation and 72 divides much better (72 is divisible by 2, 3, 4, 6, 8, 9, 12,…). Let us see how it works.
Let us try one together…
Mel has ![]() 500 in an account that pays 4% interest annually. Use the Rule of 72 to approximate how long will it take to have
500 in an account that pays 4% interest annually. Use the Rule of 72 to approximate how long will it take to have ![]() 1,000.
1,000. ![]() 2,000.
2,000. ![]() 4,000.
4,000.
Answers: 18 years, 36 years, 54 years
Effective interest rate
From: https://en.wikipedia.org/wiki/Effective_interest_rate (CC BY)
The effective interest rate (EIR), effective annual interest rate, annual equivalent rate (AER) or simply effective rate is the interest rate on a loan or financial product restated from the nominal interest rate and expressed as the equivalent interest rate if compound interest was payable annually in arrears.
It is used to compare the interest rates between loans with different compounding periods, such as weekly, monthly, half-yearly or yearly. The effective interest rate sometimes differs in one important respect from the annual percentage rate (APR): the APR method converts this weekly or monthly interest rate into what would be called an annual rate that (in some parts of the world) doesn’t take into account the effect of compounding.[1]
By contrast, in the EIR, the periodic rate is annualized using compounding. It is the standard in the European Union and many other countries around the world.
The EIR is precise in financial terms, because it allows for the effects of compounding, i.e. the fact that for each period, interest is not calculated on the principal, but on the amount accumulated at the end of the previous period, including capital and interest. This reasoning is easily understandable when looking at savings: if interest is capitalized every month, then in every month the saver earns interest on the entire sum, including interest from the previous period. Thus if one starts with ![]() 1000 and earns interest at 2% every month, the accumulated sum at the end of the year is
1000 and earns interest at 2% every month, the accumulated sum at the end of the year is ![]() 1268.24, giving an effective interest rate of about 26.8%, not 24%.
1268.24, giving an effective interest rate of about 26.8%, not 24%.
The term nominal EIR or nominal APR can (subject to legislation) be used to refer to an annualized rate that does not take into account front-fees and other costs can be included.
Annual percentage yield or effective annual yield is the analogous concept used for savings or investment products, such as a certificate of deposit. Since any loan is an investment product for the lender, the terms may be used to apply to the same transaction, depending on the point of view.
Effective annual interest or yield may be calculated or applied differently depending on the circumstances, and the definition should be studied carefully. For example, a bank may refer to the yield on a loan portfolio after expected losses as its effective yield and include income from other fees, meaning that the interest paid by each borrower may differ substantially from the bank’s effective yield.
The effective interest rate is calculated as if compounded annually. The effective rate is calculated in the following way, where r is the effective annual rate, i the nominal rate, and n the number of compounding periods per year (for example, 12 for monthly compounding):
![]()
For continuously compounding interest, we have
![]()
Let’s try one together…
PNC offers you a loan with an 8.55% annual interest rate compounded daily. Calculate the effective interest rate. Interpret the result.
Answer: 8.93%
Let’s Try One Together
You are looking to take out a $15,000 loan for home renovations. If you want to minimize the interest paid, which bank should you get the loan from?
- Ally quotes you a rate of 4.77% compounded annually
- Bank of America quotes you a rate of 4.68% compounded quarterly.
- Capital One quotes you a rate of 4.61% compounded daily.
Answers: EIRs = 4.77%, 4.76%, 4.71%; Choose Capital One

