Section 2.6 Linear Transformations

2.6A

Definition: A transformation (or mapping) [latex]T[/latex] is linear if

(1) [latex]T(\vec{u}+\vec{v}) = T(\vec{u}) + T(\vec{v})[/latex] for all [latex]\vec{u},\vec{v}[/latex] in the domain of [latex]T[/latex].

(2) [latex]T(c\vec{u}) = cT(\vec{u})[/latex] for all scalars [latex]c[/latex] and all [latex]\vec{u}[/latex] in the domain of [latex]T[/latex].

Fact: 1. Linear transformations preserve the operations of vector addition and scalar multiplication.

2. If [latex]T[/latex] is a linear transformation, then [latex]T(\vec{0}) = \vec{0}[/latex] and [latex]T(c\vec{u}+d\vec{v}) = cT(\vec{u})+dT(\vec{v})[/latex].

3. If a transformation satisfies [latex]T(c\vec{u}+d\vec{v}) = cT(\vec{u})+dT(\vec{v})[/latex] for all [latex]\vec{u},\vec{v}[/latex] in the domain of [latex]T[/latex] then it must be linear.

Theorem: If [latex]T[/latex] is a linear transformation then [latex]T(c_{1}{v}_1 + \cdots + c_{p}\vec{v}_p) = c_{1}T(\vec{v}_1) + \cdots + c_{p}T(\vec{v}_p)[/latex] for [latex]\vec{v}_{1}, \cdots, \vec{v}_{p}[/latex] in the domain of [latex]T[/latex]. We call this equality superposition principle.

Example 1: Let [latex]T: \mathbb{R}^2 \rightarrow \mathbb{R}^2[/latex] be a linear transformation that maps [latex]\vec{u} = \begin{bmatrix}1\\2\end{bmatrix}[/latex] into [latex]\begin{bmatrix}3\\4\end{bmatrix}[/latex] and maps [latex]\vec{v} = \begin{bmatrix}-1\\3\end{bmatrix}[/latex] into [latex]\begin{bmatrix}2\\-1\end{bmatrix}[/latex]. Use the fact that [latex]T[/latex] is linear to find the images under [latex]T[/latex] of [latex]2\vec{u},-3\vec{v}[/latex] and [latex]2\vec{u}-3\vec{v}[/latex].

Exercise 1: Let [latex]T: \mathbb{R}^3 \rightarrow \mathbb{R}^3[/latex] be a linear transformation that maps [latex]\vec{u} = \begin{bmatrix}1\\2\\-1\end{bmatrix}[/latex] into [latex]\begin{bmatrix}3\\5\\4\end{bmatrix}[/latex] and maps [latex]\vec{v} = \begin{bmatrix}-1\\4\\3\end{bmatrix}[/latex] into [latex]\begin{bmatrix}1\\-1\\-2\end{bmatrix}[/latex]. Use the fact that [latex]T[/latex] is linear to find the images under [latex]T[/latex] of [latex]-(1/2)\vec{u},2\vec{v}[/latex] and [latex]-(1/2)\vec{u}+2\vec{v}[/latex].

Fact: A matrix transformations is a linear transformation.

Definition: The standard basis of [latex]\mathbb{R}^n[/latex] is the columns set of [latex]I_n, {\vec{e_1}, \cdots, \vec{e_n}}[/latex].

Fact: Every vector [latex]\vec{x} = \begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}[/latex] is a linear combination of the [latex]\vec{e_i}[/latex]‘s and [latex]\vec{x} = x_{1}\vec{e_1} + x_{2}\vec{e_2} + \cdots + x_{n}\vec{e_n}[/latex].

Example 2: Let [latex]\vec{e_1} = \begin{bmatrix}1\\0\end{bmatrix}, \vec{e_2} = \begin{bmatrix}0\\1\end{bmatrix}, \vec{y_1} = \begin{bmatrix}2\\-1\end{bmatrix}[/latex] and [latex]\vec{y_2} = \begin{bmatrix}1\\-1\end{bmatrix}[/latex], and let [latex]T: \mathbb{R}^2 \rightarrow \mathbb{R}^2[/latex] a linear transformation map [latex]\vec{e_1}[/latex] to [latex]\vec{y_1}[/latex] and [latex]\vec{e_2}[/latex] to [latex]\vec{y_2}[/latex]. Find the image of [latex]\vec{u} = \begin{bmatrix}-3\\4\end{bmatrix}[/latex] and [latex]\vec{x} = \begin{bmatrix}x_1\\x_2\end{bmatrix}[/latex] under [latex]T[/latex].

Exercise 2: Let [latex]\vec{e_1} = \begin{bmatrix}1\\0\end{bmatrix}, \vec{e_2} = \begin{bmatrix}0\\1\end{bmatrix}, \vec{y_1} = \begin{bmatrix}-2\\3\end{bmatrix}[/latex] and [latex]\vec{y_2} = \begin{bmatrix}4\\-1\end{bmatrix}[/latex], and let [latex]T: \mathbb{R}^2 \rightarrow \mathbb{R}^2[/latex] a linear transformation map [latex]\vec{e_1}[/latex] to [latex]\vec{y_1}[/latex] and [latex]\vec{e_2}[/latex] to [latex]\vec{y_2}[/latex]. Find the image of [latex]\vec{u} = \begin{bmatrix}6\\-5\end{bmatrix}[/latex] and [latex]\vec{x} = \begin{bmatrix}x_1\\x_2\end{bmatrix}[/latex] under [latex]T[/latex].

Theorem: Let [latex]T: \mathbb{R}^n \rightarrow \mathbb{R}^m[/latex] be a linear transformation. Then there exists a unique [latex]m \times n[/latex] matrix such that [latex]T(\vec{x}) = A\vec{x}[/latex] for all vectors [latex]\vec{x}[/latex] in [latex]\mathbb{R}^n[/latex].

In fact, [latex]A = \begin{bmatrix}T(\vec{e_1}\cdots\vec{e_n})\end{bmatrix}[/latex] where [latex]\vec{e_i}[/latex] is the i-th column of the [latex]n \times n[/latex] identity matrix. [latex]A[/latex] is called the standard matrix of [latex]T[/latex].

Proof: For any vector [latex]\vec{x} = \begin{bmatrix}x_1\\\vdots\\x_n\end{bmatrix}[/latex], we can write [latex]\vec{x} = x_{1}\vec{e_{1}} + \cdots + x_{n}\vec{e_{n}}[/latex] then by the fact that [latex]T[/latex] is a linear transformation, we have [latex]T(\vec{x}) = x_{1}T(\vec{e_1}) + \cdots + x_{n}T(\vec{e_n}) = A\vec{x}[/latex]. The uniqueness is proved in the groupwork.

Theorem: Let [latex]T: \mathbb{R}^n \rightarrow \mathbb{R}^m[/latex] be a transformation. [latex]T[/latex] is linear if and only if it is a matrix transformation.

Theorem: Let [latex]\mathbb{R}^k\overset{T}{\rightarrow}\mathbb{R}^n\overset{S}{\rightarrow}\mathbb{R}^m[/latex] be linear transformations, and let [latex]A[/latex] and [latex]B[/latex] be the standard matrices of [latex]S[/latex] and [latex]T[/latex] respectively. Then [latex]S \circ T[/latex] is linear with standard matrix [latex]AB[/latex].

Example 3: Let [latex]\mathbb{R}^k\overset{T}{\rightarrow}\mathbb{R}^n\overset{S}{\rightarrow}\mathbb{R}^m[/latex] be linear transformation, and let [latex]A=\begin{bmatrix}1 & 2\\0 & -1\\3 & 0\end{bmatrix}[/latex] and [latex]B=\begin{bmatrix}0 & -1 & 2 & 0\\1 & 2 & 0 & 1\end{bmatrix}[/latex] be the standard matrices of [latex]S[/latex] and [latex]T[/latex] respectively. Find the standard matrix of [latex]S \circ T[/latex].

Exercise 3: Let [latex]\mathbb{R}^k\overset{T}{\rightarrow}\mathbb{R}^n\overset{S}{\rightarrow}\mathbb{R}^m[/latex] be linear transformation, and let [latex]A=\begin{bmatrix}1 & 2 & 0\\0 & -1 & 1\end{bmatrix}[/latex] and [latex]B=\begin{bmatrix}0 & -1\\1 & 0\\1 & 2\end{bmatrix}[/latex] be the standard matrices of [latex]S[/latex] and [latex]T[/latex] respectively. Find the standard matrix of [latex]S \circ T[/latex].

Example 4: Let [latex]T: \mathbb{R}^2 \rightarrow \mathbb{R}^2[/latex] be a linear transformation map [latex]\begin{bmatrix}2\\1\end{bmatrix}[/latex] to [latex]\vec{y_{1}} = \begin{bmatrix}1\\-1\end{bmatrix}[/latex] and [latex]\begin{bmatrix}-1\\0\end{bmatrix}[/latex] to [latex]\vec{y_{2}} = \begin{bmatrix}2\\1\end{bmatrix}[/latex]. Find the image of [latex]\vec{u} = \begin{bmatrix}-3\\2\end{bmatrix}[/latex] under [latex]T[/latex].

Exercise 4: Let [latex]T: \mathbb{R}^2 \rightarrow \mathbb{R}^2[/latex] be a linear transformation map [latex]\begin{bmatrix}1\\3\end{bmatrix}[/latex] to [latex]\vec{y_{1}} = \begin{bmatrix}2\\-1\end{bmatrix}[/latex] and [latex]\begin{bmatrix}-0\\2\end{bmatrix}[/latex] to [latex]\vec{y_{2}} = \begin{bmatrix}0\\1\end{bmatrix}[/latex]. Find the image of [latex]\vec{u} = \begin{bmatrix}-3\\2\end{bmatrix}[/latex] under [latex]T[/latex].

Group Work 1: Mark each statement True or False. Justify each answer.

a. A linear transformation is a special type of function.

b. If [latex]A[/latex] is a [latex]3 \times 5[/latex] matrix and [latex]T[/latex] is a transformation defined by [latex]T(\vec{x}) = A\vec{x}[/latex] then the domain of [latex]T[/latex] is [latex]\mathbb{R}^5[/latex].

c. If [latex]A[/latex] is an [latex]m \times n[/latex] matrix, then the range of the transformation [latex]\vec{x} \rightarrow A\vec{x}[/latex] is [latex]\mathbb{R}^m[/latex].

d. Every linear transformation is a matrix transformation.

e. A transformation [latex]T[/latex] is linear if and only if [latex]T(c\vec{u} + d\vec{v}) = cT(\vec{u}) + dT(\vec{v})[/latex] for all scalars [latex]c, d[/latex] and [latex]\vec{u}, \vec{v}[/latex] in the domain of [latex]T[/latex].

Group Work 2: Show the transformation [latex]T[/latex] defined by [latex]T(x_{1}, x_{2}) = (x_{1}-3x_{2}, x_{1}-2, 3x_{1}-5x_{2})[/latex] is not linear.

Group Work 3: Show the transformation [latex]T[/latex] defined by [latex]T(x_{1}, x_{2}) = (x_{1}-3|x_{2}|, x_{1}-4x_{2})[/latex] is not linear.

Group Work 4: Show the transformation [latex]T[/latex] defined by [latex]T(x_{1}, x_{2}, x_{3}) = (x_{1}, 0, x_{3})[/latex] is linear.

Group Work 5: Mark each statement True or False. Justify each answer.

a. The range of the transformation [latex]\vec{x} \rightarrow A\vec{x}[/latex] is the set of all linear combinations of the columns of [latex]A[/latex].

b. Every matrix transformation is a linear transformation.

c. A linear transformation preserves the operations of vector addition and
scalar multiplication.

d. A linear transformation, [latex]T: \mathbb{R}^n \rightarrow \mathbb{R}^m[/latex] always map the origin of [latex]\mathbb{R}^n[/latex] to the origin of [latex]\mathbb{R}^m[/latex].

e. Let [latex]T[/latex] and [latex]S[/latex] be linear transformations then [latex]T \circ S = S \circ T[/latex].

2.6B

Example 1: Let [latex]T: \mathbb{R}^2 \rightarrow \mathbb{R}^2[/latex] be the transformation that rotates each point in [latex]\mathbb{R}^2[/latex] about the origin through an angle [latex]\varphi[/latex], with counterclockwise rotation for a positive angle. This transformation is a linear transformation. Find the matrix [latex]A[/latex] such that [latex]T(\vec{x}) = A\vec{x}[/latex].

Exercise 1: Let [latex]T: \mathbb{R}^2 \rightarrow \mathbb{R}^2[/latex] be the transformation that rotates each point in [latex]\mathbb{R}^2[/latex] about the origin through an angle [latex]\varphi[/latex], with clockwise rotation for a positive angle. This transformation is a linear transformation. Find the matrix [latex]A[/latex] such that [latex]T(\vec{x}) = A\vec{x}[/latex].

Example 2: Find the standard matrix of a linear transformation [latex]T: \mathbb{R}^2 \rightarrow \mathbb{R}^2[/latex] that first reflects points through the horizontal [latex]x_{1}[/latex]-axis and then rotates points [latex]-\frac{\pi}{2}[/latex].

Exercise 2: Find the standard matrix of a linear transformation [latex]T: \mathbb{R}^2 \rightarrow \mathbb{R}^2[/latex] that first reflects points through the horizontal [latex]x_{1}[/latex]-axis and then reflects points through the line [latex]x_{1}=x_{2}[/latex].

Definition: 1. A map [latex]T: \mathbb{R}^n \rightarrow \mathbb{R}^m[/latex] is called onto if for all [latex]\vec{b}[/latex] in [latex]\mathbb{R}^m[/latex] there is at least one
[latex]\vec{x}[/latex] in [latex]\mathbb{R}^n[/latex] such that [latex]T(\vec{x}) = \vec{b}[/latex].

2. A map [latex]T: \mathbb{R}^n \rightarrow \mathbb{R}^m[/latex] is called one to one if [latex]T(\vec{x}) = T(\vec{y})[/latex] then [latex]\vec{x} = \vec{y}[/latex] for all [latex]\vec{x}, \vec{y}[/latex] in [latex]\mathbb{R}^n[/latex].

Example 3: Is the map defined by the matrix [latex]A = \begin{bmatrix}2 & -2 & 3 & 1\\0 & 3 & 2 & 2\\0 & 0 & 0 & 4\end{bmatrix}[/latex] one to one linear transformation?

Exercise 3: Is the map defined by the matrix [latex]A = \begin{bmatrix}2 & -2 & -5 & 1\\0 & 3 & 4 & 1\\0 & 0 & 1 & 2\\0 & 0 & 0 & 0\end{bmatrix}[/latex] one to one linear transformation?

Theorem: Let [latex]\mathbb{R}^n\rightarrow\mathbb{R}^m[/latex] be a linear transformations. [latex]T[/latex] is one to one if and only if [latex]T(\vec{x}) = \vec{0}[/latex] only has the trivial solution.

Theorem: Let [latex]\mathbb{R}^n\rightarrow\mathbb{R}^m[/latex] with standard matrix [latex]A[/latex]. Then

(1) [latex]T[/latex] is onto if and only if [latex]A[/latex] has pivot positions in every row.

(2) [latex]T[/latex] is one to one if and only if [latex]A[/latex] has pivot position in every column.

Example 4: Let [latex]T(x_{1}, x_{2}) = (x_{1} - x_{2}, 2x_{1} + 3x_{2}, 3x_{1} - 2x_{2})[/latex]. Show that [latex]T[/latex] is a one to one linear transformation. Is [latex]T[/latex] a onto transformation?

Example 4: Let [latex]T(x_{1}, x_{2}) = (-x_{1} + x_{2}, 2x_{1} - x_{2}, -3x_{1} + 2x_{2})[/latex]. Show that [latex]T[/latex] is a one to one linear transformation. Is [latex]T[/latex] a onto transformation?

GroupWork 1: Mark each statement True or False. Justify each answer.

a. A linear transformation is completely determined by its effect on the
columns of the [latex]n \times n[/latex] matrix.

b. If [latex]T: \mathbb{R}^2 \rightarrow \mathbb{R}^2[/latex] rotates vectors about the origin through an angle [latex]\varphi[/latex], then [latex]T[/latex] is a linear transformation.

c. When two linear transformations are performed one after another, the
combined effect may not always be a linear transformation.

d. A map [latex]T: \mathbb{R}^n \rightarrow \mathbb{R}^m[/latex] is onto if every [latex]\vec{x}[/latex] in [latex]\mathbb{R}^n[/latex] maps onto some vector in [latex]\mathbb{R}^m[/latex].

e. If the standard matrix of a linear transformation is a [latex]3 \times 2[/latex] matrix then [latex]T[/latex] cannot be one to one.

Group Work 2: Let [latex]T: \mathbb{R}^n \rightarrow \mathbb{R}^m[/latex] and [latex]S: \mathbb{R}^m \rightarrow \mathbb{R}^n[/latex] be two linear transformations. Show the transformation from [latex]\mathbb{R}^n[/latex] to [latex]\mathbb{R}^p[/latex] defined by sending [latex]\vec{x}[/latex] in [latex]\mathbb{R}^n[/latex] to [latex]S(T(\vec{x}))[/latex] in [latex]\mathbb{R}^p[/latex] is a linear transformation.

Group Work 3: Mark each statement True or False. Justify each answer.

a. If the standard matrix of a linear transformation is [latex]4 \times 3[/latex] then the map is onto.

b. Every linear transformation from [latex]\mathbb{R}^n[/latex] to [latex]\mathbb{R}^m[/latex] is a matrix transformation.

c. The columns of the standard matrix of a linear transformation [latex]T[/latex] from [latex]\mathbb{R}^n[/latex] to [latex]\mathbb{R}^m[/latex] is the images of the the columns of the [latex]n \times n[/latex] identity matrix under
[latex]T[/latex].

d. A linear transformation, [latex]T: \mathbb{R}^n \rightarrow \mathbb{R}^m[/latex] is one to one if each vector in [latex]\mathbb{R}^n[/latex] maps to a unique vector in [latex]\mathbb{R}^m[/latex].

Group Work 4: A primitive society has three basic needs: food, shelter, and clothing. There are thus three industries in the society—the farming, housing, and garment industries—that produce these commodities. Each of these industries consumes a certain proportion of the total output of each commodity according to the following table.

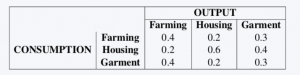
Find the annual prices that each industry must charge for its income to equal its expenditures.