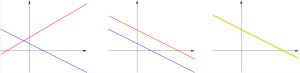
Section 1.1 Linear Equations

Definition: 1. A linear equation in the variables, [latex]x_{1},...,x_{n}[/latex] is an equation that can be written in the form [latex]a_{1}x_{1}+....+a_{n}x_{n}=b[/latex] where [latex]a_{1},...,a_{n},b[/latex] are constants, real numbers or complex numbers.

2. A system of linear equations (or a linear system) is a collection of one or more linear equations involving the same variables, [latex]x_{1},....,x_{n}[/latex].

3. A solution of the system is a list of numbers, [latex]s_{1},...,s_{n}[/latex], that makes each equation a true statement when the values [latex]s_{1},...,s_{n}[/latex] are substituted for [latex]x_{1},...,x_{n}[/latex] respectively.

4. Solve a system means “find all solutions to the system.” The set of all possible solutions is called the solution set of the linear system.

5. Two linear systems are called equivalent if they have the same solution set.

Theorem(fact): A system of linear equations has no solution, or exactly one solution, or infinitely many solutions.

Definition: A system of linear equations is said to be consistent if it has either one solution or infinitely many solutions. A system of linear equations is said to be inconsistent if it has no solution.

Definition: 1. The essential information of a linear system can be recorded compactly in a rectangular array called a matrix.

2. The matrix associated to a linear system is called the coefficient matrix of the linear system.

3. An augmented matrix of a system consists of the coefficient matrix with an added column containing the constants from the right sides of the equations.

Exercise 1: Write down the coefficient matrix and the augmented matrix of the linear system.

[latex]\begin{array}{ccc} 2x_{2}-3x_{3}+x_{4} & = & 1\\ 3x_{1}-x_{3}+4x_{4} & = & 2\\ x_{1}+x_{2} & = & 3\\ x_{2}-x_{3}+x_{4} & = & 1 \end{array}[/latex]

Definition: The size of a matrix tells how many rows and columns it has. If [latex]m[/latex] and [latex]n[/latex] are positive numbers, an [latex]m\times n[/latex] matrix is a rectangular array of numbers with [latex]m[/latex] rows and [latex]n[/latex] columns.(The number of rows always comes first.)

Definition: 1. Elementary row operations include the following:

A. (Replacement) Replace one row by the sum of itself and a multiple of another row.

B. (Interchange) Interchange two rows.

C. (Scaling) Multiply all entries in a row by a nonzero constant.

2. Two matrices are called row equivalent if there is a sequence of elementary row operations that transforms one matrix into the other.

Facts: 1. Row operations are reversible.

2. If the augmented matrices of two linear systems are row equivalent, then the two systems are equivalent, i.e. they have the same solution set.

Questions: Given a linear system 1. Is the system consistent? 2. If the system has a solution, is the solution unique?

Example 2: Determine if the following system is consistent.

[latex]\begin{array}{ccc} x_{2}-x_{3} & = & 4\\ 3x_{1}+x_{3} & = & 1\\ 2x_{1}-x_{2} & = & 2 \end{array}[/latex]

Exercise 2: Determine if the following system is consistent.

[latex]\begin{array}{ccc} 2x_{2}-3x_{3} & = & 1\\ 3x_{1}-x_{3} & = & 2\\ x_{1}+x_{2} & = & 3 \end{array}[/latex]

Example 3: Determine if the following system is consistent.

[latex]\begin{array}{ccc} x_{1}+x_{2}-3x_{3} & = & 4\\ x_{1}-2x_{3} & = & 1\\ -x_{2}+x_{3} & = & 2 \end{array}[/latex]

Exercise 3: Determine if the following system is consistent.

[latex]\begin{array}{ccc} -x_{1}+x_{2}-3x_{3} & = & 1\\ x_{2}+3x_{3} & = & 2\\ x_{1}-2x_{2} & = & 3 \end{array}[/latex]

Group Work 1: Do the following three lines have a common point of intersection?

[latex]\begin{array}{cc} 2x_{1}-x_{2} & =1\\ x_{1}+x_{2} & =2\\ -x_{1}+3x_{2} & =3 \end{array}[/latex]

Group Work 2: Do the following three planes have a common point of intersection?

[latex]\begin{array}{cc} 2x_{1}-x_{2}+x_{3} & =1\\ x_{1}+x_{2} & =2\\ x_{2}+3x_{3} & =3 \end{array}[/latex]

Group Work 3: Find a [latex]h[/latex] such that the matrix is the augmented matrix of a consistent linear system.

[latex]\left[\begin{array}{ccc} 2 & -3 & 4\\ -4 & h & 1 \end{array}\right][/latex]

Group Work 4: Find a [latex]h[/latex] such that the matrix is the augmented matrix of an inconsistent linear system.

[latex]\left[\begin{array}{ccc} 1 & 2 & 3\\ 4 & h & 1 \end{array}\right][/latex]