Section 2.6 Linear Transformations

2.6A

Definition: A transformation (or mapping) $T$ is linear if

(1) $T(\overrightarrow{u}+\overrightarrow{v})=T(\overrightarrow{u})+T(\overrightarrow{v})$ for all $\overrightarrow{u},\overrightarrow{v}$ in the domain of $T$.

(2) $T(c\overrightarrow{u})=cT(\overrightarrow{u})$ for all scalars $c$ and all $\overrightarrow{u}$ in the domain of $T$.

Fact: 1. Linear transformations preserve the operations of vector addition and scalar multiplication.

2. If $T$ is a linear transformation, then $T(\overrightarrow{0})=\overrightarrow{0}$ and $T(c\overrightarrow{u}+d\overrightarrow{v})=cT(\overrightarrow{u})+dT(\overrightarrow{v})$.

3. If a transformation satisfies $T(c\overrightarrow{u}+d\overrightarrow{v})=cT(\overrightarrow{u})+dT(\overrightarrow{v})$ for all $\overrightarrow{u},\overrightarrow{v}$ in the domain of $T$ then it must be linear.

Theorem: If $T$ is a linear transformation then $T(c_1{v}_1+\cdots +c_p{\overrightarrow{v}}_p)=c_{1}T({\overrightarrow{v}}_1)+\cdots +c_{p}T({\overrightarrow{v}}_p)$ for ${\overrightarrow{v}}_1,\cdots ,{\overrightarrow{v}}_p$ in the domain of $T$. We call this equality superposition principle.

Example 1: Let $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be a linear transformation that maps $\overrightarrow{u}=\left[\begin{array}{c}1\\ 2\end{array}\right]$ into $\left[\begin{array}{c}3\\ 4\end{array}\right]$ and maps $\overrightarrow{v}=\left[\begin{array}{c}-1\\ 3\end{array}\right]$ into $\left[\begin{array}{c}2\\ -1\end{array}\right]$. Use the fact that $T$ is linear to find the images under $T$ of $2\overrightarrow{u},-3\overrightarrow{v}$ and $2\overrightarrow{u}-3\overrightarrow{v}$.

Exercise 1: Let $T:{\mathbb{R}}^3\to {\mathbb{R}}^3$ be a linear transformation that maps $\overrightarrow{u}=\left[\begin{array}{c}1\\ 2\\ -1\end{array}\right]$ into $\left[\begin{array}{c}3\\ 5\\ 4\end{array}\right]$ and maps $\overrightarrow{v}=\left[\begin{array}{c}-1\\ 4\\ 3\end{array}\right]$ into $\left[\begin{array}{c}1\\ -1\\ -2\end{array}\right]$. Use the fact that $T$ is linear to find the images under $T$ of $-(1/2)\overrightarrow{u},2\overrightarrow{v}$ and $-(1/2)\overrightarrow{u}+2\overrightarrow{v}$.

Fact: A matrix transformations is a linear transformation.

Definition: The standard basis of ${\mathbb{R}}^n$ is the columns set of $I_n,\overrightarrow{e_1},\cdots ,\overrightarrow{e_n}$.

Fact: Every vector $\overrightarrow{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]$ is a linear combination of the $\overrightarrow{e_i}$‘s and $\overrightarrow{x}=x_1\overrightarrow{e_1}+x_2\overrightarrow{e_2}+\cdots +x_n\overrightarrow{e_n}$.

Example 2: Let $\overrightarrow{e_1}=\left[\begin{array}{c}1\\ 0\end{array}\right],\overrightarrow{e_2}=\left[\begin{array}{c}0\\ 1\end{array}\right],\overrightarrow{y_1}=\left[\begin{array}{c}2\\ -1\end{array}\right]$ and $\overrightarrow{y_2}=\left[\begin{array}{c}1\\ -1\end{array}\right]$, and let $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ a linear transformation map $\overrightarrow{e_1}$ to $\overrightarrow{y_1}$ and $\overrightarrow{e_2}$ to $\overrightarrow{y_2}$. Find the image of $\overrightarrow{u}=\left[\begin{array}{c}-3\\ 4\end{array}\right]$ and $\overrightarrow{x}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$ under $T$.

Exercise 2: Let $\overrightarrow{e_1}=\left[\begin{array}{c}1\\ 0\end{array}\right],\overrightarrow{e_2}=\left[\begin{array}{c}0\\ 1\end{array}\right],\overrightarrow{y_1}=\left[\begin{array}{c}-2\\ 3\end{array}\right]$ and $\overrightarrow{y_2}=\left[\begin{array}{c}4\\ -1\end{array}\right]$, and let $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ a linear transformation map $\overrightarrow{e_1}$ to $\overrightarrow{y_1}$ and $\overrightarrow{e_2}$ to $\overrightarrow{y_2}$. Find the image of $\overrightarrow{u}=\left[\begin{array}{c}6\\ -5\end{array}\right]$ and $\overrightarrow{x}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$ under $T$.

Theorem: Let $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a linear transformation. Then there exists a unique $m\times n$ matrix such that $T(\overrightarrow{x})=A\overrightarrow{x}$ for all vectors $\overrightarrow{x}$ in ${\mathbb{R}}^n$.

In fact, $A=\left[\begin{array}{c}T(\overrightarrow{e_1}\cdots \overrightarrow{e_n})\end{array}\right]$ where $\overrightarrow{e_i}$ is the i-th column of the $n\times n$ identity matrix. $A$ is called the standard matrix of $T$.

Proof: For any vector $\overrightarrow{x}=\left[\begin{array}{c}{x}_1\\ ⋮\\ x_n\end{array}\right]$, we can write $\overrightarrow{x}=x_1\overrightarrow{e_1}+\cdots +x_n\overrightarrow{e_n}$ then by the fact that $T$ is a linear transformation, we have $T(\overrightarrow{x})=x_{1}T(\overrightarrow{e_1})+\cdots +x_{n}T(\overrightarrow{e_n})=A\overrightarrow{x}$. The uniqueness is proved in the groupwork.

Theorem: Let $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ be a transformation. $T$ is linear if and only if it is a matrix transformation.

Theorem: Let ${\mathbb{R}}^k\stackrel{T}{\to }{\mathbb{R}}^n\stackrel{S}{\to }{\mathbb{R}}^m$ be linear transformations, and let $A$ and $B$ be the standard matrices of $S$ and $T$ respectively. Then $S\circ T$ is linear with standard matrix $AB$.

Example 3: Let ${\mathbb{R}}^k\stackrel{T}{\to }{\mathbb{R}}^n\stackrel{S}{\to }{\mathbb{R}}^m$ be linear transformation, and let $A=\left[\begin{array}{cc}1& 2\\ 0& -1\\ 3& 0\end{array}\right]$ and $B=\left[\begin{array}{cccc}0& -1& 2& 0\\ 1& 2& 0& 1\end{array}\right]$ be the standard matrices of $S$ and $T$ respectively. Find the standard matrix of $S\circ T$.

Exercise 3: Let ${\mathbb{R}}^k\stackrel{T}{\to }{\mathbb{R}}^n\stackrel{S}{\to }{\mathbb{R}}^m$ be linear transformation, and let $A=\left[\begin{array}{ccc}1& 2& 0\\ 0& -1& 1\end{array}\right]$ and $B=\left[\begin{array}{cc}0& -1\\ 1& 0\\ 1& 2\end{array}\right]$ be the standard matrices of $S$ and $T$ respectively. Find the standard matrix of $S\circ T$.

Example 4: Let $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be a linear transformation map $\left[\begin{array}{c}2\\ 1\end{array}\right]$ to $\overrightarrow{y_1}=\left[\begin{array}{c}1\\ -1\end{array}\right]$ and $\left[\begin{array}{c}-1\\ 0\end{array}\right]$ to $\overrightarrow{y_2}=\left[\begin{array}{c}2\\ 1\end{array}\right]$. Find the image of $\overrightarrow{u}=\left[\begin{array}{c}-3\\ 2\end{array}\right]$ under $T$.

Exercise 4: Let $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be a linear transformation map $\left[\begin{array}{c}1\\ 3\end{array}\right]$ to $\overrightarrow{y_1}=\left[\begin{array}{c}2\\ -1\end{array}\right]$ and $\left[\begin{array}{c}-0\\ 2\end{array}\right]$ to $\overrightarrow{y_2}=\left[\begin{array}{c}0\\ 1\end{array}\right]$. Find the image of $\overrightarrow{u}=\left[\begin{array}{c}-3\\ 2\end{array}\right]$ under $T$.

Group Work 1: Mark each statement True or False. Justify each answer.

a. A linear transformation is a special type of function.

b. If $A$ is a $3\times 5$ matrix and $T$ is a transformation defined by $T(\overrightarrow{x})=A\overrightarrow{x}$ then the domain of $T$ is ${\mathbb{R}}^5$.

c. If $A$ is an $m\times n$ matrix, then the range of the transformation $\overrightarrow{x}\to A\overrightarrow{x}$ is ${\mathbb{R}}^m$.

d. Every linear transformation is a matrix transformation.

e. A transformation $T$ is linear if and only if $T(c\overrightarrow{u}+d\overrightarrow{v})=cT(\overrightarrow{u})+dT(\overrightarrow{v})$ for all scalars $c,d$ and $\overrightarrow{u},\overrightarrow{v}$ in the domain of $T$.

Group Work 2: Show the transformation $T$ defined by $T(x_1,x_2)=(x_1-3x_2,x_1-2,3x_1-5x_2)$ is not linear.

Group Work 3: Show the transformation $T$ defined by $T(x_1,x_2)=(x_1-3|x_2|,x_1-4x_2)$ is not linear.

Group Work 4: Show the transformation $T$ defined by $T(x_1,x_2,x_3)=(x_1,0,x_3)$ is linear.

Group Work 5: Mark each statement True or False. Justify each answer.

a. The range of the transformation $\overrightarrow{x}\to A\overrightarrow{x}$ is the set of all linear combinations of the columns of $A$.

b. Every matrix transformation is a linear transformation.

c. A linear transformation preserves the operations of vector addition and
scalar multiplication.

d. A linear transformation, $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ always map the origin of ${\mathbb{R}}^n$ to the origin of ${\mathbb{R}}^m$.

e. Let $T$ and $S$ be linear transformations then $T\circ S=S\circ T$.

2.6B

Example 1: Let $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be the transformation that rotates each point in ${\mathbb{R}}^2$ about the origin through an angle $\phi$, with counterclockwise rotation for a positive angle. This transformation is a linear transformation. Find the matrix $A$ such that $T(\overrightarrow{x})=A\overrightarrow{x}$.

Exercise 1: Let $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be the transformation that rotates each point in ${\mathbb{R}}^2$ about the origin through an angle $\phi$, with clockwise rotation for a positive angle. This transformation is a linear transformation. Find the matrix $A$ such that $T(\overrightarrow{x})=A\overrightarrow{x}$.

Example 2: Find the standard matrix of a linear transformation $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ that first reflects points through the horizontal $x_1$-axis and then rotates points $-\frac{\pi }{2}$.

Exercise 2: Find the standard matrix of a linear transformation $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ that first reflects points through the horizontal $x_1$-axis and then reflects points through the line $x_1=x_2$.

Definition: 1. A map $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ is called onto if for all $\overrightarrow{b}$ in ${\mathbb{R}}^m$ there is at least one
$\overrightarrow{x}$ in ${\mathbb{R}}^n$ such that $T(\overrightarrow{x})=\overrightarrow{b}$.

2. A map $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ is called one to one if $T(\overrightarrow{x})=T(\overrightarrow{y})$ then $\overrightarrow{x}=\overrightarrow{y}$ for all $\overrightarrow{x},\overrightarrow{y}$ in ${\mathbb{R}}^n$.

Example 3: Is the map defined by the matrix $A=\left[\begin{array}{cccc}2& -2& 3& 1\\ 0& 3& 2& 2\\ 0& 0& 0& 4\end{array}\right]$ one to one linear transformation?

Exercise 3: Is the map defined by the matrix $A=\left[\begin{array}{cccc}2& -2& -5& 1\\ 0& 3& 4& 1\\ 0& 0& 1& 2\\ 0& 0& 0& 0\end{array}\right]$ one to one linear transformation?

Theorem: Let ${\mathbb{R}}^n\to {\mathbb{R}}^m$ be a linear transformations. $T$ is one to one if and only if $T(\overrightarrow{x})=\overrightarrow{0}$ only has the trivial solution.

Theorem: Let ${\mathbb{R}}^n\to {\mathbb{R}}^m$ with standard matrix $A$. Then

(1) $T$ is onto if and only if $A$ has pivot positions in every row.

(2) $T$ is one to one if and only if $A$ has pivot position in every column.

Example 4: Let $T(x_1,x_2)=(x_1-x_2,2x_1+3x_2,3x_1-2x_2)$. Show that $T$ is a one to one linear transformation. Is $T$ a onto transformation?

Example 4: Let $T(x_1,x_2)=(-x_1+x_2,2x_1-x_2,-3x_1+2x_2)$. Show that $T$ is a one to one linear transformation. Is $T$ a onto transformation?

GroupWork 1: Mark each statement True or False. Justify each answer.

a. A linear transformation is completely determined by its effect on the
columns of the $n\times n$ matrix.

b. If $T:{\mathbb{R}}^2\to {\mathbb{R}}^2$ rotates vectors about the origin through an angle $\phi$, then $T$ is a linear transformation.

c. When two linear transformations are performed one after another, the
combined effect may not always be a linear transformation.

d. A map $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ is onto if every $\overrightarrow{x}$ in ${\mathbb{R}}^n$ maps onto some vector in ${\mathbb{R}}^m$.

e. If the standard matrix of a linear transformation is a $3\times 2$ matrix then $T$ cannot be one to one.

Group Work 2: Let $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ and $S:{\mathbb{R}}^m\to {\mathbb{R}}^n$ be two linear transformations. Show the transformation from ${\mathbb{R}}^n$ to ${\mathbb{R}}^p$ defined by sending $\overrightarrow{x}$ in ${\mathbb{R}}^n$ to $S(T(\overrightarrow{x}))$ in ${\mathbb{R}}^p$ is a linear transformation.

Group Work 3: Mark each statement True or False. Justify each answer.

a. If the standard matrix of a linear transformation is $4\times 3$ then the map is onto.

b. Every linear transformation from ${\mathbb{R}}^n$ to ${\mathbb{R}}^m$ is a matrix transformation.

c. The columns of the standard matrix of a linear transformation $T$ from ${\mathbb{R}}^n$ to ${\mathbb{R}}^m$ is the images of the the columns of the $n\times n$ identity matrix under
$T$.

d. A linear transformation, $T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ is one to one if each vector in ${\mathbb{R}}^n$ maps to a unique vector in ${\mathbb{R}}^m$.

Group Work 4: A primitive society has three basic needs: food, shelter, and clothing. There are thus three industries in the society—the farming, housing, and garment industries—that produce these commodities. Each of these industries consumes a certain proportion of the total output of each commodity according to the following table.

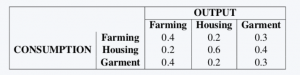
Find the annual prices that each industry must charge for its income to equal its expenditures.