Section 4.1 Subspaces and Spanning
Definition: A subspace of [latex]\mathbb{R}^n[/latex] is any set H in [latex]\mathbb{R}^n[/latex] that has three properties:
a) The zero vector is in H.
b) For each [latex]\vec{u}[/latex] and [latex]\vec{v}[/latex] in H, the sum [latex]\vec{u} + \vec{v}[/latex] is in H
c) For each [latex]\vec{u}[/latex] in H and each scalar [latex]c[/latex] in [latex]\mathbb{R}[/latex], the vector [latex]c\vec{u}[/latex] is in H.
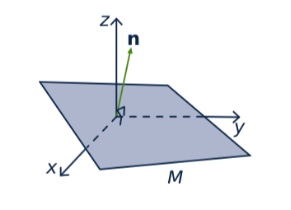
Fact: The subspace definition is geometric, a plane through the origin is a subspace of [latex]\mathbb{R}^3[/latex].
Example 1: Let [latex]H = \begin{Bmatrix}\begin{bmatrix}x\\y\end{bmatrix}: x \geq 0, y \geq 0\end{Bmatrix}[/latex] the first quadrant in the [latex]xy[/latex]-plane. Show (a): if [latex]\vec{u}[/latex] and [latex]\vec{v}[/latex] are in H then [latex]\vec{u} + \vec{v}[/latex] are in H, (b): Find a vector [latex]\vec{u}[/latex] and a scalar [latex]c[/latex] such that [latex]c\vec{u}[/latex] is not in H ( this shows V is not a subspace of [latex]\mathbb{R}^2[/latex]).
Exercise 1: Let [latex]H = \begin{Bmatrix}\begin{bmatrix}x\\y\end{bmatrix}: x \geq 0, y \geq 0\end{Bmatrix}[/latex] the union of first quadrant and the third quadrant in the [latex]xy[/latex]-plane. Show (a): if [latex]\vec{u}[/latex] in H and any scalar [latex]c[/latex], then [latex]c\vec{u}[/latex]is in H, (b): Find vectors [latex]\vec{u}[/latex] and [latex]\vec{v}[/latex] in H such that [latex]\vec{u} + \vec{v}[/latex] is not in H.
Fact: 1. The set only has zero vector, [latex]\vec{0}[/latex] is a subspace of [latex]\mathbb{R}^n[/latex] and we call it zero subspace which is written as [latex]\begin{Bmatrix}\vec{0}\end{Bmatrix}[/latex].
2. [latex]\mathbb{R}^2[/latex] is NOT a subspace of [latex]\mathbb{R}^3[/latex] but [latex]H = \begin{Bmatrix}\begin{bmatrix}a\\b\\0\end{bmatrix}: a, b & \text{in} & \mathbb{R}^n\end{Bmatrix}[/latex] is a subspace of [latex]\mathbb{R}^3[/latex].
Theorem: If [latex]\vec{x_{1}}, \cdots, \vec{x_{p}}[/latex] are vectors in [latex]\mathbb{R}^n[/latex], then Span[latex]\begin{Bmatrix}\vec{x_{1}}, \cdots, \vec{x_{p}}\end{Bmatrix}[/latex] is a subspace of [latex]\mathbb{R}^n[/latex].
Example 2: Let H be the set of all vectors of the form [latex](2a + 3b, -a + 2b, 2a, -b)[/latex] in [latex]\mathbb{R}^4[/latex] where [latex]a, b[/latex] are in [latex]\mathbb{R}[/latex]. Show H is a subspace of [latex]\mathbb{R}^4[/latex].
Exercise 2: Let H be the set of all vectors of the form [latex](s + 4t, -s + t, 2s + t, s - 2t)[/latex] in [latex]\mathbb{R}^4[/latex] where [latex]s, t[/latex] are in [latex]\mathbb{R}[/latex]. Show H is a subspace of [latex]\mathbb{R}^4[/latex].
Example 3: Let W be the set of all vectors of the form shown where [latex]a,b,c[/latex] are scalars. Either find a set of vectors that spans W or show W is not a subspace. (a) [latex]\begin{bmatrix}2a + b\\-3a + b\\2\end{bmatrix}[/latex] (b) [latex]\begin{bmatrix}-a + b - c\\2a + b\\4c\\3b + c\end{bmatrix}[/latex].
Exercise 3: Let W be the set of all vectors of the form shown where [latex]a,b,c[/latex] are scalars. Either find a set of vectors that spans W or show W is not a subspace. (a) [latex]\begin{bmatrix}1\\-a + b\\2a-b\end{bmatrix}[/latex] (b) [latex]\begin{bmatrix}-a + 2b - c\\a - b\\0\\3b + 3c\end{bmatrix}[/latex].
Definition: The column space of an [latex]m \times n[/latex] matrix [latex]A[/latex] is the set Col [latex]A[/latex] of all linear combinations of the columns of [latex]A[/latex]. The image space of an [latex]m \times n[/latex] matrix [latex]A[/latex], denote Im[latex]A[/latex], are defined by Im[latex]A = \begin{Bmatrix}A\vec{x}|\vec{x} & \text{in} & \mathbb{R}^n\end{Bmatrix}[/latex]. Im[latex]A =[/latex] Col [latex]A[/latex] is a subspace of [latex]\mathbb{R}^n[/latex].
Fact: 1. If [latex]A = \begin{bmatrix}\vec{a_{1}}\cdots\vec{a_{n}}\end{bmatrix}[/latex] with the columns in [latex]\mathbb{R}^m[/latex] then Col[latex]A[/latex] is the same as Span[latex]\begin{Bmatrix}\vec{a_{1}}, \cdots, \vec{a_{n}}\end{Bmatrix}[/latex] a subspace of [latex]\mathbb{R}^m[/latex].
2. The vector [latex]\vec{b}[/latex] is a linear combination of the columns of [latex]A[/latex] if and only if [latex]\vec{b}[/latex] can be written as [latex]A\vec{x}[/latex] for some [latex]\vec{x}[/latex], that is, if and only if the equation [latex]A\vec{x} = \vec{b}[/latex] has a solution if and only if [latex]A\vec{x} = \vec{b}[/latex] is consistent and [latex]\vec{b}[/latex] is in Col[latex]A[/latex].
Example 4: Show [latex]\begin{bmatrix}1\\2\\3\end{bmatrix}[/latex] is in the Col[latex]A[/latex] where [latex]A = \begin{bmatrix}1 & 2 & -1\\3 & 0 & 2\\0 & -1 & 2\end{bmatrix}[/latex].
Exercise 4: Show [latex]\begin{bmatrix}2\\1\\-1\end{bmatrix}[/latex] is in the Col[latex]A[/latex] where [latex]A = \begin{bmatrix}2 & 1 & 1\\1 & 0 & -2\\0 & -1 & 2\end{bmatrix}[/latex].
Example 5: Find the values [latex]h[/latex] such that [latex]\vec{y}[/latex] is in the subspace span by [latex]\vec{v_{1}},\vec{v_{2}},\vec{v_{3}}[/latex] where [latex]\vec{y} = \begin{bmatrix}1\\2\\h\end{bmatrix}, \vec{x_{1}} = \begin{bmatrix}-1\\0\\3\end{bmatrix}, \vec{x_{2}} = \begin{bmatrix}0\\2\\4\end{bmatrix}[/latex] and [latex]\vec{x_{3}} = \begin{bmatrix}-2\\4\\14\end{bmatrix}[/latex].
Exercise 5: Find the values [latex]h[/latex] such that [latex]\vec{y}[/latex] is in the subspace span by [latex]\vec{v_{1}},\vec{v_{2}},\vec{v_{3}}[/latex] where [latex]\vec{y} = \begin{bmatrix}1\\h\\3\end{bmatrix}, \vec{x_{1}} = \begin{bmatrix}0\\1\\3\end{bmatrix}, \vec{x_{2}} = \begin{bmatrix}3\\0\\4\end{bmatrix}[/latex] and [latex]\vec{x_{3}} = \begin{bmatrix}6\\-2\\2\end{bmatrix}[/latex].
Group Work 1: True or False. Justify each answer:
a. A subspace of [latex]\mathbb{R}^n[/latex] is any set [latex]H[/latex] such that (i) the zero vector is in [latex]H[/latex], (ii) [latex]\vec{u}, \vec{v}[/latex] and [latex]\vec{u} + \vec{v}[/latex] are in [latex]H[/latex] (iii) [latex]c[/latex] is a scalar, [latex]c\vec{u}[/latex] is in [latex]H[/latex].
b. If [latex]\vec{v_{1}}, \cdots, \vec{v_{p}}[/latex] are in [latex]\mathbb{R}^n[/latex], then span[latex]\begin{Bmatrix}\vec{v_{1}}, \cdots, \vec{v_{p}}\end{Bmatrix}[/latex] is the same as the column space of the matrix [latex]\begin{bmatrix}\vec{v_{1}}, \cdots, \vec{v_{p}}\end{bmatrix}[/latex].
c. The set of all solutions of a system of [latex]m[/latex] homogeneous equations in [latex]n[/latex] unknowns is a subspace of [latex]\mathbb{R}^m[/latex].
d. The null space of an [latex]m \times n[/latex] matrix is a subspace of [latex]\mathbb{R}^n[/latex].
e. The column space of a matrix [latex]A[/latex] is the set of solutions of [latex]A\vec{x} = \vec{b}[/latex].
Group Work 2: Construct a nonzero [latex]3 \times 3[/latex] matrix [latex]A[/latex] and a nonzero vector [latex]\vec{b}[/latex] such that [latex]\vec{b}[/latex] is in Col[latex]A[/latex], but [latex]\vec{b}[/latex] is not the same as any one of the columns of [latex]A[/latex].
Group Work 3: Suppose [latex]F[/latex] is a [latex]5 \times 5[/latex] matrix whose column space is not equal to [latex]\mathbb{R}^5[/latex]. What can you say about Nul[latex]F[/latex]?
Group Work 4: In each case either show that the statement is true or give an
example showing that it is false.
a. If [latex]U \neq \mathbb{R}^n[/latex] is a subspace of [latex]\mathbb{R}^n[/latex] and [latex]\vec{u} + \vec{v}[/latex] is in [latex]U[/latex] then [latex]\vec{u}[/latex] and [latex]\vec{v}[/latex] are both in [latex]U[/latex].
b. If [latex]U[/latex] is a subspace of [latex]\mathbb{R}^n[/latex] and [latex]r\vec{u}[/latex] is in [latex]U[/latex] for all [latex]r[/latex] in [latex]\mathbb{R}[/latex] then [latex]\vec{u}[/latex] is in [latex]U[/latex].
c. If [latex]U[/latex] is a subspace of [latex]\mathbb{R}^n[/latex] and [latex]\vec{u}[/latex] is in [latex]U[/latex] then [latex]-\vec{u}[/latex] is also in [latex]U[/latex].
d. If [latex]\vec{x}[/latex] is in [latex]U[/latex] and [latex]U =[/latex] span[latex]\begin{Bmatrix}\vec{y}, \vec{z}\end{Bmatrix}[/latex], then [latex]U =[/latex] span[latex]\begin{Bmatrix}\vec{x}, \vec{y}, \vec{z}\end{Bmatrix}[/latex].
e. The empty set of vectors in [latex]\mathbb{R}^n[/latex] is a subspace of [latex]\mathbb{R}^n[/latex].
f. [latex]\begin{bmatrix}0\\1\end{bmatrix}[/latex] is in span[latex]\begin{Bmatrix}\begin{bmatrix}1\\0\end{bmatrix}, \begin{bmatrix}2\\0\end{bmatrix}\end{Bmatrix}[/latex].
Group Work 5: Construct a nonzero [latex]3 \times 3[/latex] matrix [latex]A[/latex] and a vector [latex]\vec{b}[/latex] such that [latex]\vec{b}[/latex] is not in Col[latex]A[/latex].
Group Work 6: If [latex]A[/latex] is a [latex]5 \times 5[/latex] matrix and Nul[latex]A[/latex] is the zero subspace, what can you say about solutions of equations of the form [latex]A\vec{x} = \vec{b}[/latex] for [latex]\vec{b}[/latex] in [latex]\mathbb{R}^5[/latex]?
Group Work 7: What can you say about Nul[latex]B[/latex] when [latex]B[/latex] is a [latex]5 \times 4[/latex] matrix with linearly independent columns?

