Acid-Base Titrations (14.7)

 

As seen in the chapter on the stoichiometry of chemical reactions, titrations can be used to quantitatively analyze solutions for their acid or base concentrations. In this section, we will explore the underlying chemical equilibria that make acid-base titrimetry a useful analytical technique.

Titration Curves

A titration curve is a plot of some solution property versus the amount of added titrant. For acid-base titrations, solution pH is a useful property to monitor because it varies predictably with the solution composition and, therefore, may be used to monitor the titration’s progress and detect its end point. The following example exercise demonstrates the computation of pH for a titration solution after additions of several specified titrant volumes. The first example involves a strong acid titration that requires only stoichiometric calculations to derive the solution pH. The second example addresses a weak acid titration requiring equilibrium calculations.

 

Example 14.21

Calculating pH for Titration Solutions: Strong Acid/Strong Base

A titration is carried out for 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M of a strong base NaOH (the titration curve is shown in Figure 14.18). Calculate the pH at these volumes of added base solution:

(a) 0.00 mL

(b) 12.50 mL

(c) 25.00 mL

(d) 37.50 mL

Solution

(a) Titrant volume = 0 mL. The solution pH is due to the acid ionization of HCl. Because this is a strong acid, the ionization is complete and the hydronium ion molarity is 0.100 M. The pH of the solution is then

pH = − log (0.100) = 1.000

(b) Titrant volume = 12.50 mL. Since the acid sample and the base titrant are both monoprotic and equally concentrated, this titrant addition involves less than a stoichiometric amount of base, and so it is completely consumed by reaction with the excess acid in the sample. The concentration of acid remaining is computed by subtracting the consumed amount from the intial amount and then dividing by the solution volume:

[H₃O⁺] = [latex]\frac{n(H^{+})}{V} = \frac{0.002500 \text{mol} \times ( \frac{1000 \text{mL}}{1 L} ) - 0.100 M \times 12.50 \text{mL}}{25.00 \text{mL} + 12.50 \text{mL}}[/latex] = 0.0333 M

(c) Titrant volume = 25.00 mL. This titrant addition involves a stoichiometric amount of base (the equivalence point), and so only products of the neutralization reaction are in solution (water and NaCl). Neither the cation nor the anion of this salt undergo acid-base ionization; the only process generating hydronium ions is the autoprotolysis of water. The solution is neutral, having a pH = 7.00.

(d) Titrant volume = 37.50 mL. This involves the addition of titrant in excess of the equivalence point. The solution pH is then calculated using the concentration of hydroxide ion:

n(OH⁻)₀ > n(H⁺)₀

[OH^–] = [latex]\frac{n(OH^{-})}{V} = \frac{0.100 M \times 35.70 \text{mL} - 0.002500 \text{mol} \times ( \frac{1000 \text{mL}}{1 L} ) }{25.00 \text{mL} + 37.50 \text{mL}}[/latex] = 0.0200 M

pH = 14 – pOH = 14 + log([OH^–]) = 14 + log(0.0200) = 12.30

Check Your Learning

Calculate the pH for the strong acid/strong base titration between 50.0 mL of 0.100 M HNO₃(aq) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 40.0 mL.

Answer: 0.00: 1.000; 15.0: 1.5111; 25.0: 7; 40.0: 12.523

 

 

Example 14.22

Titration of a Weak Acid with a Strong Base

Consider the titration of 25.00 mL of 0.100 M CH₃CO₂H with 0.100 M NaOH. The reaction can be represented as:

CH₃CO₂H + OH⁻ ⟶ CH₃CO₂ ⁻ + H₂O

Calculate the pH of the titration solution after the addition of the following volumes of NaOH titrant:

(a) 0.00 mL

(b) 25.00 mL

(c) 12.50 mL

(d) 37.50 mL

 

Solution

(a) The initial pH is computed for the acetic acid solution in the usual ICE approach:

K_a = [latex]\frac{[H_{3}O^{+}][CH_{3}CO_{2}^{-}]}{[CH_{3}CO_{2}H]}[/latex] ≈ [latex]\frac{[H_{3}O^{+}]^{2}}{[CH_{3}CO_{2}H]_{0}}[/latex],

[H₃O⁺] = [latex]sqrt{\text{K}_{a} \times [CH_{3}CO_{2}H]} = \sqrt{1.8 \times 10^{-5} \times 0.100} = 1.3 \times 10^{-3}[/latex]

pH = -log(1.3 x 10^-3) = 2.87

 

(b) The acid and titrant are both monoprotic and the sample and titrant solutions are equally concentrated; thus, this volume of titrant represents the equivalence point. Unlike the strong-acid example above, however, the reaction mixture in this case contains a weak conjugate base (acetate ion). The solution pH is computed considering the base ionization of acetate, which is present at a concentration of

[latex]\frac{0.00250 \text{mol}}{0.0500 L}[/latex] = 0.0500 MCH₃CO₂^–

Base ionization of acetate is represented by the equation

CH₃CO₂ ⁻(aq) + H₂O(l) ⇌ CH₃CO₂ H(aq) + OH⁻(aq)

K_b = [latex]\frac{[H^{+}][OH^{-}]}{K_{a}} = \frac{K_{w}}{K_{a}} = \frac{1.0 \times 10^{-14}}{1.8 \times 10^{-5}} = 5.6 \times 10^{-10}[/latex]

 

Assuming x << 0.0500, the pH may be calculated via the usual ICE approach: Kb = [latex]\frac{x^{2}}{0.0500 M}[/latex]

x = [OH^–] = 5.3 x 10^-6

pOH = -log(5.3 x 10^-6) = 5.28

pH = 14.00 – 5.28 = 8.72

Note that the pH at the equivalence point of this titration is significantly greater than 7, as expected when titrating a weak acid with a strong base.

(c) Titrant volume = 12.50 mL. This volume represents one-half of the stoichiometric amount of titrant, and so one-half of the acetic acid has been neutralized to yield an equivalent amount of acetate ion. The concentrations of these conjugate acid-base partners, therefore, are equal. A convenient approach to computing the pH is use of the Henderson-Hasselbalch equation:

pH = pK_a + log[latex]\frac{[Base]}{[Acid]}[/latex] = -log(K_a) + log[latex]\frac{[CH_{3}CO_{2}^{-}]}{[CH_{3}CO_{2}H]}[/latex] = -log(1.8 x 10^-5) + log(1)

pH = -log(1.8 x 10^-5) = 4.74

(pH = pK_a at the half-equivalence point in a titration of a weak acid)

(d) Titrant volume = 37.50 mL. This volume represents a stoichiometric excess of titrant, and a reaction solution containing both the titration product, acetate ion, and the excess strong titrant. In such solutions, the solution pH is determined primarily by the amount of excess strong base:

[OH^–] = [latex]\frac{(0.003750 \text{mol} - 0.00250 \text{mol})}{0.06250 \text{L}}[/latex] = 2.00 x 10^-2 M

pOH = -log(2.00 x 10^-2) = 1.70, and pH = 14.00 – 1.70 = 12.30

Check Your Learning

Calculate the pH for the weak acid/strong base titration between 50.0 mL of 0.100 M HCOOH(aq) (formic acid) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 30.0 mL.

Answer: 0.00 mL: 2.37; 15.0 mL: 3.92; 25.00 mL: 8.29; 30.0 mL: 12.097

 

Performing additional calculations similar to those in the preceding example permits a more full assessment of titration curves. A summary of pH/volume data pairs for the strong and weak acid titrations is provided in Table 14.2 and plotted as titration curves in Figure 14.18. A comparison of these two curves illustrates several important concepts that are best addressed by identifying the four stages of a titration:

1. initial state (added titrant volume = 0 mL): pH is determined by the acid being titrated; because the two acid samples are equally concentrated, the weak acid will exhibit a greater initial pH
2. pre-equivalence point (0 mL < V < 25 mL): solution pH increases gradually and the acid is consumed by reaction with added titrant; composition includes unreacted acid and the reaction product, its conjugate base
3. equivalence point (V = 25 mL): a drastic rise in pH is observed as the solution composition transitions from acidic to either neutral (for the strong acid sample) or basic (for the weak acid sample), with pH determined by ionization of the conjugate base of the acid
4. postequivalence point (V > 25 mL): pH is determined by the amount of excess strong base titrant added; since both samples are titrated with the same titrant, both titration curves appear similar at this stage.

pH Values in the Titrations of a Strong Acid and of a Weak Acid

Table 14.2

---

1. Titration of 25.00 mL of 0.100 M HCl (0.00250 mol of HCI) with 0.100 M NaOH.

2. Titration of 25.00 mL of 0.100 M CH₃CO₂H (0.00250 mol of CH₃CO₂H) with 0.100 M NaOH.

 

 

 

 

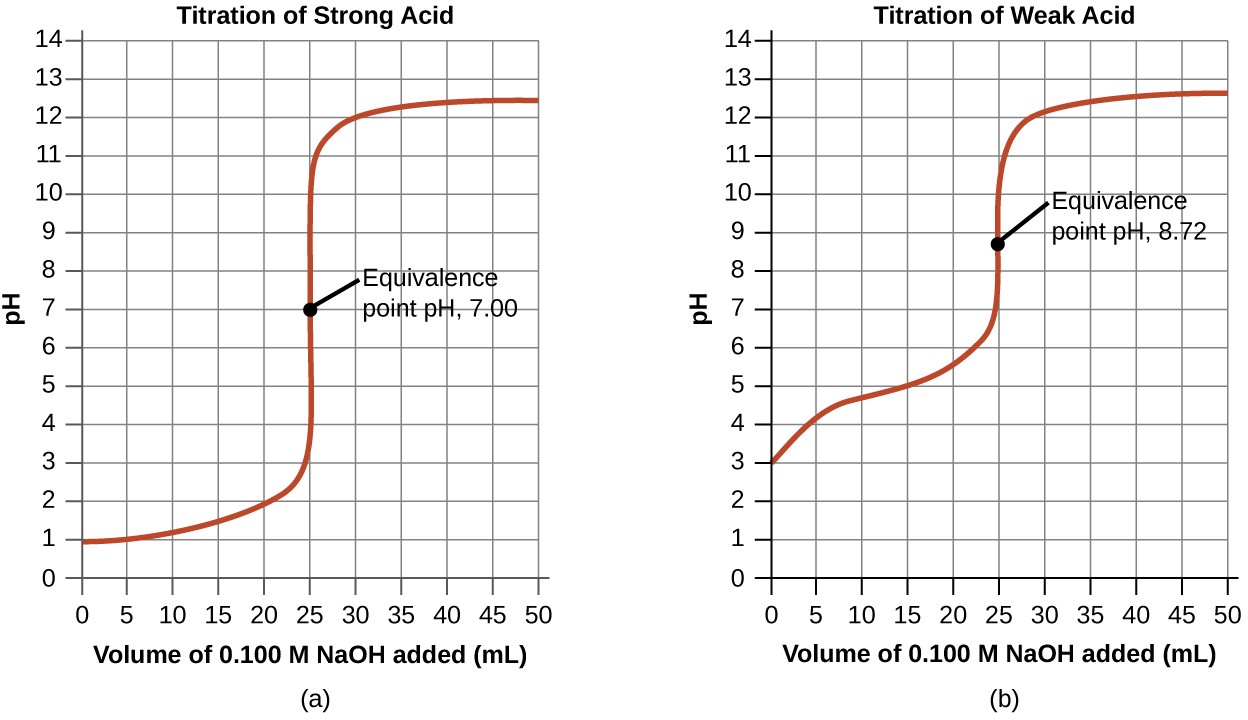
Figure 14.18 (a) The titration curve for the titration of 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M NaOH (strong base) has an equivalence point of 7.00 pH. (b) The titration curve for the titration of 25.00 mL of 0.100 M acetic acid (weak acid) with 0.100 M NaOH (strong base) has an equivalence point of 8.72 pH.

 

 

Acid-Base Indicators

Certain organic substances change color in dilute solution when the hydronium ion concentration reaches a particular value. For example, phenolphthalein is a colorless substance in any aqueous solution with a hydronium ion concentration greater than 5.0 × 10⁻⁹ M (pH < 8.3). In more basic solutions where the hydronium ion concentration is less than 5.0 × 10⁻⁹ M (pH > 8.3), it is red or pink. Substances such as phenolphthalein, which can be used to determine the pH of a solution, are called acid-base indicators. Acid-base indicators are either weak organic acids or weak organic bases.

The equilibrium in a solution of the acid-base indicator methyl orange, a weak acid, can be represented by an equation in which we use HIn as a simple representation for the complex methyl orange molecule:

HIn(aq) + H₂O(l) ⇌ H₃O⁺(aq) + In⁻(aq)

Red                                                  Yellow

K_a = [latex]\frac{[H_{3}O^{+}][In^{-}]}{[HIn]}[/latex] = 4.0 x 10^-4

The anion of methyl orange, In−, is yellow, and the nonionized form, HIn, is red. When we add acid to a solution of methyl orange, the increased hydronium ion concentration shifts the equilibrium toward the nonionized red form, in accordance with Le Châtelier’s principle. If we add base, we shift the equilibrium towards the yellow form. This behavior is completely analogous to the action of buffers.

The perceived color of an indicator solution is determined by the ratio of the concentrations of the two species In− and HIn. If most of the indicator (typically about 60−90% or more) is present as In−, the perceived color of the solution is yellow. If most is present as HIn, then the solution color appears red. The Henderson-Hasselbalch equation is useful for understanding the relationship between the pH of an indicator solution and its composition (thus, perceived color):

pH = pK_a + log[latex]( \frac{[In^{-}]}{[HIn]} )[/latex]

In solutions where pH > pK_a, the logarithmic term must be positive, indicating an excess of the conjugate base form of the indicator (yellow solution). When pH > pK_a, the log term must be negative, indicating an excess of the conjugate acid (red solution). When the solution pH is close to the indicator pKa, appreciable amounts of both conjugate partners are present, and the solution color is that of an additive combination of each (yellow and red, yielding orange). The color change interval (or pH interval) for an acid-base indicator is defined as the range of pH values over which a change in color is observed, and for most indicators this range is approximately p K_a ± 1.

There are many different acid-base indicators that cover a wide range of pH values and can be used to determine the approximate pH of an unknown solution by a process of elimination. Universal indicators and pH paper contain a mixture of indicators and exhibit different colors at different pHs. Figure 14.19 presents several indicators, their colors, and their color-change intervals.

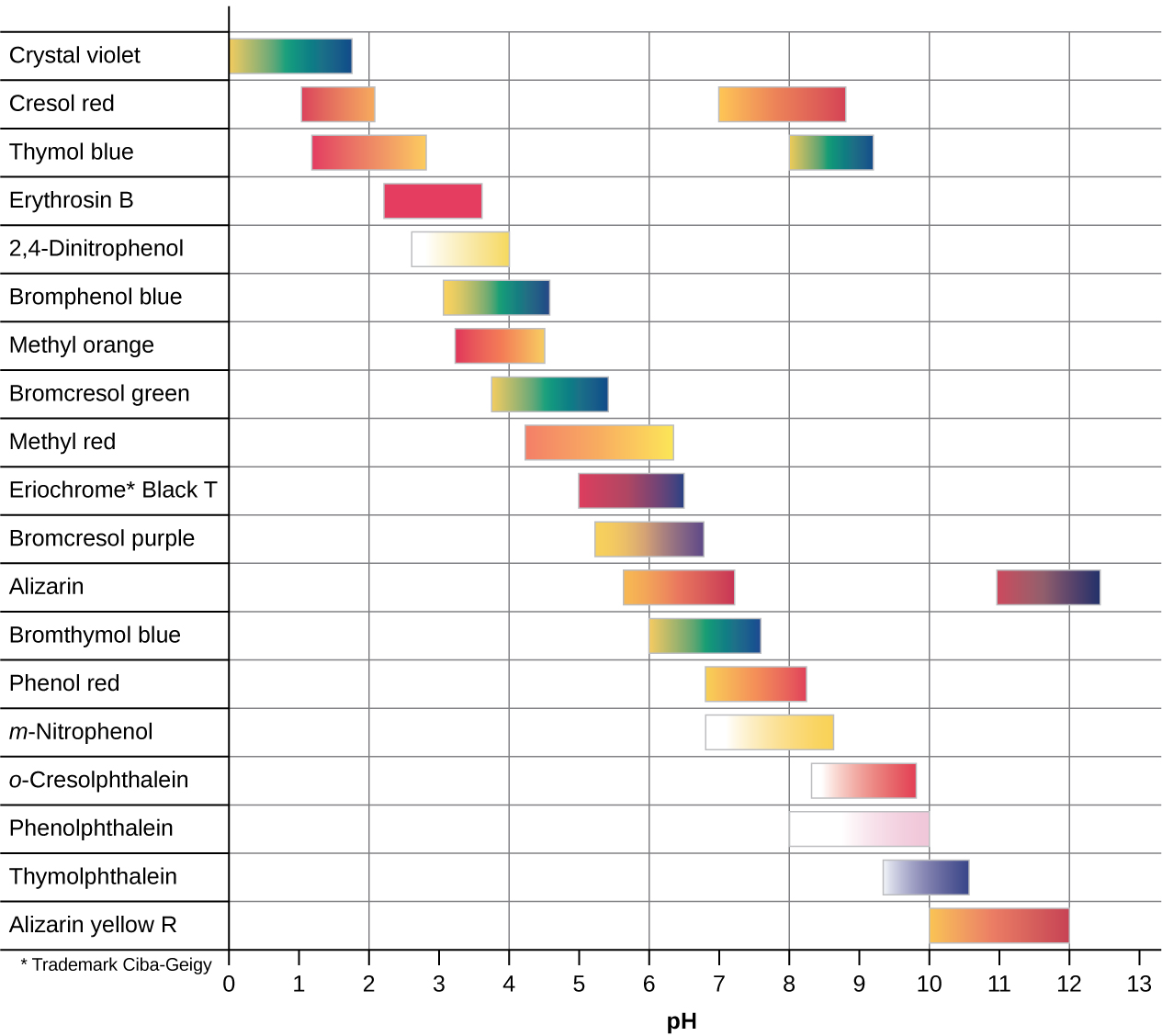
Figure 14.19 This chart illustrates the color change intervals for several acid-base indicators.

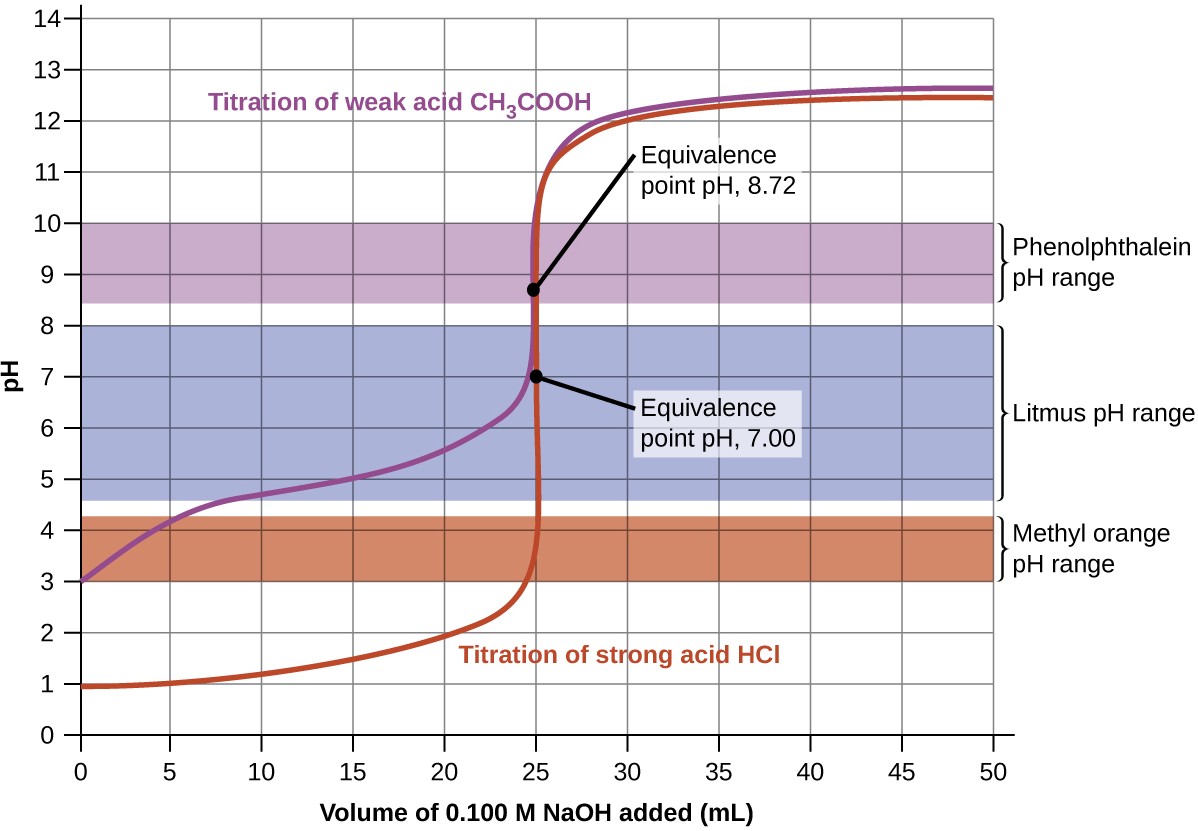
Figure 14.20 Titration curves for strong and weak acids illustrating the proper choice of acid-base indicator. Any of the three indicators will exhibit a reasonably sharp color change at the equivalence point of the strong acid titration, but only phenolphthalein is suitable for use in the weak acid titration.

The titration curves shown in Figure 14.20 illustrate the choice of a suitable indicator for specific titrations. In the strong acid titration, use of any of the three indicators should yield reasonably sharp color changes and accurate end point determinations. For this titration, the solution pH reaches the lower limit of the methyl orange color change interval after addition of ~24 mL of titrant, at which point the initially red solution would begin to appear orange. When 25 mL of titrant has been added (the equivalence point), the pH is well above the upper limit and the solution will appear yellow. The titration’s end point may then be estimated as the volume of titrant that yields a distinct orange-to-yellow color change. This color change would be challenging for most human eyes to precisely discern. More-accurate estimates of the titration end point are possible using either litmus or phenolphthalein, both of which exhibit color change intervals that are encompassed by the steep rise in pH that occurs around the 25.00 mL equivalence point.

The weak acid titration curve in Figure 14.20 shows that only one of the three indicators is suitable for end point detection. If methyl orange is used in this titration, the solution will undergo a gradual red-to-orange-to-yellow color change over a relatively large volume interval (0–6 mL), completing the color change well before the equivalence point (25 mL) has been reached. Use of litmus would show a color change that begins after adding 7 – 8 mL of titrant and ends just before the equivalence point. Phenolphthalein, on the other hand, exhibits a color change interval that nicely brackets the abrupt change in pH occurring at the titration’s equivalence point. A sharp color change from colorless to pink will be observed within a very small volume interval around the equivalence point.

Key Terms

acid ionization reaction involving the transfer of a proton from an acid to water, yielding hydronium ions and the conjugate base of the acid

acid ionization constant (K_a) equilibrium constant for an acid ionization reaction

acid-base indicator weak acid or base whose conjugate partner imparts a different solution color; used in visual assessments of solution pH

acidic a solution in which [H₃O⁺] > [OH⁻]

amphiprotic species that may either donate or accept a proton in a Bronsted-Lowry acid-base reaction

amphoteric species that can act as either an acid or a base

autoionization reaction between identical species yielding ionic products; for water, this reaction involves transfer of protons to yield hydronium and hydroxide ions

base ionization reaction involving the transfer of a proton from water to a base, yielding hydroxide ions and the conjugate acid of the base

base ionization constant (K_b) equilibrium constant for a base ionization reaction

basic a solution in which [H₃O⁺] < [OH⁻]

Brønsted-Lowry acid  Proton donor

Brønsted-Lowry base Proton acceptor

buffer mixture of appreciable amounts of a weak acid-base pair the pH of a buffer resists change when small amounts of acid or base are added

buffer capacity amount of an acid or base that can be added to a volume of a buffer solution before its pH changes significantly (usually by one pH unit)

color-change interval range in pH over which the color change of an indicator is observed

conjugate acid substance formed when a base gains a proton

conjugate base substance formed when an acid loses a proton

diprotic acid acid containing two ionizable hydrogen atoms per molecule

diprotic base base capable of accepting two protons

Henderson-Hasselbalch equation logarithmic version of the acid ionization constant expression, conveniently formatted for calculating the pH of buffer solutions

ion-product constant for water (K_w) equilibrium constant for the autoionization of water

leveling effect observation that acid-base strength of solutes in a given solvent is limited to that of the solvent’s characteristic acid and base species (in water, hydronium and hydroxide ions, respectively)

monoprotic acid acid containing one ionizable hydrogen atom per molecule

neutral describes a solution in which [H₃O⁺] = [OH⁻]

oxyacid ternary compound with acidic properties, molecules of which contain a central nonmetallic atom bonded to one or more O atoms, at least one of which is bonded to an ionizable H atom

percent ionization ratio of the concentration of ionized acid to initial acid concentration expressed as a percentage

pH logarithmic measure of the concentration of hydronium ions in a solution

pOH logarithmic measure of the concentration of hydroxide ions in a solution

stepwise ionization process in which a polyprotic acid is ionized by losing protons sequentially

titration curve plot of some sample property (such as pH) versus volume of added titrant

triprotic acid acid that contains three ionizable hydrogen atoms per molecule

Key Equations

• K_w = [H₃O⁺][OH⁻] = 1.0 × 10⁻¹⁴ (at 25 °C)
• pH = −log[H₃O⁺]
• pOH = −log[OH⁻]
• [H₃O+] = 10^−pH
• [OH−] = 10^−pOH
• pH + pOH = pK_w = 14.00 at 25 °C
• K_a = [latex]\frac{[H_{3}O^{+}][A^{-}]}{[HA]}[/latex]
• K_b = [latex]\frac{[HB^{+}][OH^{-}]}{[B]}[/latex]
• K_a × K_b = 1.0 × 10⁻¹⁴ = K_w
• Percent ionization = [latex]\frac{[H_{3}O^{+}]\text{eq}}{[HA]_{0}}[/latex] x 100
• pK_a = −log K_a
• pK_b = −log K_b
• pH = pKa + log $latex \frac{[A^{-}]}{[HA]}

Summary

Brønsted-Lowry Acids and Bases

A compound that can donate a proton (a hydrogen ion) to another compound is called a Brønsted-Lowry acid. The compound that accepts the proton is called a Brønsted-Lowry base. The species remaining after a Brønsted-Lowry acid has lost a proton is the conjugate base of the acid. The species formed when a Brønsted-Lowry base gains a proton is the conjugate acid of the base. Thus, an acid-base reaction occurs when a proton is transferred from an acid to a base, with formation of the conjugate base of the reactant acid and formation of the conjugate acid of the reactant base. Amphiprotic species can act as both proton donors and proton acceptors. Water is the most important amphiprotic species. It can form both the hydronium ion, H₃O+, and the hydroxide ion, OH− when it undergoes autoionization:

2H₂O(l) ⇌ H₃O⁺(aq) + OH⁻(aq)

The ion product of water, K_w is the equilibrium constant for the autoionization reaction:

K_w = [H₃O⁺][OH⁻] = 1.0 × 10⁻¹⁴ at 25 °C

Concentrations of hydronium and hydroxide ions in aqueous media are often represented as logarithmic pH and pOH values, respectively. At 25 °C, the autoprotolysis equilibrium for water requires the sum of pH and pOH to equal 14 for any aqueous solution. The relative concentrations of hydronium and hydroxide ion in a solution define its status as acidic ([H₃O+] > [OH−]), basic ([H₃O+] < [OH−]), or neutral ([H₃O+] = [OH−]). At 25 °C, a pH < 7 indicates an acidic solution, a pH > 7 a basic solution, and a pH = 7 a neutral solution.

Relative Strengths of Acids and Bases

The relative strengths of acids and bases are reflected in the magnitudes of their ionization constants; the stronger the acid or base, the larger its ionization constant. A reciprocal relation exists between the strengths of a conjugate acid-base pair: the stronger the acid, the weaker its conjugate base. Water exerts a leveling effect on dissolved acids or bases, reacting completely to generate its characteristic hydronium and hydroxide ions (the strongest acid and base that may exist in water). The strengths of the binary acids increase from left to right across a period of the periodic table (CH₄ < NH₃ < H₂O < HF), and they increase down a group (HF < HCl < HBr < HI). The strengths of oxyacids that contain the same central element increase as the oxidation number of the element increases (H₂SO₃ < H₂SO₄). The strengths of oxyacids also increase as the electronegativity of the central element increases [H ₂SeO₄ < H₂SO₄].

Hydrolysis of Salts

The ions composing salts may possess acidic or basic character, ionizing when dissolved in water to yield acidic or basic solutions. Acidic cations are typically the conjugate partners of weak bases, and basic anions are the conjugate partners of weak acids. Many metal ions bond to water molecules when dissolved to yield complex ions that may function as acids.

Polyprotic Acids

An acid that contains more than one ionizable proton is a polyprotic acid. These acids undergo stepwise ionization reactions involving the transfer of single protons. The ionization constants for polyprotic acids decrease with each subsequent step; these decreases typically are large enough to permit simple equilibrium calculations that treat each step separately.

Buffers

Solutions that contain appreciable amounts of a weak conjugate acid-base pair are called buffers. A buffered solution will experience only slight changes in pH when small amounts of acid or base are added. Addition of large amounts of acid or base can exceed the buffer capacity, consuming most of one conjugate partner and preventing further buffering action.

Acid-Base Titrations

The titration curve for an acid-base titration is typically a plot of pH versus volume of added titrant. These curves are useful in selecting appropriate acid-base indicators that will permit accurate determinations of titration end points.

Exercises

Brønsted-Lowry Acids and Bases

1. Write equations that show NH₃ as both a conjugate acid and a conjugate base.
2. Write equations that show H₂ PO₄ ⁻ acting both as an acid and as a base.
3. Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry acid:
   1. H₃O⁺
   2. HCl
   3. NH₃
   4. CH₃CO₂H
   5. NH₄ ⁺
   6. HSO₄ ⁻
4. Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry acid:
   1. HNO₃
   2. PH₄ ⁺
   3. H₂S
   4. CH₃CH₂COOH
   5. H₂PO₄ ⁻
   6. HS⁻
5. Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry base:
   1. H₂O
   2. OH⁻
   3. NH₃
   4. CN⁻
   5. S²⁻
   6. H₂PO₄ ⁻
6. Show by suitable net ionic equations that each of the following species can act as a Brønsted-Lowry base:
   1. HS−
   2. PO₄ ³⁻
   3. NH₂ ⁻
   4. C₂H₅OH
   5. O₂⁻
   6. H₂PO₄ ⁻
7. What is the conjugate acid of each of the following? What is the conjugate base of each?
   1. OH⁻
   2. H₂O
   3. HCO₃ ⁻
   4. NH₃
   5. HSO₄ ⁻
   6. H₂O₂
   7. HS⁻
   8. H5 N2 +
8. What is the conjugate acid of each of the following? What is the conjugate base of each?
   1. H₂S
   2. H₂PO₄ ⁻
   3. PH₃
   4. HS⁻
   5. HSO3 −
   6. H3 O2 +
   7. H₄N₂
   8. CH₃OH
9. Identify and label the Brønsted-Lowry acid, its conjugate base, the Brønsted-Lowry base, and its conjugate acid in each of the following equations:
   1. HNO₃ + H₂O ⟶ H₃O⁺ + NO₃ ⁻
   2. CN⁻ + H₂O ⟶ HCN + OH⁻
   3. H₂SO₄ + Cl⁻ ⟶ HCl + HSO₄ ⁻
   4. HSO₄ ⁻ + OH⁻ ⟶ SO₄ ²⁻ + H₂O
   5. O₂⁻ + H₂O ⟶ 2OH⁻
   6. [Cu(H₂O)₃(OH)]⁺ + [Al(H₂O)₆]³⁺ ⟶ [Cu(H₂O)₄]²⁺ + [Al(H₂O)₅(OH)]²⁺
   7. H₂S + NH₂ ⁻ ⟶ HS⁻ + NH₃
10. Identify and label the Brønsted-Lowry acid, its conjugate base, the Brønsted-Lowry base, and its conjugate acid in each of the following equations:
    1. NO₂ ⁻ + H₂O ⟶ HNO₂ + OH⁻
    2. HBr + H₂O ⟶ H₃O⁺ + Br⁻
    3. HS⁻ + H₂O ⟶ H₂S + OH⁻
    4. H₂PO₄ − + OH− ⟶ HPO₄ ²⁻ + H2 O
    5. H₂PO₄ − + HCl ⟶ H₃PO₄ + Cl⁻
    6. [Fe(H₂O)₅(OH)]²⁺ + [Al(H₂O)₆]³⁺ ⟶ [Fe(H₂O)₆]³⁺ + [Al(H₂O)₅(OH)]²⁺
    7. CH₃OH + H⁻ ⟶ CH₃O⁻ + H₂
11. What are amphiprotic species? Illustrate with suitable equations.
12. State which of the following species are amphiprotic and write chemical equations illustrating the amphiprotic character of these species:
    1. H₂O
    2. H₂PO₄ ⁻
    3. S²⁻
    4. CO₃ ²⁻
    5. HSO₄ ⁻
13. State which of the following species are amphiprotic and write chemical equations illustrating the amphiprotic character of these species.
    1. NH₃
    2. HPO₄ −
    3. Br⁻
    4. NH₄ ⁺
    5. ASO₄ ³⁻
14. Is the self-ionization of water endothermic or exothermic? The ionization constant for water ( K_w) is 2.9 × 10⁻¹⁴ at 40 °C and 9.3 × 10⁻¹⁴ at 60 °C.
15. Explain why a sample of pure water at 40 °C is neutral even though [H₃O⁺] = 1.7 × 10⁻⁷ M. K_w is 2.9 × 10−14 at 40 °C.
16. The ionization constant for water (K_w) is 2.9 × 10⁻¹⁴ at 40 °C. Calculate [H₃O⁺], [OH⁻], pH, and pOH for pure water at 40 °C.
17. The ionization constant for water (K_w) is 9.311 × 10⁻¹⁴ at 60 °C. Calculate [H₃O⁺], [OH⁻], pH, and pOH for pure water at 60 °C.
18. Calculate the pH and the pOH of each of the following solutions at 25 °C for which the substances ionize completely:
    1. 0.200 M HCl
    2. 0.0143 M NaOH
    3. 3.0 M HNO₃
    4. 0.0031 M Ca(OH)₂
19. Calculate the pH and the pOH of each of the following solutions at 25 °C for which the substances ionize completely:
    1. 0.000259 M HClO₄
    2. 0.21 M NaOH
    3. 0.000071 M Ba(OH)₂
    4. 2.5 M KOH
20. What are the pH and pOH of a solution of 2.0 M HCl, which ionizes completely?
21. What are the hydronium and hydroxide ion concentrations in a solution whose pH is 6.52?
22. Calculate the hydrogen ion concentration and the hydroxide ion concentration in wine from its pH. See Figure 14.2 for useful information.
23. Calculate the hydronium ion concentration and the hydroxide ion concentration in lime juice from its pH. See Figure 14.2 for useful information.
24. The hydronium ion concentration in a sample of rainwater is found to be 1.7 × 10⁻⁶ M at 25 °C. What is the concentration of hydroxide ions in the rainwater?
25. The hydroxide ion concentration in household ammonia is 3.2 × 10⁻³ M at 25 °C. What is the concentration of hydronium ions in the solution?
26. Explain why the neutralization reaction of a strong acid and a weak base gives a weakly acidic solution.
27. Explain why the neutralization reaction of a weak acid and a strong base gives a weakly basic solution.
28. Use this list of important industrial compounds (and Figure 14.8) to answer the following questions regarding: CaO, Ca(OH)₂, CH₃CO₂H, CO_2, HCl, H₂CO₃, HF, HNO₂, HNO₃, H₃PO₄, H₂SO₄, NH₃, NaOH, Na₂CO₃.
    1. Identify the strong Brønsted-Lowry acids and strong Brønsted-Lowry bases.
    2. List those compounds in (a) that can behave as Brønsted-Lowry acids with strengths lying between those of H₃O+ and H₂O.
    3. List those compounds in (a) that can behave as Brønsted-Lowry bases with strengths lying between those of H ₂O and OH−.
29. The odor of vinegar is due to the presence of acetic acid, CH₃CO₂H, a weak acid. List, in order of descending concentration, all of the ionic and molecular species present in a 1-M aqueous solution of this acid.
30. Household ammonia is a solution of the weak base NH₃ in water. List, in order of descending concentration, all of the ionic and molecular species present in a 1-M aqueous solution of this base.
31. Explain why the ionization constant, K_a, for H₂SO₄ is larger than the ionization constant for H₂SO₃.
32. Explain why the ionization constant, K_a, for HI is larger than the ionization constant for HF.
33. Gastric juice, the digestive fluid produced in the stomach, contains hydrochloric acid, HCl. Milk of Magnesia, a suspension of solid Mg(OH)₂ in an aqueous medium, is sometimes used to neutralize excess stomach acid. Write a complete balanced equation for the neutralization reaction, and identify the conjugate acid-base pairs.
34. Nitric acid reacts with insoluble copper(II) oxide to form soluble copper(II) nitrate, Cu(NO₃)₂, a compound that has been used to prevent the growth of algae in swimming pools. Write the balanced chemical equation for the reaction of an aqueous solution of HNO₃ with CuO.
35. What is the ionization constant at 25 °C for the weak acid CH3 NH3 +, the conjugate acid of the weak base CH₃NH₂, K_b = 4.4 × 10⁻⁴.
36. What is the ionization constant at 25 °C for the weak acid (CH3)2 NH2 +, the conjugate acid of the weak base (CH₃)₂NH, K_b = 5.9 × 10⁻⁴?
37. Which base, CH₃NH₂ or (CH₃)₂NH, is the stronger base? Which conjugate acid, (CH3)2 NH2 + or CH3 NH3 + , is the stronger acid?
38. Which is the stronger acid, NH4 + or HBrO?
39. Which is the stronger base, (CH₃)₃N or H2 BO3 − ?
40. Predict which acid in each of the following pairs is the stronger and explain your reasoning for each.
    1. H₂O or HF
    2. B(OH)₃ or Al(OH)₃
    3. HSO3 − or HSO4 −
    4. NH₃ or H₂S
    5. H₂O or H₂Te
41. Predict which compound in each of the following pairs of compounds is more acidic and explain your reasoning for each.
    1. HSO₄ ⁻ or HSeO₄ ⁻
    2. NH₃ or H₂O
    3. PH₃ or HI
    4. NH₃ or PH₃
    5. H₂S or HBr
42. Rank the compounds in each of the following groups in order of increasing acidity or basicity, as indicated, and explain the order you assign.
    1. acidity: HCl, HBr, HI
    2. basicity: H₂O, OH⁻, H⁻, Cl⁻
    3. basicity: Mg(OH)₂, Si(OH)₄, ClO₃(OH) (Hint: Formula could also be written as HClO₄.)
    4. acidity: HF, H₂O, NH₃, CH₄
43. Rank the compounds in each of the following groups in order of increasing acidity or basicity, as indicated, and explain the order you assign.
    1. acidity: NaHSO₃, NaHSeO₃, NaHSO₄
    2. basicity: BrO₂ ⁻, ClO₂ ⁻, IO₂ ⁻
    3. acidity: HOCl, HOBr, HOI
    4. acidity: HOCl, HOClO, HOClO₂, HOClO₃
    5. basicity: NH₂ ⁻, HS⁻, HTe⁻, PH₂ ⁻
    6. basicity: BrO⁻, BrO₂ ⁻, BrO₃ ⁻, BrO₄ ⁻
44. Both HF and HCN ionize in water to a limited extent. Which of the conjugate bases, F− or CN−, is the stronger base?
45. The active ingredient formed by aspirin in the body is salicylic acid, C₆H₄OH(CO₂H). The carboxyl group (−CO₂H) acts as a weak acid. The phenol group (an OH group bonded to an aromatic ring) also acts as an acid but a much weaker acid. List, in order of descending concentration, all of the ionic and molecular species present in a 0.001-M aqueous solution of C₆H₄OH(CO₂H).
46. Are the concentrations of hydronium ion and hydroxide ion in a solution of an acid or a base in water directly proportional or inversely proportional? Explain your answer.
47. What two common assumptions can simplify calculation of equilibrium concentrations in a solution of a weak acid or base?
48. Which of the following will increase the percent of NH₃ that is converted to the ammonium ion in water?
    1. addition of NaOH
    2. addition of HCl
    3. addition of NH₄Cl
49. Which of the following will increase the percentage of HF that is converted to the fluoride ion in water?
    1. addition of NaOH
    2. addition of HCl
    3. addition of NaF
50. What is the effect on the concentrations of NO₂ ⁻, HNO₂, and OH− when the following are added to a solution of KNO₂ in water:
    1. HCl
    2. HNO₂
    3. NaOH
    4. NaCl
    5. KNO
51. What is the effect on the concentration of hydrofluoric acid, hydronium ion, and fluoride ion when the following are added to separate solutions of hydrofluoric acid?
    1. HCl
    2. KF
    3. NaCl
    4. KOH
    5. HF
52. Why is the hydronium ion concentration in a solution that is 0.10 M in HCl and 0.10 M in HCOOH determined by the concentration of HCl?
53. From the equilibrium concentrations given, calculate K_a for each of the weak acids and K_b for each of the weak bases.
    1. CH₃CO₂H: [H₃ O⁺] = 1.34 × 10⁻³ M;
       [CH₃ CO₂ ⁻] = 1.34 × 10⁻³ M;
       [CH₃CO₂H] = 9.866 × 10⁻² M
    2. ClO⁻: [OH⁻] = 4.0 × 10⁻⁴M;
       [HClO] = 2.38 × 10⁻⁴ M;
       [ClO⁻] = 0.273 M;
    3. HCO₂H: [HCO₂H] = 0.524 M;
       [H₃ O⁺] = 9.8 × 10⁻³ M;
       [HCO₂ ⁻] = 9.8 × 10⁻³ M;
    4. C₆ H₅ NH₃ ⁺ : [C₆ H₅ NH₃ ⁺] = 0.233 M;
       [C₆H₅NH₂] = 2.3 × 10⁻³ M;

       [H₃ O⁺] = 2.3 × 10⁻³ M

54. From the equilibrium concentrations given, calculate K_a for each of the weak acids and K_b for each of the weak bases.
    1. NH₃: [OH⁻] = 3.1 × 10⁻³ M;
       [NH₄ ⁺] = 3.1 × 10⁻³ M;
       [NH₃] = 0.533 M;
    2. HNO₂: [H₃O⁺] = 0.011 M;
       [NO₂ ⁻] = 0.0438 M;
       [HNO₂] = 1.07 M;
    3. (CH₃)₃N: [(CH₃)₃N] = 0.25 M;
       [(CH₃)₃NH⁺] = 4.3 × 10⁻³ M;
       [OH⁻] = 3.7 × 10⁻³ M;
    4. NH₄ ⁺ : [NH₄ ⁺] = 0.100 M;
       [NH₃] = 7.5 × 10⁻⁶ M;
       [H₃O⁺] = 7.5 × 10⁻⁶ M
55. Determine K_b for the nitrite ion, NO₂ ⁻. In a 0.10-M solution this base is 0.0015% ionized.
56. Determine K_a for hydrogen sulfate ion, HSO₄ ⁻. In a 0.10-M solution the acid is 29% ionized.
57. Calculate the ionization constant for each of the following acids or bases from the ionization constant of its conjugate base or conjugate acid:
    1. F⁻
    2. NH₄ ⁺
    3. AsO₄ ³⁻
    4. (CH₃)₂ NH₂ ⁺
    5. NO₂ ⁻
    6. HC₂O₄ ⁻ (as a base)
58. Calculate the ionization constant for each of the following acids or bases from the ionization constant of its conjugate base or conjugate acid:
    1. HTe⁻ (as a base)
    2. (CH₃)₃ NH⁺
    3. HAsO₄ ³⁻ (as a base)
    4. HO₂ ⁻ (as a base)
    5. C₆H₅ NH₃ ⁺
    6. HSO₃ ⁻ (as a base)
59. Using the K_a value of 1.4 × 10⁻⁵, place Al(H₂ O)₆ ³⁺ in the correct location in Figure14.7.
60. Calculate the concentration of all solute species in each of the following solutions of acids or bases. Assume that the ionization of water can be neglected, and show that the change in the initial concentrations can be neglected.
    1. 0.0092 M HClO, a weak acid
    2. 0.0784 M C₆H₅NH₂, a weak base
    3. 0.0810 M HCN, a weak acid
    4. 0.11 M (CH₃)₃N, a weak base
    5. 0.120 M Fe(H₂O)₆ ²⁺ a weak acid, K_a = 1.6 × 10⁻⁷
61. Propionic acid, C₂H₅CO₂H (K_a = 1.34 × 10⁻⁵), is used in the manufacture of calcium propionate, a food preservative. What is the pH of a 0.698-M solution of C₂H₅CO₂H?
62. White vinegar is a 5.0% by mass solution of acetic acid in water. If the density of white vinegar is 1.007 g/cm3, what is the pH?
63. The ionization constant of lactic acid, CH₃CH(OH)CO₂H, an acid found in the blood after strenuous exercise, is 1.36 × 10⁻⁴. If 20.0 g of lactic acid is used to make a solution with a volume of 1.00 L, what is the concentration of hydronium ion in the solution?
64. Nicotine, C₁₀H₁₄N₂, is a base that will accept two protons (K_b1 = 7 × 10⁻⁷, K_b2 = 1.4 × 10⁻¹¹). What is the concentration of each species present in a 0.050-M solution of nicotine?
65. The pH of a 0.23-M solution of HF is 1.92. Determine K_a for HF from these data.
66. The pH of a 0.15-M solution of HSO4 − is 1.43. Determine K_a for HSO4 − from these data.
67. The pH of a 0.10-M solution of caffeine is 11.70. Determine K_b for caffeine from these data: C₈H₁₀N₄O₂(aq) + H₂O(l) ⇌ C₈H₁₀N₄O₂H⁺(aq) + OH⁻(aq)
68. The pH of a solution of household ammonia, a 0.950 M solution of NH_3, is 11.612. Determine K_b for NH₃ from these data.
69. Determine whether aqueous solutions of the following salts are acidic, basic, or neutral:
    1. Al(NO₃)₃
    2. RbI
    3. KHCO₂
    4. CH₃NH₃Br
70. Determine whether aqueous solutions of the following salts are acidic, basic, or neutral:
    1. FeCl₃
    2. K₂CO₃
    3. NH₄Br
    4. KClO₄
71. Novocaine, C₁₃H₂₁O₂N₂Cl, is the salt of the base procaine and hydrochloric acid. The ionization constant for procaine is 7 × 10⁻⁶. Is a solution of novocaine acidic or basic? What are [H₃O⁺], [OH⁻], and pH of a 2.0% solution by mass of novocaine, assuming that the density of the solution is 1.0 g/mL.
72. Which of the following concentrations would be practically equal in a calculation of the equilibrium concentrations in a 0.134-M solution of H₂CO₃, a diprotic acid: [H₃O⁺], [OH⁻], [H₂CO₃], [HCO₃ ⁻], [CO₃ ²⁻]? No calculations are needed to answer this question.
73. Calculate the concentration of each species present in a 0.050-M solution of H₂S.
74. Calculate the concentration of each species present in a 0.010-M solution of phthalic acid,C₆H₄(CO₂H)₂.C₆H₄(CO₂H)₂(aq) + H₂O(l) ⇌  H₃O⁺(aq)+C₆H₄(CO₂H)(CO₂)^–(aq)           K_a=1.1 x 10^-3
    C₆H₄(CO₂H)(CO₂)(aq) + H₂O(l) ⇌ H₃O^+(aq) + C₆H₄(CO₂)₂ ^2-(aq)                                  K_a= 3.9 x 10^-6
75. Salicylic acid, HOC₆H₄CO₂H, and its derivatives have been used as pain relievers for a long time. Salicylic acid occurs in small amounts in the leaves, bark, and roots of some vegetation (most notably historically in the bark of the willow tree). Extracts of these plants have been used as medications for centuries. The acid was first isolated in the laboratory in 1838.
    1. Both functional groups of salicylic acid ionize in water, with K_a = 1.0 × 10⁻³ for the—CO₂H group and 4.2 × 10⁻¹³ for the −OH group. What is the pH of a saturated solution of the acid (solubility = 1.8 g/L).
    2. Aspirin was discovered as a result of efforts to produce a derivative of salicylic acid that would not be irritating to the stomach lining. Aspirin is acetylsalicylic acid, CH₃CO₂C₆H₄CO₂H. The −CO₂H functional group is still present, but its acidity is reduced, K_a = 3.0 × 10⁻⁴. What is the pH of a solution of aspirin with the same concentration as a saturated solution of salicylic acid (See Part a).
76. The ion HTe⁻ is an amphiprotic species; it can act as either an acid or a base.
    1. What is K_a for the acid reaction of HTe⁻ with H₂O?
    2. What is K_b for the reaction in which HTe⁻ functions as a base in water?
    3. Demonstrate whether or not the second ionization of H₂Te can be neglected in the calculation of [HTe⁻] in a 0.10 M solution of H₂Te.
77. Explain why a buffer can be prepared from a mixture of NH₄Cl and NaOH but not from NH₃ and NaOH.
78. Explain why the pH does not change significantly when a small amount of an acid or a base is added to a solution that contains equal amounts of the acid H₃PO₄ and a salt of its conjugate base NaH₂PO₄.
79. Explain why the pH does not change significantly when a small amount of an acid or a base is added to a solution that contains equal amounts of the base NH₃ and a salt of its conjugate acid NH₄Cl.
80. What is [H₃O+] in a solution of 0.25 M CH₃CO₂H and 0.030 M NaCH₃CO₂?
    CH₃CO₂H(aq) + H₂O(l) ⇌ H₃O⁺(aq) + CH₃CO₂ ⁻(aq)      Ka = 1.8 × 10⁻⁵
81. What is [H₃O+] in a solution of 0.075 M HNO₂ and 0.030 M NaNO₂?HNO2(aq) + H2 O(l) ⇌ H3 O+(aq) + NO2 −(aq)Ka = 4.5 × 10−5
82. What is [OH−] in a solution of 0.125 M CH₃NH₂ and 0.130 M CH₃NH₃Cl?
    CH3 NH2(aq) + H2 O(l) ⇌ CH3 NH3 +(aq) + OH−(aq)Kb = 4.4 × 10−4
83. What is [OH−] in a solution of 1.25 M NH₃ and 0.78 M NH₄NO₃? NH3(aq) + H2 O(l) ⇌ NH4 +(aq) + OH−(aq)Kb = 1.8 × 10−5
84. What is the effect on the concentration of acetic acid, hydronium ion, and acetate ion when the following are added to an acidic buffer solution of equal concentrations of acetic acid and sodium acetate:
    1. HCl
    2. KCH₃CO₂
    3. NaCl
    4. KOH
    5. CH₃CO₂H
85. What is the effect on the concentration of ammonia, hydroxide ion, and ammonium ion when the following are added to a basic buffer solution of equal concentrations of ammonia and ammonium nitrate:
    1. KI
    2. NH₃
    3. HI
    4. NaOH
    5. NH₄Cl
86. What will be the pH of a buffer solution prepared from 0.20 mol NH₃, 0.40 mol NH₄NO₃, and just enough water to give 1.00 L of solution?
87. Calculate the pH of a buffer solution prepared from 0.155 mol of phosphoric acid, 0.250 mole of KH₂PO₄, and enough water to make 0.500 L of solution.
88. How much solid NaCH₃CO₂•3H₂O must be added to 0.300 L of a 0.50-M acetic acid solution to give a buffer with a pH of 5.00? (Hint: Assume a negligible change in volume as the solid is added.)
89. What mass of NH₄Cl must be added to 0.750 L of a 0.100-M solution of NH₃ to give a buffer solution with a pH of 9.26? (Hint: Assume a negligible change in volume as the solid is added.)
90. A buffer solution is prepared from equal volumes of 0.200 M acetic acid and 0.600 M sodium acetate. Use 1.80 × 10⁻⁵ as K_a for acetic acid.
    1. What is the pH of the solution?
    2. Is the solution acidic or basic?
    3. What is the pH of a solution that results when 3.00 mL of 0.034 M HCl is added to 0.200 L of the original buffer?
91. A 5.36–g sample of NH₄Cl was added to 25.0 mL of 1.00 M NaOH and the resulting solution diluted to 0.100 L.
    1. What is the pH of this buffer solution?
    2. Is the solution acidic or basic?
    3. What is the pH of a solution that results when 3.00 mL of 0.034 M HCl is added to the solution?
92. Explain how to choose the appropriate acid-base indicator for the titration of a weak base with a strong acid.
93. Explain why an acid-base indicator changes color over a range of pH values rather than at a specific pH.
94. Calculate the pH at the following points in a titration of 40 mL (0.040 L) of 0.100 M barbituric acid (K_a = 9.8 × 10⁻⁵) with 0.100 M KOH.
    1. no KOH added
    2. 20 mL of KOH solution added
    3. 39 mL of KOH solution added
    4. 40 mL of KOH solution added
    5. 41 mL of KOH solution added
95. The indicator dinitrophenol is an acid with a K_a of 1.1 × 10⁻⁴. In a 1.0 × 10⁻⁴–M solution, it is colorless in acid and yellow in base. Calculate the pH range over which it goes from 10% ionized (colorless) to 90% ionized (yellow).