Private: Chapter Fourteen
Polyprotic Acids (14.5)
OpenStax
Learning Objectives
By the end of this section, you will be able to:
- Extend previously introduced equilibrium concepts to acids and bases that may donate or accept more than one proton
Acids are classified by the number of protons per molecule that they can give up in a reaction. Acids such as HCl, HNO3, and HCN that contain one ionizable hydrogen atom in each molecule are called monoprotic acids. Their reactions with water are:
HCl(aq) + H2O(l) ⟶ H3O+(aq) + Cl−(aq)
HNO3(aq) + H2O(l) ⟶ H3O+(aq) + NO3 −(aq)
HCN(aq) + H2O(l) ⇌ H3O+(aq) + CN−(aq)
Even though it contains four hydrogen atoms, acetic acid, CH3CO2H, is also monoprotic because only the hydrogen atom from the carboxyl group (COOH) reacts with bases:
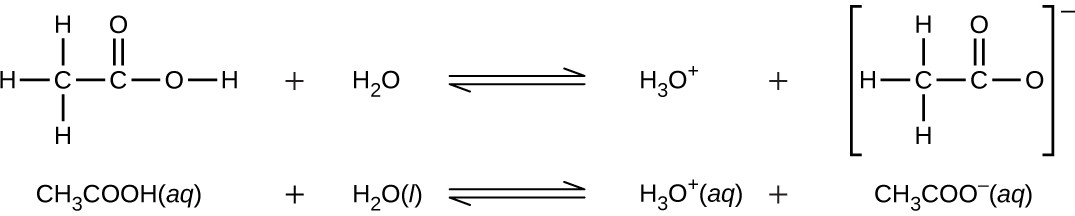
Similarly, monoprotic bases are bases that will accept a single proton.
Diprotic acids contain two ionizable hydrogen atoms per molecule; ionization of such acids occurs in two steps. The first ionization always takes place to a greater extent than the second ionization. For example, sulfuric acid, a strong acid, ionizes as follows:
First ionization: H2SO4(aq) + H2O(l) ⇌ H3O+(aq) + HSO4 −(aq)
Ka1 = more than 102 ; complete dissociation
Second ionization: HSO4 −(aq) + H2O(l) ⇌ H3O+(aq) + SO4 2−(aq)
Ka2 = 1.2 × 10−2
This stepwise ionization process occurs for all polyprotic acids. Carbonic acid, H2CO3, is an example of a weak diprotic acid. The first ionization of carbonic acid yields hydronium ions and bicarbonate ions in small amounts.
First ionization:
H2CO3(aq) + H2O(l) ⇌ H3O+(aq) + HCO3−(aq)
[latex]K_{H_{2}CO_{3}} = \frac{[H_{3}O^{+}][HCO_{3} ^{-}]}{[H_{2}CO_{3}]} = 4.3 \times 10^{-7}[/latex]
The bicarbonate ion can also act as an acid. It ionizes and forms hydronium ions and carbonate ions in even smaller quantities.
Second ionization:
HCO3 −(aq) + H2O(l) ⇌ H3O+(aq) + CO3 2−(aq)
[latex]K_{HCO_{3} ^{-}} = \frac{[H_{3}O^{+}][HCO_{3} ^{-}]}{[HCO_{3} ^{-}]} = 4.3 \times 10^{-7}[/latex]
KH2CO3 is larger than KHCO3− by a factor of 104, so H2CO3 is the dominant producer of hydronium ion in the solution. This means that little of the HCO3− formed by the ionization of H2CO3 ionizes to give hydronium ions (and carbonate ions), and the concentrations of H3O+ and HCO3 − are practically equal in a pure aqueous solution of H2CO3.
If the first ionization constant of a weak diprotic acid is larger than the second by a factor of at least 20, it is appropriate to treat the first ionization separately and calculate concentrations resulting from it before calculating concentrations of species resulting from subsequent ionization. This approach is demonstrated in the following example exercise.
Example 14.19
Ionization of a Diprotic Acid
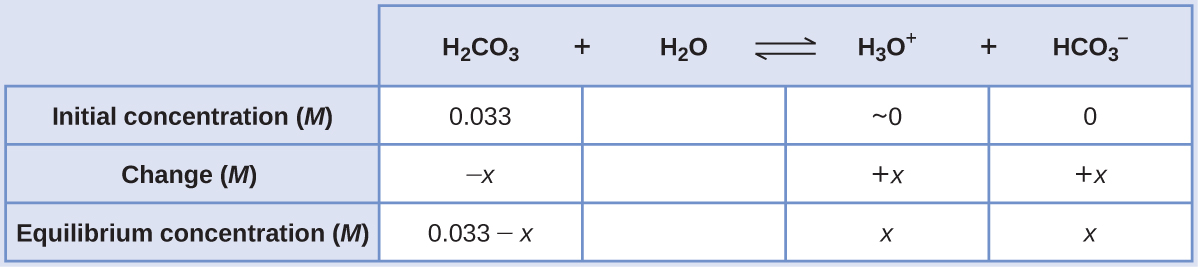
“Carbonated water” contains a palatable amount of dissolved carbon dioxide. The solution is acidic because CO2 reacts with water to form carbonic acid, H2CO3. What are [H3O+],saturated solution of CO2 with an initial [H2CO3] = 0.033 M?
Solution
As indicated by the ionization constants, H2CO3 is a much stronger acid than HCO3 −, so the stepwise ionization reactions may be treated separately.
The first ionization reaction is:
H2CO3(aq) + H2O(l) ⇌ H3O+(aq) + HCO3 −(aq) Ka1 = 4.3 × 10−7
Using provided information, an ICE table for this first step is prepared:
Substituting the equilibrium concentrations into the equilibrium equation gives
[latex]K_{H_{2}CO_{3}} = \frac{[H_{3}O^{+}][HCO_{3} ^{-}]}{[H_{2}CO_{3}]} = \frac{(x)(x)}{0.033 - x} = 4.3 \times 10^{-7}[/latex]
Assuming x << 0.033 and solving the simplified equation yields
x = 1.2 × 10−4
The ICE table defined x as equal to the bicarbonate ion molarity and the hydronium ion molarity:
[H2CO3] = 0.033 M
[H3O+] = [HCO3 −] = 1.2 × 10−4 M
Using the bicarbonate ion concentration computed above, the second ionization is subjected to a similar equilibrium calculation:
HCO3 −(aq) + H2O(l) ⇌ H3O+(aq) + CO3 2−(aq)
[latex]K_{HCO_{3}}^{-} = \frac{[H_{3}O^{+}][CO_{3} ^{2-}]}{[HCO_{3} ^{-}]} = \frac{(1.2 \times 10^{-4})[CO_{3} ^{2-}]}{1.2 \times 10^{-4}}[/latex]
[latex][CO_{3} ^{2-}] = \frac{(4.7 \times 10^{-11})(1.2 \times 10^{-4})}{1.2 \times 10^{-4}}[/latex] = 4.7 x 10-11 M
To summarize: at equilibrium [H2CO3] = 0.033 M; [H3O+] = 1.2 × 10−4; [HCO3 −] = 1.2 × 10−4 M; [CO3 2−] = 5.6 × 10−11 M.
Check Your Learning
The concentration of H2S in a saturated aqueous solution at room temperature is approximately 0.1 M. Calculate [H3O+], [HS−], and [S2−] in the solution:
H2S(aq) + H2O(l) ⇌ H3O+(aq) + HS−(aq) Ka1 = 8.9 × 10−8
HS−(aq) + H2O(l) ⇌ H3O+(aq) + S2−(aq) Ka2 = 1.0 × 10−19
Answer: [H2S] = 0.1 M; [H3O+] = [HS−] = 0.000094 M; [S2−] = 1 × 10−19 M
A triprotic acid is an acid that has three ionizable H atoms. Phosphoric acid is one example:
First ionization: H3PO4(aq) + H2O(l) ⇌ H3O+(aq) + H2PO4 −(aq)
Ka1 = 7.5 × 10−3
Second ionization: H2PO4 −(aq) + H2O(l) ⇌ H3O+(aq) + HPO4 2−(aq)
Ka2 = 6.2 × 10−8
Third ionization: HPO4 2−(aq) + H2O(l) ⇌ H3O+(aq) + PO4 3−(aq)
Ka3 = 4.2 × 10−13
As for the diprotic acid examples, each successive ionization reaction is less extensive than the former, reflected in decreasing values for the stepwise acid ionization constants. This is a general characteristic of polyprotic acids and successive ionization constants often differ by a factor of about 105 to 106.
This set of three dissociation reactions may appear to make calculations of equilibrium concentrations in a solution of H3PO4 complicated. However, because the successive ionization constants differ by a factor of 105 to 106, large differences exist in the small changes in concentration accompanying the ionization reactions. This allows the use of math-simplifying assumptions and processes, as demonstrated in the examples above.
Polyprotic bases are capable of accepting more than one hydrogen ion. The carbonate ion is an example of a diprotic base, because it can accept two protons, as shown below. Similar to the case for polyprotic acids, note the ionization constants decrease with ionization step. Likewise, equilibrium calculations involving polyprotic bases follow the same approaches as those for polyprotic acids.
H2O(l) + CO3 2−(aq) ⇌ HCO3 −(aq) + OH−(aq) Kb1 = 2.1 × 10−4
H2O(l) + HCO3 − (aq) ⇌ H2CO3(aq) + OH− (aq) Kb2 = 2.3 × 10−8