Valence Bond Theory (5.1)

Valence Bond Theory

By the end of this section, you will be able to:

• Describe the formation of covalent bonds in terms of atomic orbital overlap
• Define and give examples of σ and π bonds

As we know, a scientific theory is a strongly supported explanation for observed natural laws or large bodies of experimental data. For a theory to be accepted, it must explain experimental data and be able to predict behavior. For example, VSEPR theory has gained widespread acceptance because it predicts three-dimensional molecular shapes that are consistent with experimental data collected for thousands of different molecules. However, VSEPR theory does not provide an explanation of chemical bonding.

Atomic Orbital Overlap

There are successful theories that describe the electronic structure of atoms. We can use quantum mechanics to predict the specific regions around an atom where electrons are likely to be located: A spherical shape for an s orbital, a dumbbell shape for a p orbital, and so forth. However, these predictions only describe the orbitals around free atoms. When atoms bond to form molecules, atomic orbitals are not sufficient to describe the regions where electrons will be located in the molecule. A more complete understanding of electron distributions requires a model that can account for the electronic structure of molecules. One popular theory holds that a covalent bond forms when a pair of electrons is shared by two atoms and is simultaneously attracted by the nuclei of both atoms. In the following sections, we will discuss how such bonds are described by valence bond theory and hybridization.

Valence bond theory describes a covalent bond as the overlap of half-filled atomic orbitals (each containing a single electron) that yield a pair of electrons shared between the two bonded atoms. We say that orbitals on two different atoms overlap when a portion of one orbital and a portion of a second orbital occupy the same region of space. According to valence bond theory, a covalent bond results when two conditions are met: (1) an orbital on one atom overlaps an orbital on a second atom and (2) the single electrons in each orbital combine to form an electron pair. The mutual attraction between this negatively charged electron pair and the two atoms’ positively charged nuclei serves to physically link the two atoms through a force we define as a covalent bond. The strength of a covalent bond depends on the extent of overlap of the orbitals involved. Orbitals that overlap extensively form bonds that are stronger than those that have less overlap.

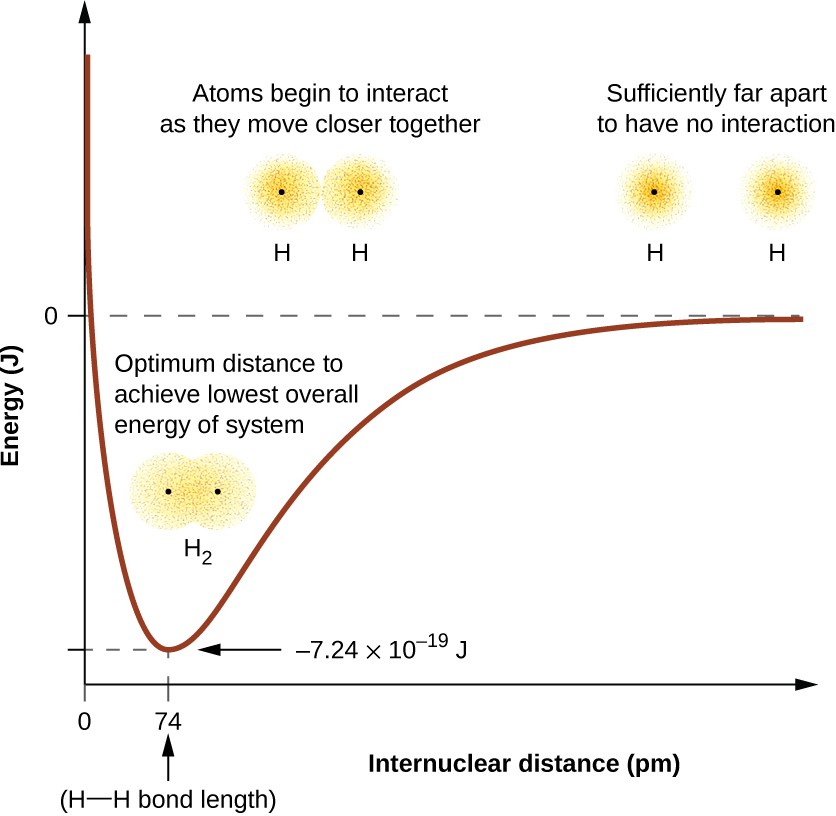
The energy of the system depends on how much the orbitals overlap. Figure 5.3 illustrates how the sum of the energies of two hydrogen atoms (the colored curve) changes as they approach each other. When the atoms are far apart there is no overlap, and by convention we set the sum of the energies at zero. As the atoms move together, their orbitals begin to overlap. Each electron begins to feel the attraction of the nucleus in the other atom. In addition, the electrons begin to repel each other, as do the nuclei. While the atoms are still widely separated, the attractions are slightly stronger than the repulsions, and the energy of the system decreases. (A bond begins to form.) As the atoms move closer together, the overlap increases, so the attraction of the nuclei for the electrons continues to increase (as do the repulsions among electrons and between the nuclei). At some specific distance between the atoms, which varies depending on the atoms involved, the energy reaches its lowest (most stable) value. This optimum distance between the two bonded nuclei is the bond distance between the two atoms. The bond is stable because at this point, the attractive and repulsive forces combine to create the lowest possible energy configuration. If the distance between the nuclei were to decrease further, the repulsions between nuclei and the repulsions as electrons are confined in closer proximity to each other would become stronger than the attractive forces. The energy of the system would then rise (making the system destabilized), as shown at the far left of Figure 5.3.

In addition to the distance between two orbitals, the orientation of orbitals also affects their overlap (other than for two s orbitals, which are spherically symmetric). Greater overlap is possible when orbitals are oriented such that they overlap on a direct line between the two nuclei. Figure 5.4 illustrates this for two p orbitals from different atoms; the overlap is greater when the orbitals overlap end to end rather than at an angle.

The overlap of two s orbitals (as in H₂), the overlap of an s orbital and a p orbital (as in HCl), and the end-to-end overlap of two p orbitals (as in Cl₂) all produce sigma bonds (σ bonds), as illustrated in Figure 5.5. A σ bond is a covalent bond in which the electron density is concentrated in the region along the internuclear axis; that is, a line between the nuclei would pass through the center of the overlap region. Single bonds in Lewis structures are described as σ bonds in valence bond theory.

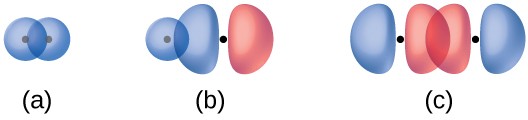
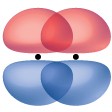
A pi bond (π bond) is a type of covalent bond that results from the side-by-side overlap of two p orbitals, as illustrated in Figure 5.6. In a π bond, the regions of orbital overlap lie on opposite sides of the internuclear axis. Along the axis itself, there is a node, that is, a plane with no probability of finding an electron.

While all single bonds are σ bonds, multiple bonds consist of both σ and π bonds. As the Lewis structures below suggest, O₂ contains a double bond, and N₂ contains a triple bond. The double bond consists of one σ bond and one π bond, and the triple bond consists of one σ bond and two π bonds. Between any two atoms, the first bond formed will always be a σ bond, but there can only be one σ bond in any one location. In any multiple bond, there will be one σ bond, and the remaining one or two bonds will be π bonds. These bonds are described in more detail later in this chapter.

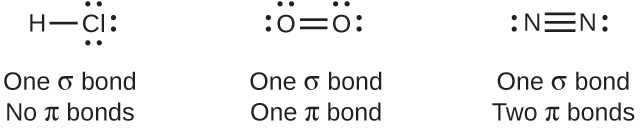
Example 5.1

Counting σ and π Bonds

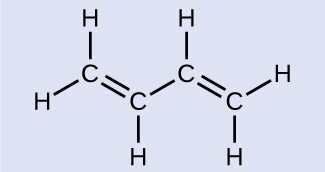
Butadiene, C4H6, is used to make synthetic rubber. Identify the number of σ and π bonds contained in this molecule.

Solution

There are six σ C–H bonds and one σ C–C bond, for a total of seven from the single bonds. There are two double bonds that each have a π bond in addition to the σ bond. This gives a total nine σ and two π bonds overall.

Check Your Learning

Identify each illustration as depicting a σ or π bond:side-by-side overlap of a 4p and a 2p orbitalend-to-end overlap of a 4p and 4p orbitalend-to-end overlap of a 4p and a 2p orbital

Answer: (a) is a π bond with a node along the axis connecting the nuclei while (b) and (c) are σ bonds thatoverlap along the axis.

Dipole Moments and Ionic Character

Now that we have seen the importance of understanding the connection between the location of electrons in atoms and the properties of elements, we can expand our understanding of the connection between atoms. This will be an introduction to more advanced aspects of the chemical bond, which is the very heart of chemistry itself. With the sole exception of the noble gases, atoms by themselves do not possess the most stable possible electron configuration. That is where the concept of chemical bonding comes into its own: atoms can attain a stable configuration by exchanging electrons with another atom, resulting in the formation of ions.

Ions, in turn, can associate by charge – simple Coulombic attraction – resulting in the formation of compounds we call ionic compounds. We will look at the ionic nature of bonds first, from a simple positive-negative attraction standpoint. Just as important is that some atoms bond by sharing rather than exchanging electrons; the sharing of electrons gives rise to the covalent bond. To add just one more dimension, some chemical species are neither completely ionic nor completely covalent; these species possess a permanent dipole, and are classified as polar.

In your introductory physics course, you will likely discuss the concept of Coulombic interactions in much more rigorous detail than we will do here. We are interested primarily in the differences in properties between species that arise from their relative covalent, ionic, or polar nature – not in a rigorous model of those properties. We are concerned with the connection between potential energy and force and the relative separation (or lack of separation) between charges. We begin by defining the electric or Coulomb force as the product of the charges divided by the square of the distance between those charges:

F = [latex]\frac{Q_{1}Q_{2}}{d^{2}}[/latex]

Here, Q is taken to be the fundamental constant of electron charge: one electron has a charge of 1.60218×10−19 C . (We will work exclusively in the SI system, so distances will be measured in meters (m)).

And as you may recall, energy is force times distance, so

E = [latex]\frac{Q_{1}Q_{2}}{d}[/latex]

To illustrate the trend in attractive force, we will consider first the attractive force between two ions of single charge separated by a distance of 2d:

[latex]F=\frac{(1)(-1)}{(2 d)^{2}}=-\frac{1}{4 d^{2}}[/latex]

And then the attractive force between two ions of double charge separated by a distance d:

[latex]F=\frac{(2)(-2)}{(d)^{2}}=-\frac{4}{d^{2}}[/latex]

The force of attraction increases with the charge and decreases with increased distance. If all matter were composed of ions that would be the end of the story, but it clearly is not. There are molecules for which the charge – either positive or negative – is permanently concentrated more on one atom than the other. Notice we say atom, because these compounds are not composed of ions but rather of atoms sharing electrons through covalent bonds.

Bond Dipole Moments

The concept of a bond dipole moment allows us to examine the partial separation of charge between atoms. It is a simple model when applied to diatomic molecules, which will be more than sufficient for our purposes. The dipole moment of a bond is defined as the charge times the distance – charge once again being measured in multiples of the charge on an electron, or coulombs. The distance will always be in meters. Because we are considering very small charges and distances, and because it is the relative separation of charge rather than the actual value for it that we are interested in, we will introduce a new unit called the Debye, named after the physical chemist Peter Debye:

1 Debye (D) = 3.336×10⁻³⁰ C-m                     μ = Q×d

The usefulness of the Debye unit will be shown by example:

For HCl, the bond dipole moment is known to be 1.08 D For HI, the bond dipole moment is known to be 0.44 D

Comparing the two, we can see that HI is less polar than HCl, which is what we would expect based on electronegativity values.

We have now made a transition between the concept of an ionic compound and a partially ionic one. Of course, the partially ionic compound must also by definition be partially covalent.

Partial Ionic Character

The concept of the bond dipole moment helps bridge the concepts of ionic and covalent bonding. Because there is a separation of charge that is less complete than it is in an ionic bond, we can refer to polar bonds as being partially ionic in nature. In contrast to sodium chloride, hydrogen chloride shows partial charges (indicated with a delta notation) on the hydrogen and chlorine. As you would expect from the electronegativity values, hydrogen carries a partial positive charge, while chlorine carries a partial negative charge. Where do these charges come from?

It is easy to come up with the partial charges by comparing the actual dipole moments (which can be obtained experimentally, using spectroscopy) with the dipole expected in the limiting case (that is, if we were to consider the molecule ionic). The actual dipole moment is 1.03 D.

Check Your Learning

Repeat the calculation for HI, which has a dipole moment of 0.42 D and a bond length of 0.161 nm.

Answer:

Calculated 7.73, percent 5.43

What does the result suggest about the relative polarity of the HI bond vs. that of the HCl bond? Does the calculated dipole and percent ionic character reconcile with the difference in electronegativity between Cl and I?

The electron configuration of an atom or ion is key to understanding the chemical behavior of an element. The atoms that make up the element combine in various ways, ranging from the mostly ionic (NaCl) to the partially ionic (HCl) to what we will call purely covalent. At the most fundamental level, all chemical bonds involve electrons, and a significant percentage of chemical and physical properties can be explained by considering the location and separation of charge in a species. By understanding the structure of matter at the atomic level, we can begin to build an understanding of the behavior of matter at both the microscopic and macroscopic levels.

An understanding of dipoles and partial ionic character is fundamental to understanding the interactions between particles, which we will examine in the chapter on liquids and solids. These intermolecular forces become important in the liquid and solid states of matter.