3.1 Rules of Differentiation
Derivatives of Formulas
In the next few sections, we’ll consider the derivative rules that will let us find formulas for derivatives when our function comes to us as a formula. This is a very algebraic section, and you should get lots of practice. When you tell someone you have studied calculus, this is the one skill they will expect you to have.
Building Blocks
These are the simplest rules – rules for the basic functions. We won’t prove these rules; we’ll just use them. But first, let’s look at a few so that we can see they make sense.
Example 1
Find the derivative of [latex]y=f(x)=mx+b[/latex]
This is a linear function, so its graph is its own tangent line! The slope of the tangent line, the derivative, is the slope of the line: \[f'(x)=m\]
Rule:
The derivative of a linear function is its slope.
Example 2
Find the derivative of [latex]f(x)=135[/latex].
Think about this one graphically, too. The graph of f(x) is a horizontal line. So its slope is zero: \[f'(x)=0\]
Rule:
The derivative of a constant is zero.
Example 3
Find the derivative of [latex]f(x)=x^2[/latex].
Recall the formal definition of the derivative: \[f'(x)=\lim\limits_{h\to 0} \frac{f(x+h)-f(x)}{h}.\]
Using our function [latex]f(x)=x^2[/latex], [latex]f(x+h)=(x+h)^2=x^2+2xh+h^2[/latex].
Then
\[ \begin{align*}
f'(x)=& \lim\limits_{h\to 0} \frac{f(x+h)-f(x)}{h}\\
=& \lim\limits_{h\to 0} \frac{x^2+2xh+h^2-x^2}{h}\\
=& \lim\limits_{h\to 0} \frac{2xh+h^2}{h}\\
=& \lim\limits_{h\to 0} \frac{h(2x+h)}{h}\\
=& \lim\limits_{h\to 0} (2x+h)\\
=& 2x
\end{align*} \]
From all that, we find that [latex]f'(x)=2x[/latex].
Luckily, there is a handy rule we use to skip using the limit:
Power Rule
The derivative of [latex]f(x)=x^n[/latex] is \[f'(x)=nx^{n-1}.\]
Example 4
Find the derivative of [latex]g(x)=4x^3[/latex]
Using the power rule, we know that if [latex]f(x)=x^3[/latex], then [latex]f'(x)=3x^2[/latex]. Notice that [latex]g[/latex] is 4 times the function [latex]f[/latex]. Think about what this change means to the graph of [latex]g[/latex] – it’s now 4 times as tall as the graph of [latex]f[/latex]. If we find the slope of a secant line, it will be [latex]\frac{\Delta g}{\Delta x}= \frac{4\Delta f}{\Delta x} =4\frac{\Delta f}{\Delta x}[/latex]; each slope will be 4 times the slope of the secant line on the [latex]f[/latex] graph. This property will hold for the slopes of tangent lines, too: \[\frac{d}{dx}\left(4x^3\right)=4\frac{d}{dx}\left(x^3\right)=4\cdot 3x^2=12x^2.\]
Rule:
Constants come along for the ride, i.e., [latex]\frac{d}{dx}\left( kf\right)=kf'.[/latex]
Here are all the basic rules in one place.
Derivative Rules: Building Blocks
In what follows, [latex]f[/latex] and [latex]g[/latex] are differentiable functions of [latex]x[/latex].
Constant Multiple Rule
\[ \frac{d}{dx}\left( kf\right)=kf’\]
Sum and Difference Rule
\[\frac{d}{dx}\left(f\pm g\right)=f’ \pm g’\]
Power Rule
\[\frac{d}{dx}\left(x^n\right)=nx^{n-1}\]
Special cases:
\[\frac{d}{dx}\left(k\right)=0 \quad \text{Because} \;k=kx^0.\]
\[\frac{d}{dx}\left(x\right)=1 \quad \text{Because} \;x=x^1.\]
Exponential Functions
\[\frac{d}{dx}\left(e^x\right)=e^x\] \[\frac{d}{dx}\left(a^x\right)=\ln(a)\,a^x\]
Natural Logarithm
\[\frac{d}{dx}\left(\ln(x)\right)=\frac{1}{x}\]
The sum, difference, and constant multiple rule combined with the power rule allow us to easily find the derivative of any polynomial.
Example 5
Find the derivative of [latex]p(x)=17x^{10}+13x^8-1.8x+1003[/latex].
[latex]\frac{d}{dx}\left( 17x^{10}+13x^8-1.8x+1003 \right)=[/latex]
\[ \begin{align*}=& \frac{d}{dx}\left( 17x^{10} \right)+\frac{d}{dx}\left( 13x^8 \right)-\frac{d}{dx}\left( 1.8x \right)+\frac{d}{dx}\left( 1003 \right)\\
=& 17\frac{d}{dx}\left( x^{10} \right)+13\frac{d}{dx}\left( x^8 \right)-1.8\frac{d}{dx}\left( x \right)+\frac{d}{dx}\left( 1003 \right)\\
=& 17\left(10x^9\right)+13\left(8x^7\right)-1.8\left(1\right)+0\\
=& 170x^9+104x^7-1.8
\end{align*} \]
You don’t have to show every single step. Do be careful when you’re first working with the rules, but pretty soon you’ll be able to just write down the derivative directly:
Example 6
Find [latex]\frac{d}{dx}\left( 17x^2-33x+12 \right)[/latex].
Writing out the rules, we’d write \[\frac{d}{dx}\left( 17x^2-33x+12 \right)=17(2x)-33(1)+0=34x-33.\]
Once you’re familiar with the rules, you can, in your head, multiply the 2 times the 17 and the 33 times 1, and just write \[\frac{d}{dx}\left( 17x^2-33x+12 \right)=34x-33.\]
The power rule works even if the power is negative or a fraction. In order to apply it, first translate all roots and basic rational expressions into exponents:
Example 7
Find the derivative of [latex]y=3\sqrt{t}-\frac{4}{t^4}+5e^t[/latex].
The first step is translate into exponents: \[y=3\sqrt{t}-\frac{4}{t^4}+5e^t=3t^{1/2}-4t^{-4}+5e^t\]
Now you can take the derivative:
\[ \begin{align*}
\frac{d}{dt}\left( 3t^{1/2}-4t^{-4}+5e^t \right)=& 3\left(\frac{1}{2}t^{-1/2}\right)-4\left(-4t^{-5}\right)+5\left(e^t\right) \\
=& \frac{3}{2}t^{-1/2}+16t^{-5}+5e^t
\end{align*} \]
If there is a reason to, you can rewrite the answer with radicals and positive exponents: \[y’= \frac{3}{2}t^{-1/2}+16t^{-5}+5e^t= \frac{3}{2\sqrt{t}}+\frac{16}{t^5}+5e^t\]
Be careful when finding the derivatives with negative exponents.
We can immediately apply these rules to solve the problem we started the chapter with – finding a tangent line.
Example 8
Find the equation of the line tangent to [latex]g(t)=10-t^2[/latex] when [latex]t = 2[/latex].
The slope of the tangent line is the value of the derivative. We can compute [latex]g'(t)=-2t[/latex]. To find the slope of the tangent line when [latex]t = 2[/latex], evaluate the derivative at that point. The slope of the tangent line is -4.
To find the equation of the tangent line, we also need a point on the tangent line. Since the tangent line touches the original function at [latex]t = 2[/latex], we can find the point by evaluating the original function: [latex]g(2)=10-2^2=6[/latex]. The tangent line must pass through the point (2, 6).
Using the point-slope equation of a line, the tangent line will have equation [latex]y-6=-4(t-2)[/latex]. Simplifying to slope-intercept form, the equation is [latex]y=-4t+14[/latex].
Graphing, we can verify this line is indeed tangent to the curve:
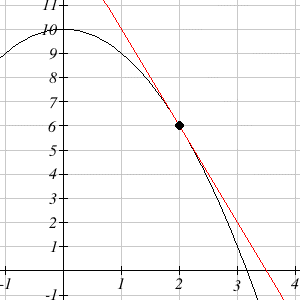
Long description: A tangent line is shown passing through the point (2, 6). The x-axis extends from -1 to 4 and the y-axis extends from -1 to 11.
We can also use these rules to help us find the derivatives we need to interpret the behavior of a function.
Example 9
In a memory experiment, a researcher asks the subject to memorize as many words from a list as possible in 10 seconds. Recall is tested, then the subject is given 10 more seconds to study, and so on. Suppose the number of words remembered after [latex]t[/latex] seconds of studying could be modeled by [latex]W(t)=4t^{2/5}[/latex]. Find and interpret [latex]W'(20)[/latex].
[latex]W'(t)=4\cdot \frac{2}{5}t^{-3/5}=\frac{8}{5}t^{-3/5}[/latex], so [latex]W'(20)=\frac{8}{5}(20)^{-3/5}\approx 0.2652[/latex].
Since [latex]W[/latex] is measured in words, and [latex]t[/latex] is in seconds, [latex]W'[/latex] has units words per second. [latex]W'(20)\approx 0.2652[/latex] means that after 20 seconds of studying, the subject is learning about 0.27 more words for each additional second of studying.

