2.5 One Sided Limits and Continuity
One-Sided Limits
Sometimes indicating that the limit of a function fails to exist at a point does not provide us with enough information about the behavior of the function at that particular point. To see this, we now consider the function [latex]g(x)=|x−2|/(x−2)[/latex]. As we pick values of x close to 2, [latex]g(x)[/latex] does not approach a single value, so the limit as x approaches 2 does not exist—that is, [latex]\displaystyle \lim_{x\rightarrow 2}g(x)[/latex] DNE. However, this statement alone does not give us a complete picture of the behavior of the function around the x-value 2. To provide a more accurate description, we introduce the idea of a one-sided limit. For all values to the left of 2 (or the negative side of 2), [latex]𝑔(𝑥)=−1[/latex]. Thus, as x approaches 2 from the left, [latex]𝑔(𝑥)[/latex] approaches −1. Mathematically, we say that the limit as x approaches 2 from the left is −1. Symbolically, we express this idea as
$$\displaystyle \lim_{𝑥\rightarrow 2^-}𝑔(𝑥)=-1.$$
Similarly, as x approaches 2 from the right (or from the positive side), [latex]𝑔(𝑥)[/latex] approaches 1. Symbolically, we express this idea as
$$\displaystyle \lim_{𝑥\rightarrow 2^+}𝑔(𝑥)=1.$$
We can now present an informal definition of one-sided limits.
DEFINITION
We define two types of one-sided limits.
Limit from the left: Let [latex]𝑓(𝑥)[/latex] be a function defined at all values in an open interval of the form [latex](c, a)[/latex], and let [latex]L[/latex] be a real number. If the values of the function [latex]𝑓(𝑥)[/latex] approach the real number [latex]L[/latex] as the values of [latex]x[/latex] (where [latex]𝑥<𝑎[/latex]) approach the number [latex]a[/latex], then we say that L is the limit of [latex]𝑓(𝑥)[/latex] as [latex]x[/latex] approaches a from the left. Symbolically, we express this idea as $$\displaystyle\lim_{𝑥\rightarrow 𝑎^−}𝑓(𝑥)=𝐿.$$ 2.6 Limit from the right: Let [latex]𝑓(𝑥)[/latex] be a function defined at all values in an open interval of the form [latex](𝑎,𝑐)[/latex], and let [latex]L[/latex] be a real number. If the values of the function [latex]𝑓(𝑥)[/latex] approach the real number [latex]L[/latex] as the values of [latex]x[/latex] (where [latex]𝑥>𝑎[/latex]) approach the number [latex]a[/latex], then we say that [latex]L[/latex] is the limit of [latex]𝑓(𝑥)[/latex] as [latex]x[/latex] approaches [latex]a[/latex] from the right. Symbolically, we express this idea as
$$\displaystyle\lim_{𝑥\rightarrow 𝑎^+}𝑓(𝑥)=𝐿.$$
Example 1
Evaluate the one sided limits of the function [latex]f(x)[/latex] graphed below at [latex]x = 0[/latex] and [latex]x = 1[/latex].
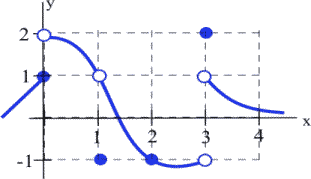
As [latex]x[/latex] approach 0 from the left, the value of the function is getting closer to 1, so [latex]\lim\limits_{x\to 0^-} f(x) = 1.[/latex]
As [latex]x[/latex] approaches 0 from the right, the value of the function is getting closer to 2, so [latex]\lim\limits_{x\to 0^+} f(x) = 2.[/latex]
Notice that since the limit from the left and limit from the right are different, the general limit, [latex]\lim\limits_{x\to 0} f(x)[/latex], does not exit.
At [latex]x[/latex] approaches 1 from either direction, the value of the function is approaching 1, so \[\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^+} f(x) = \lim\limits_{x\to 1} f(x) = 1. \]
Let us now consider the relationship between the limit of a function at a point and the limits from the right and left at that point. It seems clear that if the limit from the right and the limit from the left have a common value, then that common value is the limit of the function at that point. Similarly, if the limit from the left and the limit from the right take on different values, the limit of the function does not exist. These conclusions are summarized in the following theorem.
Relating One-Sided and Two-Sided Limits
Let [latex]f(x)[/latex] be a function defined at all values in an open interval containing [latex]a[/latex], with the possible exception of [latex]a[/latex] itself, and let [latex]L[/latex] be a real number. Then,
Infinite Limits
Evaluating the limit of a function at a point or evaluating the limit of a function from the right and left at a point helps us to characterize the behavior of a function around a given value. As we shall see, we can also describe the behavior of functions that do not have finite limits.
We now turn our attention to [latex]h(x)=1/(x-2)^2,[/latex] (see (Figure 2.47) right hand side image). From its graph we see that as the values of [latex]x[/latex] approach 2, the values of [latex]h(x)=1/(x-2)^2[/latex] become larger and larger and, in fact, become infinite. Mathematically, we say that the limit of [latex]h(x)[/latex] as [latex]x[/latex] approaches 2 is positive infinity. Symbolically, we express this idea as
More generally, we define infinite limits as follows:
Definition
We define three types of infinite limits.
Infinite limits from the left: Let [latex]f(x)[/latex] be a function defined at all values in an open interval of the form [latex](b,a)[/latex].
- If the values of [latex]f(x)[/latex] increase without bound as the values of [latex]x[/latex] (where [latex]x < a[/latex]) approach the number [latex]a,[/latex] then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] from the left is positive infinity and we write $$\underset{x\to a^-}{\lim}f(x)=+\infty$$
- If the values of [latex]f(x)[/latex] decrease without bound as the values of [latex]x[/latex] (where [latex]x < a[/latex]) approach the number [latex]a,[/latex] then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] from the left is negative infinity and we write $$\underset{x\to a^-}{\lim}f(x)=−\infty$$
Infinite limits from the right: Let [latex]f(x)[/latex] be a function defined at all values in an open interval of the form [latex](a,c)[/latex].
- If the values of [latex]f(x)[/latex] increase without bound as the values of [latex]x[/latex] (where [latex]x > a[/latex]) approach the number [latex]a,[/latex] then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] from the left is positive infinity and we write
$$\underset{x\to a^+}{\lim}f(x)=+\infty.$$ - If the values of [latex]f(x)[/latex] decrease without bound as the values of [latex]x[/latex] (where [latex]x > a[/latex]) approach the number [latex]a,[/latex] then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] from the left is negative infinity and we write
$$\underset{x\to a^+}{\lim}f(x)=−\infty$$
Two-sided infinite limit: Let [latex]f(x)[/latex] be defined for all [latex]x\ne a[/latex] in an open interval containing [latex]a[/latex].
- If the values of [latex]f(x)[/latex] increase without bound as the values of [latex]x[/latex] (where [latex]x\ne a[/latex]) approach the number [latex]a,[/latex] then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] is positive infinity and we write
$$\underset{x\to a}{\lim}f(x)=+\infty$$ - If the values of [latex]f(x)[/latex] decrease without bound as the values of [latex]x[/latex] (where [latex]x\ne a[/latex]) approach the number [latex]a,[/latex] then we say that the limit as [latex]x[/latex] approaches [latex]a[/latex] is negative infinity and we write
$$\underset{x\to a}{\lim}f(x)=−\infty$$
It is important to understand that when we write statements such as [latex]\underset{x\to a}{\lim}f(x)=+\infty[/latex] or [latex]\underset{x\to a}{\lim}f(x)=−\infty[/latex] we are describing the behavior of the function, as we have just defined it. We are not asserting that a limit exists. For the limit of a function [latex]f(x)[/latex] to exist at [latex]a[/latex], it must approach a real number [latex]L[/latex] as [latex]x[/latex] approaches [latex]a[/latex]. That said, if, for example, [latex]\underset{x\to a}{\lim}f(x)=+\infty[/latex], we always write [latex]\underset{x\to a}{\lim}f(x)=+\infty[/latex] rather than [latex]\underset{x\to a}{\lim}f(x)[/latex] DNE.
It is useful to point out that functions of the form [latex]f(x)=1/(x-a)^n[/latex], where [latex]n[/latex] is a positive integer, have infinite limits as [latex]x[/latex] approaches [latex]a[/latex] from either the left or right graphs below where these limits are summarized.
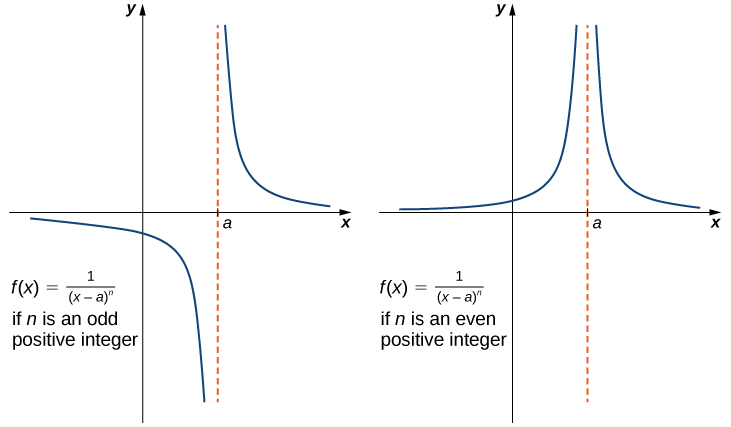
Long description: Two graphs side by side of f(x) = 1 / (x-a)^n. The first graph shows the case where n is an odd positive integer, and the second shows the case where n is an even positive integer. In the first, the graph has two segments. Each curve asymptotically towards the x axis, also known as y=0, and x=a. The segment to the left of x=a is below the x axis, and the segment to the right of x=a is above the x axis. In the second graph, both segments are above the x axis. In both graphs a vertical dashed line is shown at x = a.
Infinite Limits from Positive Integers
If [latex]n[/latex] is a positive even integer, then
$$\underset{x\to a}{\lim}\frac{1}{(x-a)^n}=+\infty$$
If [latex]n[/latex] is a positive odd integer, then
$$\underset{x\to a^+}{\lim}\frac{1}{(x-a)^n}=+\infty $$
and
$$\underset{x\to a^-}{\lim}\frac{1}{(x-a)^n}=−\infty$$
We should also point out that in the graphs of [latex]f(x)=1/(x-a)^n[/latex], points on the graph having [latex]x[/latex]-coordinates very near to [latex]a[/latex] are very close to the vertical line [latex]x=a[/latex]. That is, as [latex]x[/latex] approaches [latex]a[/latex], the points on the graph of [latex]f(x)[/latex] are closer to the line [latex]x=a[/latex]. The line [latex]x=a[/latex] is called a vertical asymptote of the graph. We formally define a vertical asymptote as follows:
Definition
Let [latex]f(x)[/latex] be a function. If any of the following conditions hold, then the line [latex]x=a[/latex] is a vertical asymptote of [latex]f(x)[/latex]:
In the next example we put our knowledge of various types of limits to use to analyze the behavior of a function at several different points.

