5.5 Differentiation of Log Functions
Derivative of the Logarithmic Function
Now that we have the derivative of the natural exponential function, we can use implicit differentiation to find the derivative of its inverse, the natural logarithmic function.
The Derivative of the Natural Logarithmic Function
If [latex]x>0[/latex] and [latex]y=\ln x[/latex], then
$$\frac{dy}{dx}=\frac{1}{x}$$
More generally, let [latex]g(x)[/latex] be a differentiable function. For all values of [latex]x[/latex] for which [latex]g^{\prime}(x)>0[/latex], the derivative of [latex]h(x)=\ln(g(x))[/latex] is given by
$$h^{\prime}(x)=\frac{1}{g(x)} g^{\prime}(x)$$
Proof
If [latex]x>0[/latex] and [latex]y=\ln x[/latex], then [latex]e^y=x.[/latex] Differentiating both sides of this equation results in the equation
$$e^y\frac{dy}{dx}=1.$$
Solving for [latex]\frac{dy}{dx}[/latex] yields
$$\frac{dy}{dx}=\frac{1}{e^y}.$$
Finally, we substitute [latex]x=e^y[/latex] to obtain
$$\frac{dy}{dx}=\frac{1}{x}.$$
We may also derive this result by applying the inverse function theorem, as follows. Since [latex]y=g(x)=\ln x[/latex] is the inverse of [latex]f(x)=e^x[/latex], by applying the inverse function theorem we have
$$\frac{dy}{dx}=\frac{1}{f^{\prime}(g(x))}=\frac{1}{e^{\ln x}}=\frac{1}{x}$$
Using this result and applying the chain rule to [latex]h(x)=\ln(g(x))[/latex] yields
$$h^{\prime}(x)=\frac{1}{g(x)} g^{\prime}(x).$$
The graph of [latex]y=\ln x[/latex] and its derivative [latex]\frac{dy}{dx}=\frac{1}{x}[/latex] are shown in the following figure.
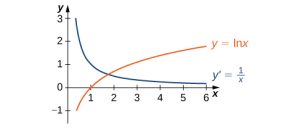
Long description: The function ln x is increasing on (0, + ∞). Its derivative is decreasing but greater than 0 on (0, + ∞).
Now that we can differentiate the natural logarithmic function, we can use this result to find the derivatives of [latex]y=\log_b x[/latex] and [latex]y=b^x[/latex] for [latex]b>0, \, b\ne 1[/latex].
Derivatives of General Exponential and Logarithmic Functions
Let [latex]b>0, \, b\ne 1[/latex], and let [latex]g(x)[/latex] be a differentiable function.
- If [latex]y=\log_b x[/latex], then
$$\frac{dy}{dx}=\frac{1}{x \ln b}.$$
More generally, if [latex]h(x)=\log_b (g(x))[/latex], then for all values of [latex]x[/latex] for which [latex]g(x)>0[/latex],
$$h^{\prime}(x)=\frac{g^{\prime}(x)}{g(x) \ln b}.$$ - If [latex]y=b^x[/latex], then
$$\frac{dy}{dx}=b^x \ln b.$$
More generally, if [latex]h(x)=b^{g(x)}[/latex], then
$$h^{\prime}(x)=b^{g(x)} g^{\prime}(x) \ln b$$
Proof
If [latex]y=\log_b x[/latex], then [latex]b^y=x[/latex]. It follows that [latex]\ln(b^y)=\ln x[/latex]. Thus [latex]y \ln b = \ln x[/latex]. Solving for [latex]y[/latex], we have [latex]y=\frac{\ln x}{\ln b}[/latex]. Differentiating and keeping in mind that [latex]\ln b[/latex] is a constant, we see that
$$\frac{dy}{dx}=\frac{1}{x \ln b}.$$
The derivative in (Figure) now follows from the chain rule.
If [latex]y=b^x[/latex], then [latex]\ln y=x \ln b[/latex]. Using implicit differentiation, again keeping in mind that [latex]\ln b[/latex] is constant, it follows that [latex]\frac{1}{y}\frac{dy}{dx}=\text{ln}b.[/latex] Solving for [latex]\frac{dy}{dx}[/latex] and substituting [latex]y=b^x[/latex], we see that
$$\frac{dy}{dx}=y \ln b=b^x \ln b.$$
The more general derivative, [latex]h^{\prime}(x)=b^{g(x)} g^{\prime}(x) \ln b,[/latex]
follows from the chain rule.
Logarithmic Differentiation
At this point, we can take derivatives of functions of the form [latex]y=(g(x))^n[/latex] for certain values of [latex]n[/latex], as well as functions of the form [latex]y=b^{g(x)}[/latex], where [latex]b>0[/latex] and [latex]b\ne 1[/latex]. Unfortunately, we still do not know the derivatives of functions such as [latex]y=x^x[/latex] or [latex]y=x^{\pi}[/latex]. These functions require a technique called logarithmic differentiation, which allows us to differentiate any function of the form [latex]h(x)=g(x)^{f(x)}[/latex]. It can also be used to convert a very complex differentiation problem into a simpler one, such as finding the derivative of [latex]y=\frac{x\sqrt{2x+1}}{e^x \sin^3 x}[/latex]. We outline this technique in the following problem-solving strategy.
Problem-Solving Strategy: Using Logarithmic Differentiation
- To differentiate [latex]y=h(x)[/latex] using logarithmic differentiation, take the natural logarithm of both sides of the equation to obtain [latex]\ln y=\ln (h(x))[/latex].
- Use properties of logarithms to expand [latex]\ln (h(x))[/latex] as much as possible.
- Differentiate both sides of the equation. On the left we will have [latex]\frac{1}{y}\frac{dy}{dx}[/latex].
- Multiply both sides of the equation by [latex]y[/latex] to solve for [latex]\frac{dy}{dx}[/latex].
- Replace [latex]y[/latex] by [latex]h(x)[/latex].

