"

Module 4: Discrete Random Variables

Poisson Distribution

Barbara Illowsky & OpenStax et al.

There are two main characteristics of a Poisson experiment.

  1. The Poisson probability distribution gives the probability of a number of events occurring in a fixed interval of time or space if these events happen with a known average rate and independently of the time since the last event. For example, a book editor might be interested in the number of words spelled incorrectly in a particular book. It might be that, on the average, there are five words spelled incorrectly in 100 pages. The interval is the 100 pages.
  2. The Poisson distribution may be used to approximate the binomial if the probability of success is “small” (such as 0.01) and the number of trials is “large” (such as 1,000). You will verify the relationship in the homework exercises. n is the number of trials, and p is the probability of a “success.”

The random variable X= the number of occurrences in the interval of interest.

Example

The average number of loaves of bread put on a shelf in a bakery in a half-hour period is 12. Of interest is the number of loaves of bread put on the shelf in five minutes. The time interval of interest is five minutes. What is the probability that the number of loaves, selected randomly, put on the shelf in five minutes is three?

[reveal-answer q=”869903″]Show Solution[/reveal-answer]
[hidden-answer a=”869903″]

Let X= the number of loaves of bread put on the shelf in five minutes. If the average number of loaves put on the shelf in 30 minutes (half-hour) is 12, then the average number of loaves put on the shelf in five minutes is left(frac530right)left(12right)=2 loaves of bread.

The probability question asks you to find P(x=3).

[/hidden-answer]

Notation for the Poisson: P= Poisson Probability Distribution Function

XsimP(mu)

Read this as “X is a random variable with a Poisson distribution.” The parameter is mu (or lambda); mu (or lambda)= the mean for the interval of interest.

Example

Leah’s answering machine receives about six telephone calls between 8 a.m. and 10 a.m. What is the probability that Leah receives more than one call in the next 15 minutes?

[reveal-answer q=”877222″]Show Solution[/reveal-answer]
[hidden-answer a=”877222″]

Let X= the number of calls Leah receives in 15 minutes. (The interval of interest is 15 minutes or frac14 hour.)

x=0,1,2,3,...

If Leah receives, on the average, six telephone calls in two hours, and there are eight 15-minute intervals in two hours, then Leah receives left(frac18right)left(6right)=0.75 calls in 15 minutes, on average. So, mu=0.75 for this problem.

XsimP(0.75)

Find P(x>1). P(x>1)=0.1734 (calculator or computer)

  • Press 1 – and then press 2nd DISTR.
  • Arrow down to poissoncdf. Press ENTER.
  • Enter (.75,1).
  • The result is P(x>1)=0.1734.

Note: The TI calculators use lambda (lambda) for the mean.

The probability that Leah receives more than one telephone call in the next 15 minutes is about 0.1734:

P(x>1)=1−textpoissoncdf(0.75,1)

The graph of XsimP(0.75) is:

This graphs shows a poisson probability distribution. It has 5 bars that decrease in height from left to right. The x-axis shows values in increments of 1 starting with 0, representing the number of calls Leah receives within 15 minutes. The y-axis ranges from 0 to 0.5 in increments of 0.1.

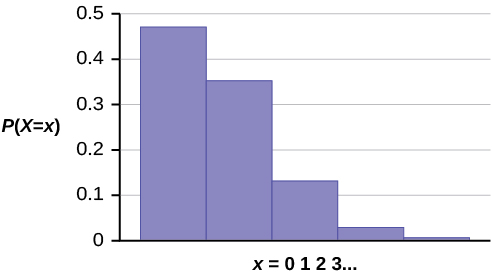
The y-axis contains the probability of x where X= the number of calls in 15 minutes.

[/hidden-answer]

Example

According to Baydin, an email management company, an email user gets, on average, 147 emails per day. Let X= the number of emails an email user receives per day. The discrete random variable X takes on the values x=0, 1, 2 …. The random variable X has a Poisson distribution: XsimP(147). The mean is 147 emails.

  1. What is the probability that an email user receives exactly 160 emails per day?
  2. What is the probability that an email user receives at most 160 emails per day?
  3. What is the standard deviation?

[reveal-answer q=”372382″]Show Solution[/reveal-answer]
[hidden-answer a=”372382″]

  1. P(x=160)=textpoissonpdf(147,160)approx0.0180
  2. P(xleq160)=textpoissoncdf(147,160)approx0.8666
  3. Standard Deviation=sigma=sqrtmu=sqrt144approx12.1244

[/hidden-answer]

Review

A Poisson probability distribution of a discrete random variable gives the probability of a number of events occurring in a fixed interval of time or space, if these events happen at a known average rate and independently of the time since the last event. The Poisson distribution may be used to approximate the binomial, if the probability of success is “small” (less than or equal to 0.05) and the number of trials is “large” (greater than or equal to 20).

Formula Review

XsimP(mu) means that X has a Poisson probability distribution where X= the number of occurrences in the interval of interest.

X takes on the values x=0, 1, 2, 3, …

The mean μ is typically given.

The variance is σ2=mu, and the standard deviation is  sigma=sqrtmu.

When P(μ) is used to approximate a binomial distribution, mu=np where n represents the number of independent trials and p represents the probability of success in a single trial.

License

Icon for the Creative Commons Attribution 4.0 International License

Poisson Distribution Copyright © 2018 by Barbara Illowsky & OpenStax et al. is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book