Module 12: Linear Regression and Correlation

Section Exercises

Barbara Illowsky & OpenStax et al.

Linear Equations

Use the following information to answer the next three exercises. A vacation resort rents SCUBA equipment to certified divers. The resort charges an up-front fee of $25 and another fee of $12.50 an hour.

1. What are the dependent and independent variables?
2. Find the equation that expresses the total fee in terms of the number of hours the equipment is rented.
3. Graph the equation from 2.
 Use the following information to answer the next two exercises. A credit card company charges $10 when a payment is late, and $5 a day each day the payment remains unpaid.

4. Find the equation that expresses the total fee in terms of the number of days the payment is late.

5. Graph the equation from 4.

6. Is the equation y = 10 + 5x – 3x2 linear? Why or why not?

7. Which of the following equations are linear?

a. y = 6x + 8

b. y + 7 = 3x

c. y – x = 8x2

d. 4y = 8

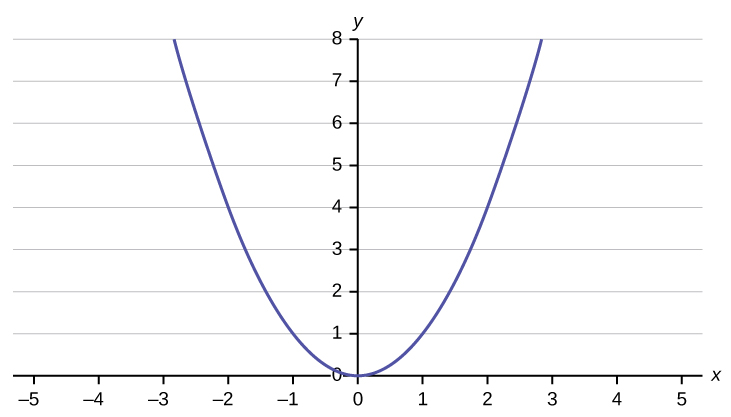
8. Does the graph show a linear equation? Why or why not?

This is a graph of an equation. The x-axis is labeled in intervals of 1 from -5 to 5; the y-axis is labeled in intervals of 1 from 0 - 8. The equation's graph is a parabola, a u-shaped curve that has a minimum value at (0, 0).

The table below contains real data for the first two decades of AIDS reporting.

Adults and Adolescents only, United States
Year # AIDS cases diagnosed # AIDS deaths
Pre-1981 91 29
1981 319 121
1982 1,170 453
1983 3,076 1,482
1984 6,240 3,466
1985 11,776 6,878
1986 19,032 11,987
1987 28,564 16,162
1988 35,447 20,868
1989 42,674 27,591
1990 48,634 31,335
1991 59,660 36,560
1992 78,530 41,055
1993 78,834 44,730
1994 71,874 49,095
1995 68,505 49,456
1996 59,347 38,510
1997 47,149 20,736
1998 38,393 19,005
1999 25,174 18,454
2000 25,522 17,347
2001 25,643 17,402
2002 26,464 16,371
Total 802,118 489,093
9. Use the columns “year” and “# AIDS cases diagnosed. Why is “year” the independent variable and “# AIDS cases diagnosed.” the dependent variable (instead of the reverse)?

Use the following information to answer the next two exercises. A specialty cleaning company charges an equipment fee and an hourly labor fee. A linear equation that expresses the total amount of the fee the company charges for each session is y = 50 + 100x.

10. What are the independent and dependent variables?

11. What is the y-intercept and what is the slope? Interpret them using complete sentences.

Use the following information to answer the next three questions. Due to erosion, a river shoreline is losing several thousand pounds of soil each year. A linear equation that expresses the total amount of soil lost per year is y = 12,000x.

12. What are the independent and dependent variables?

13. How many pounds of soil does the shoreline lose in a year?

14. What is the y-intercept? Interpret its meaning.

Use the following information to answer the next two exercises. The price of a single issue of stock can fluctuate throughout the day. A linear equation that represents the price of stock for Shipment Express is y = 15 – 1.5x where x is the number of hours passed in an eight-hour day of trading.

15. What are the slope and y-intercept? Interpret their meaning.
16. If you owned this stock, would you want a positive or negative slope? Why?
17. For each of the following situations, state the independent variable and the dependent variable.

  • A study is done to determine if elderly drivers are involved in more motor vehicle fatalities than other drivers. The number of fatalities per 100,000 drivers is compared to the age of drivers.
  • A study is done to determine if the weekly grocery bill changes based on the number of family members.
  • Insurance companies base life insurance premiums partially on the age of the applicant.
  • Utility bills vary according to power consumption.
  • A study is done to determine if a higher education reduces the crime rate in a population.

18. Piece-rate systems are widely debated incentive payment plans. In a recent study of loan officer effectiveness, the following piece-rate system was examined:

% of goal reached < 80 80 100 120
Incentive n/a $4,000 with an additional $125 added per percentage point from 81–99% $6,500 with an additional $125 added per percentage point from 101–119% $9,500 with an additional $125 added per percentage point starting at 121%

19. If a loan officer makes 95% of his or her goal, write the linear function that applies based on the incentive plan table. In context, explain the y-intercept and slope.

Scatter Plots

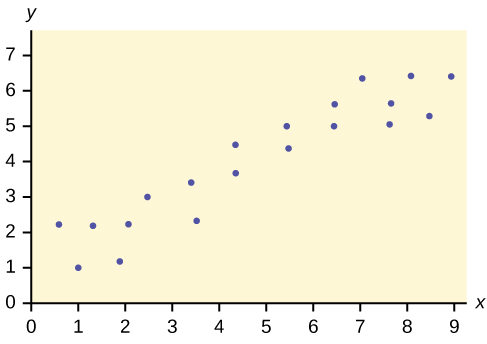
20. Does the scatter plot appear linear? Strong or weak? Positive or negative?

This is a scatterplot with several points plotted in the first quadrant. The points form a clear pattern, moving upward to the right. The points do not line up , but the overall pattern can be modeled with a line.
21. Does the scatter plot appear linear? Strong or weak? Positive or negative?

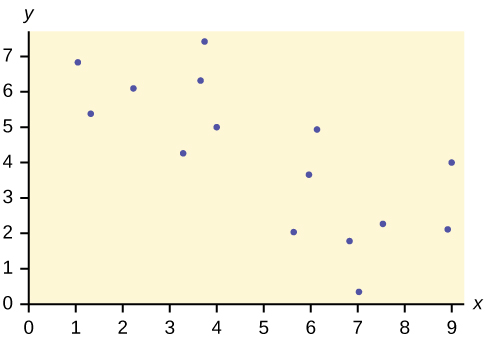
This is a scatterplot with several points plotted in the first quadrant. The points move downward to the right. The overall pattern can be modeled with a line, but the points are widely scattered.
22. Does the scatter plot appear linear? Strong or weak? Positive or negative?

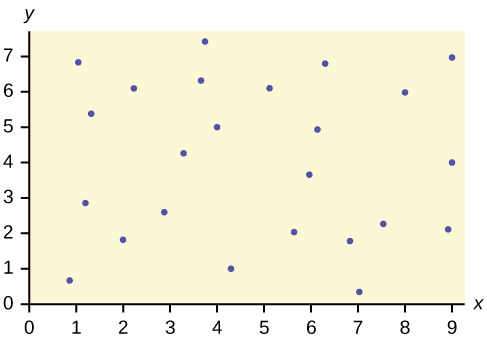
This is a scatter plot with several points plotted all over the first quadrant. There is no pattern.

23. The Gross Domestic Product Purchasing Power Parity is an indication of a country’s currency value compared to another country. The table below shows the GDP PPP of Cuba as compared to US dollars. Construct a scatter plot of the data.

 
Year Cuba’s PPP Year Cuba’s PPP
1999 1,700 2006 4,000
2000 1,700 2007 11,000
2002 2,300 2008 9,500
2003 2,900 2009 9,700
2004 3,000 2010 9,900
2005 3,500

24. The following table shows the poverty rates and cell phone usage in the United States. Construct a scatter plot of the data

Year Poverty Rate Cellular Usage per Capita
2003 12.7 54.67
2005 12.6 74.19
2007 12 84.86
2009 12 90.82

25. Does the higher cost of tuition translate into higher-paying jobs? The table lists the top ten colleges based on mid-career salary and the associated yearly tuition costs. Construct a scatter plot of the data.

 
School Mid-Career Salary (in thousands) Yearly Tuition
Princeton 137 28,540
Harvey Mudd 135 40,133
CalTech 127 39,900
US Naval Academy 122 0
West Point 120 0
MIT 118 42,050
Lehigh University 118 43,220
NYU-Poly 117 39,565
Babson College 117 40,400
Stanford 114 54,506
26. If the level of significance is 0.05 and the p-value is 0.06, what conclusion can you draw?

27. If there are 15 data points in a set of data, what is the number of degree of freedom?

The Regression Equation

Use the following information to answer the next five exercises. A random sample of ten professional athletes produced the following data where x is the number of endorsements the player has and y is the amount of money made (in millions of dollars).

 
x y x y
0 2 5 12
3 8 4 9
2 7 3 9
1 3 0 3
5 13 4 10
28. Draw a scatter plot of the data.
29. Use regression to find the equation for the line of best fit.
30. Draw the line of best fit on the scatter plot.
31. What is the slope of the line of best fit? What does it represent?
32. What is the y-intercept of the line of best fit? What does it represent?
33. What does an r value of zero mean?
34. When n = 2 and r = 1, are the data significant? Explain.

35. When n = 100 and r = -0.89, is there a significant correlation? Explain.

36. What is the process through which we can calculate a line that goes through a scatter plot with a linear pattern?

37. Explain what it means when a correlation has an r2 of 0.72.
38. Can a coefficient of determination be negative? Why or why not?

Testing the Significance of the Correlation Coefficient

39. When testing the significance of the correlation coefficient, what is the null hypothesis?

40. When testing the significance of the correlation coefficient, what is the alternative hypothesis?

41. If the level of significance is 0.05 and the p-value is 0.04, what conclusion can you draw?

42. If the level of significance is 0.05 and the p-value is 0.06, what conclusion can you draw?

43. If there are 15 data points in a set of data, what is the number of degree of freedom?

Prediction

Use the following information to answer the next two exercises. An electronics retailer used regression to find a simple model to predict sales growth in the first quarter of the new year (January through March). The model is good for 90 days, where x is the day. The model can be written as follows:

ŷ = 101.32 + 2.48x where ŷ is in thousands of dollars.

44. What would you predict the sales to be on day 60?
45. What would you predict the sales to be on day 90?

Use the following information to answer the next three exercises. A landscaping company is hired to mow the grass for several large properties. The total area of the properties combined is 1,345 acres. The rate at which one person can mow is as follows:ŷ = 1350 – 1.2x where x is the number of hours and ŷ represents the number of acres left to mow.

46. How many acres will be left to mow after 20 hours of work?

47. How many acres will be left to mow after 100 hours of work?

48. How many hours will it take to mow all of the lawns? (When is ŷ = 0?)

Table contains real data for the first two decades of AIDS reporting.

Adults and Adolescents only, United States
Year # AIDS cases diagnosed # AIDS deaths
Pre-1981 91 29
1981 319 121
1982 1,170 453
1983 3,076 1,482
1984 6,240 3,466
1985 11,776 6,878
1986 19,032 11,987
1987 28,564 16,162
1988 35,447 20,868
1989 42,674 27,591
1990 48,634 31,335
1991 59,660 36,560
1992 78,530 41,055
1993 78,834 44,730
1994 71,874 49,095
1995 68,505 49,456
1996 59,347 38,510
1997 47,149 20,736
1998 38,393 19,005
1999 25,174 18,454
2000 25,522 17,347
2001 25,643 17,402
2002 26,464 16,371
Total 802,118 489,093

49. Graph “year” versus “# AIDS cases diagnosed” (plot the scatter plot). Do not include pre-1981 data.

50. Perform linear regression. What is the linear equation? Round to the nearest whole number.

51. Write the equations:
Linear equation: __________
a = ________
b = ________
r = ________
n = ________

52. Solve.

When x = 1985, ŷ = _____
When x = 1990, ŷ =_____
When x = 1970, ŷ =______ Why doesn’t this answer make sense?

53. Does the line seem to fit the data? Why or why not?

54. What does the correlation imply about the relationship between time (years) and the number of diagnosed AIDS cases reported in the U.S.?

55. Plot the two given points on the following graph. Then, connect the two points to form the regression line.
Blank graph with horizontal and vertical axes.

Obtain the graph on your calculator or computer.

56. Write the equation: ŷ= ____________

57. Hand draw a smooth curve on the graph that shows the flow of the data.

58. Does the line seem to fit the data? Why or why not?

59. Do you think a linear fit is best? Why or why not?
60. What does the correlation imply about the relationship between time (years) and the number of diagnosed AIDS cases reported in the U.S.?
61. Graph “year” vs. “# AIDS cases diagnosed.” Do not include pre-1981. Label both axes with words. Scale both axes.
62. Enter your data into your calculator or computer. The pre-1981 data should not be included. Why is that so?

63. Write the linear equation, rounding to four decimal places:

64. Calculate the following:
  1. a = _____
  2. b = _____
  3. correlation = _____
  4. n = _____
65. Recently, the annual number of driver deaths per 100,000 for the selected age groups was as follows:

Age Number of Driver Deaths per 100,000
17.5 38
22 36
29.5 24
44.5 20
64.5 18
80 28
  1. For each age group, pick the midpoint of the interval for the x value. (For the 75+ group, use 80.)
  2. Using “ages” as the independent variable and “Number of driver deaths per 100,000” as the dependent variable, make a scatter plot of the data.
  3. Calculate the least squares (best–fit) line. Put the equation in the form of: ŷ = a + bx
  4. Find the correlation coefficient. Is it significant?
  5. Predict the number of deaths for ages 40 and 60.
  6. Based on the given data, is there a linear relationship between age of a driver and driver fatality rate?
  7. What is the slope of the least squares (best-fit) line? Interpret the slope.
66. The table below shows the life expectancy for an individual born in the United States in certain years.

Year of Birth Life Expectancy
1930 59.7
1940 62.9
1950 70.2
1965 69.7
1973 71.4
1982 74.5
1987 75
1992 75.7
2010 78.7
  1. Decide which variable should be the independent variable and which should be the dependent variable.
  2. Draw a scatter plot of the ordered pairs.
  3. Calculate the least squares line. Put the equation in the form of: ŷ = a + bx
  4. Find the correlation coefficient. Is it significant?
  5. Find the estimated life expectancy for an individual born in 1950 and for one born in 1982.
  6. Why aren’t the answers to part e the same as the values in Table that correspond to those years?
  7. Use the two points in part e to plot the least squares line on your graph from part b.
  8. Based on the data, is there a linear relationship between the year of birth and life expectancy?
  9. Are there any outliers in the data?
  10. Using the least squares line, find the estimated life expectancy for an individual born in 1850. Does the least squares line give an accurate estimate for that year? Explain why or why not.
  11. What is the slope of the least-squares (best-fit) line? Interpret the slope.

67. The maximum discount value of the Entertainment® card for the “Fine Dining” section, Edition ten, for various pages is given in the table below.

Page number Maximum value ($)
4 16
14 19
25 15
32 17
43 19
57 15
72 16
85 15
90 17
  1. Decide which variable should be the independent variable and which should be the dependent variable.
  2. Draw a scatter plot of the ordered pairs.
  3. Calculate the least-squares line. Put the equation in the form of: ŷ = a + bx
  4. Find the correlation coefficient. Is it significant?
  5. Find the estimated maximum values for the restaurants on page ten and on page 70.
  6. Does it appear that the restaurants giving the maximum value are placed in the beginning of the “Fine Dining” section? How did you arrive at your answer?
  7. Suppose that there were 200 pages of restaurants. What do you estimate to be the maximum value for a restaurant listed on page 200?
  8. Is the least squares line valid for page 200? Why or why not?
  9. What is the slope of the least-squares (best-fit) line? Interpret the slope.

68. The table below gives the gold medal times for every other Summer Olympics for the women’s 100-meter freestyle (swimming).

Year Time (seconds)
1912 82.2
1924 72.4
1932 66.8
1952 66.8
1960 61.2
1968 60.0
1976 55.65
1984 55.92
1992 54.64
2000 53.8
2008 53.1
  1. Decide which variable should be the independent variable and which should be the dependent variable.
  2. Draw a scatter plot of the data.
  3. Does it appear from inspection that there is a relationship between the variables? Why or why not?
  4. Calculate the least squares line. Put the equation in the form of: ŷ = a + bx.
  5. Find the correlation coefficient. Is the decrease in times significant?
  6. Find the estimated gold medal time for 1932. Find the estimated time for 1984.
  7. Why are the answers from part f different from the chart values?
  8. Does it appear that a line is the best way to fit the data? Why or why not?
  9. Use the least-squares line to estimate the gold medal time for the next Summer Olympics. Do you think that your answer is reasonable? Why or why not?
State # letters in name Year entered the Union Rank for entering the Union Area (square miles)
Alabama 7 1819 22 52,423
Colorado 8 1876 38 104,100
Hawaii 6 1959 50 10,932
Iowa 4 1846 29 56,276
Maryland 8 1788 7 12,407
Missouri 8 1821 24 69,709
New Jersey 9 1787 3 8,722
Ohio 4 1803 17 44,828
South Carolina 13 1788 8 32,008
Utah 4 1896 45 84,904
Wisconsin 9 1848 30 65,499

69. We are interested in whether or not the number of letters in a state name depends upon the year the state entered the Union.

  1. Decide which variable should be the independent variable and which should be the dependent variable.
  2. Draw a scatter plot of the data.
  3. Does it appear from inspection that there is a relationship between the variables? Why or why not?
  4. Calculate the least-squares line. Put the equation in the form of: ŷ = a + bx.
  5. Find the correlation coefficient. What does it imply about the significance of the relationship?
  6. Find the estimated number of letters (to the nearest integer) a state would have if it entered the Union in 1900. Find the estimated number of letters a state would have if it entered the Union in 1940.
  7. Does it appear that a line is the best way to fit the data? Why or why not?
  8. Use the least-squares line to estimate the number of letters a new state that enters the Union this year would have. Can the least squares line be used to predict it? Why or why not?

 

Outliers

Use the following information to answer the next four exercises. The scatter plot shows the relationship between hours spent studying and exam scores. The line shown is the calculated line of best fit. The correlation coefficient is 0.69.

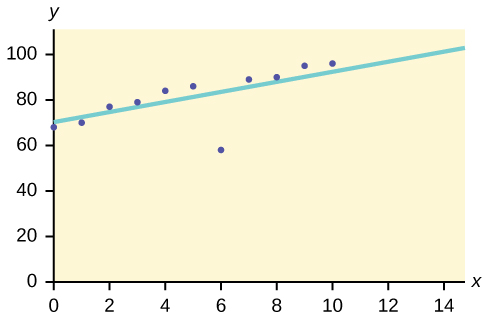
70. Do there appear to be any outliers?

71. A point is removed, and the line of best fit is recalculated. The new correlation coefficient is 0.98. Does the point appear to have been an outlier? Why?

72. What effect did the potential outlier have on the line of best fit?

73. Are you more or less confident in the predictive ability of the new line of best fit?

74. The Sum of Squared Errors for a data set of 18 numbers is 49. What is the standard deviation?

75. The Standard Deviation for the Sum of Squared Errors for a data set is 9.8. What is the cutoff for the vertical distance that a point can be from the line of best fit to be considered an outlier?
76. The height (sidewalk to roof) of notable tall buildings in America is compared to the number of stories of the building (beginning at street level).

Height (in feet) Stories
1,050 57
428 28
362 26
529 40
790 60
401 22
380 38
1,454 110
1,127 100
700 46
  1. Using “stories” as the independent variable and “height” as the dependent variable, make a scatter plot of the data.
  2. Does it appear from inspection that there is a relationship between the variables?
  3. Calculate the least squares line. Put the equation in the form of: ŷ = a + bx
  4. Find the correlation coefficient. Is it significant?
  5. Find the estimated heights for 32 stories and for 94 stories.
  6. Based on the data in Table, is there a linear relationship between the number of stories in tall buildings and the height of the buildings?
  7. Are there any outliers in the data? If so, which point(s)?
  8. What is the estimated height of a building with six stories? Does the least squares line give an accurate estimate of height? Explain why or why not.
  9. Based on the least squares line, adding an extra story is predicted to add about how many feet to a building?
  10. What is the slope of the least squares (best-fit) line? Interpret the slope.

77. Ornithologists, scientists who study birds, tag sparrow hawks in 13 different colonies to study their population. They gather data for the percent of new sparrow hawks in each colony and the percent of those that have returned from migration.

Percent return:74; 66; 81; 52; 73; 62; 52; 45; 62; 46; 60; 46; 38

Percent new:5; 6; 8; 11; 12; 15; 16; 17; 18; 18; 19; 20; 20

  1. Enter the data into your calculator and make a scatter plot.
  2. Use your calculator’s regression function to find the equation of the least-squares regression line. Add this to your scatter plot from part a.
  3. Explain in words what the slope and y-intercept of the regression line tell us.
  4. How well does the regression line fit the data? Explain your response.
  5. Which point has the largest residual? Explain what the residual means in context. Is this point an outlier? An influential point? Explain.
  6. An ecologist wants to predict how many birds will join another colony of sparrow hawks to which 70% of the adults from the previous year have returned. What is the prediction?

78. The following table shows data on average per capita wine consumption and heart disease rate in a random sample of 10 countries.

 
Yearly wine consumption in liters 2.5 3.9 2.9 2.4 2.9 0.8 9.1 2.7 0.8 0.7
Death from heart diseases 221 167 131 191 220 297 71 172 211 300
  1. Enter the data into your calculator and make a scatter plot.
  2. Use your calculator’s regression function to find the equation of the least-squares regression line. Add this to your scatter plot from part a.
  3. Explain in words what the slope and y-intercept of the regression line tell us.
  4. How well does the regression line fit the data? Explain your response.
  5. Which point has the largest residual? Explain what the residual means in context. Is this point an outlier? An influential point? Explain.
  6. Do the data provide convincing evidence that there is a linear relationship between the amount of alcohol consumed and the heart disease death rate? Carry out an appropriate test at a significance level of 0.05 to help answer this question.

79. The following table consists of one student athlete’s time (in minutes) to swim 2000 yards and the student’s heart rate (beats per minute) after swimming on a random sample of 10 days:

 
Swim Time Heart Rate
34.12 144
35.72 152
34.72 124
34.05 140
34.13 152
35.73 146
36.17 128
35.57 136
35.37 144
35.57 148
  1. Enter the data into your calculator and make a scatter plot.
  2. Use your calculator’s regression function to find the equation of the least-squares regression line. Add this to your scatter plot from part a.
  3. Explain in words what the slope and y-intercept of the regression line tell us.
  4. How well does the regression line fit the data? Explain your response.
  5. Which point has the largest residual? Explain what the residual means in context. Is this point an outlier? An influential point? Explain.

80. A researcher is investigating whether non-white minorities commit a disproportionate number of homicides. He uses demographic data from Detroit, MI to compare homicide rates and the number of the population that are white males.

 
White Males Homicide rate per 100,000 people
558,724 8.6
538,584 8.9
519,171 8.52
500,457 8.89
482,418 13.07
465,029 14.57
448,267 21.36
432,109 28.03
416,533 31.49
401,518 37.39
387,046 46.26
373,095 47.24
359,647 52.33
  1. Use your calculator to construct a scatter plot of the data. What should the independent variable be? Why?
  2. Use your calculator’s regression function to find the equation of the least-squares regression line. Add this to your scatter plot.
  3. Discuss what the following mean in context.
    1. The slope of the regression equation
    2. The y-intercept of the regression equation
    3. The correlation r
    4. The coefficient of determination r2.
  4. Do the data provide convincing evidence that there is a linear relationship between the number of white males in the population and the homicide rate? Carry out an appropriate test at a significance level of 0.05 to help answer this question.
 
School Mid-Career Salary (in thousands) Yearly Tuition
Princeton 137 28,540
Harvey Mudd 135 40,133
CalTech 127 39,900
US Naval Academy 122 0
West Point 120 0
MIT 118 42,050
Lehigh University 118 43,220
NYU-Poly 117 39,565
Babson College 117 40,400
Stanford 114 54,506

81. Using the data to determine the linear-regression line equation with the outliers removed. Is there a linear correlation for the data set with outliers removed? Justify your answer.

82. The average number of people in a family that received welfare for various years is given in Table.

Year Welfare family size
1969 4.0
1973 3.6
1975 3.2
1979 3.0
1983 3.0
1988 3.0
1991 2.9
  1. Using “year” as the independent variable and “welfare family size” as the dependent variable, draw a scatter plot of the data.
  2. Calculate the least-squares line. Put the equation in the form of: ŷ = a + bx
  3. Find the correlation coefficient. Is it significant?
  4. Pick two years between 1969 and 1991 and find the estimated welfare family sizes.
  5. Based on the data in Table, is there a linear relationship between the year and the average number of people in a welfare family?
  6. Using the least-squares line, estimate the welfare family sizes for 1960 and 1995. Does the least-squares line give an accurate estimate for those years? Explain why or why not.
  7. Are there any outliers in the data?
  8. What is the estimated average welfare family size for 1986? Does the least squares line give an accurate estimate for that year? Explain why or why not.
  9. What is the slope of the least squares (best-fit) line? Interpret the slope.
83. The percent of female wage and salary workers who are paid hourly rates is given in Table for the years 1979 to 1992.

Year Percent of workers paid hourly rates
1979 61.2
1980 60.7
1981 61.3
1982 61.3
1983 61.8
1984 61.7
1985 61.8
1986 62.0
1987 62.7
1990 62.8
1992 62.9
  1. Using “year” as the independent variable and “percent” as the dependent variable, draw a scatter plot of the data.
  2. Does it appear from inspection that there is a relationship between the variables? Why or why not?
  3. Calculate the least-squares line. Put the equation in the form of: ŷ = a + bx
  4. Find the correlation coefficient. Is it significant?
  5. Find the estimated percents for 1991 and 1988.
  6. Based on the data, is there a linear relationship between the year and the percent of female wage and salary earners who are paid hourly rates?
  7. Are there any outliers in the data?
  8. What is the estimated percent for the year 2050? Does the least-squares line give an accurate estimate for that year? Explain why or why not.
  9. What is the slope of the least-squares (best-fit) line? Interpret the slope.

Use the following information to answer the next two exercises. The cost of a leading liquid laundry detergent in different sizes is given in Table.

Size (ounces) Cost ($) Cost per ounce
16 3.99
32 4.99
64 5.99
200 10.99
84.

  1. Using “size” as the independent variable and “cost” as the dependent variable, draw a scatter plot.
  2. Does it appear from inspection that there is a relationship between the variables? Why or why not?
  3. Calculate the least-squares line. Put the equation in the form of: ŷ = a + bx
  4. Find the correlation coefficient. Is it significant?
  5. If the laundry detergent were sold in a 40-ounce size, find the estimated cost.
  6. If the laundry detergent were sold in a 90-ounce size, find the estimated cost.
  7. Does it appear that a line is the best way to fit the data? Why or why not?
  8. Are there any outliers in the given data?
  9. Is the least-squares line valid for predicting what a 300-ounce size of the laundry detergent would you cost? Why or why not?
  10. What is the slope of the least-squares (best-fit) line? Interpret the slope.

85.

  1. Complete Table for the cost per ounce of the different sizes.
  2. Using “size” as the independent variable and “cost per ounce” as the dependent variable, draw a scatter plot of the data.
  3. Does it appear from inspection that there is a relationship between the variables? Why or why not?
  4. Calculate the least-squares line. Put the equation in the form of: ŷ = a + bx
  5. Find the correlation coefficient. Is it significant?
  6. If the laundry detergent were sold in a 40-ounce size, find the estimated cost per ounce.
  7. If the laundry detergent were sold in a 90-ounce size, find the estimated cost per ounce.
  8. Does it appear that a line is the best way to fit the data? Why or why not?
  9. Are there any outliers in the the data?
  10. Is the least-squares line valid for predicting what a 300-ounce size of the laundry detergent would cost per ounce? Why or why not?
  11. What is the slope of the least-squares (best-fit) line? Interpret the slope.
86. According to a flyer by a Prudential Insurance Company representative, the costs of approximate probate fees and taxes for selected net taxable estates are as follows:

Net Taxable Estate ($) Approximate Probate Fees and Taxes ($)
600,000 30,000
750,000 92,500
1,000,000 203,000
1,500,000 438,000
2,000,000 688,000
2,500,000 1,037,000
3,000,000 1,350,000
  1. Decide which variable should be the independent variable and which should be the dependent variable.
  2. Draw a scatter plot of the data.
  3. Does it appear from inspection that there is a relationship between the variables? Why or why not?
  4. Calculate the least-squares line. Put the equation in the form of: ŷ = a + bx.
  5. Find the correlation coefficient. Is it significant?
  6. Find the estimated total cost for a next taxable estate of $1,000,000. Find the cost for $2,500,000.
  7. Does it appear that a line is the best way to fit the data? Why or why not?
  8. Are there any outliers in the data?
  9. Based on these results, what would be the probate fees and taxes for an estate that does not have any assets?
  10. What is the slope of the least-squares (best-fit) line? Interpret the slope.
87. The following are advertised sale prices of color televisions at Anderson’s.

Size (inches) Sale Price ($)
9 147
20 197
27 297
31 447
35 1177
40 2177
60 2497
  1. Decide which variable should be the independent variable and which should be the dependent variable.
  2. Draw a scatter plot of the data.
  3. Does it appear from inspection that there is a relationship between the variables? Why or why not?
  4. Calculate the least-squares line. Put the equation in the form of: ŷ = a + bx
  5. Find the correlation coefficient. Is it significant?
  6. Find the estimated sale price for a 32 inch television. Find the cost for a 50 inch television.
  7. Does it appear that a line is the best way to fit the data? Why or why not?
  8. Are there any outliers in the data?
  9. What is the slope of the least-squares (best-fit) line? Interpret the slope.

88. Table shows the average heights for American boy s in 1990.

Age (years) Height (cm)
birth 50.8
2 83.8
3 91.4
5 106.6
7 119.3
10 137.1
14 157.5
  1. Decide which variable should be the independent variable and which should be the dependent variable.
  2. Draw a scatter plot of the data.
  3. Does it appear from inspection that there is a relationship between the variables? Why or why not?
  4. Calculate the least-squares line. Put the equation in the form of: ŷ = a + bx
  5. Find the correlation coefficient. Is it significant?
  6. Find the estimated average height for a one-year-old. Find the estimated average height for an eleven-year-old.
  7. Does it appear that a line is the best way to fit the data? Why or why not?
  8. Are there any outliers in the data?
  9. Use the least squares line to estimate the average height for a sixty-two-year-old man. Do you think that your answer is reasonable? Why or why not?
  10. What is the slope of the least-squares (best-fit) line? Interpret the slope.
 
State # letters in name Year entered the Union Ranks for entering the Union Area (square miles)
Alabama 7 1819 22 52,423
Colorado 8 1876 38 104,100
Hawaii 6 1959 50 10,932
Iowa 4 1846 29 56,276
Maryland 8 1788 7 12,407
Missouri 8 1821 24 69,709
New Jersey 9 1787 3 8,722
Ohio 4 1803 17 44,828
South Carolina 13 1788 8 32,008
Utah 4 1896 45 84,904
Wisconsin 9 1848 30 65,499

89. We are interested in whether there is a relationship between the ranking of a state and the area of the state.

  1. What are the independent and dependent variables?
  2. What do you think the scatter plot will look like? Make a scatter plot of the data.
  3. Does it appear from inspection that there is a relationship between the variables? Why or why not?
  4. Calculate the least-squares line. Put the equation in the form of: ŷ = a + bx
  5. Find the correlation coefficient. What does it imply about the significance of the relationship?
  6. Find the estimated areas for Alabama and for Colorado. Are they close to the actual areas?
  7. Use the two points in part f to plot the least-squares line on your graph from part b.
  8. Does it appear that a line is the best way to fit the data? Why or why not?
  9. Are there any outliers?
  10. Use the least squares line to estimate the area of a new state that enters the Union. Can the least-squares line be used to predict it? Why or why not?
  11. Delete “Hawaii” and substitute “Alaska” for it. Alaska is the forty-ninth, state with an area of 656,424 square miles.
  12. Calculate the new least-squares line.
  13. Find the estimated area for Alabama. Is it closer to the actual area with this new least-squares line or with the previous one that included Hawaii? Why do you think that’s the case?
  14. Do you think that, in general, newer states are larger than the original states?

 

License

Icon for the Creative Commons Attribution 4.0 International License

Section Exercises Copyright © 2018 by Barbara Illowsky & OpenStax et al. is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book