Module 13: F-Distribution and One-Way ANOVA

Section Exercises

Barbara Illowsky & OpenStax et al.

One-Way ANOVA

Use the following information to answer the next five exercises. There are five basic assumptions that must be fulfilled in order to perform a one-way ANOVA test. What are they?

1. Write one assumption.
2. Write another assumption.
3. Write a third assumption.
4. Write a fourth assumption.
5. Write the final assumption.
6. State the null hypothesis for a one-way ANOVA test if there are four groups.
7. State the alternative hypothesis for a one-way ANOVA test if there are three groups.
8. When do you use an ANOVA test?
9. Three different traffic routes are tested for mean driving time. The entries in the table are the driving times in minutes on the three different routes. The one-way ANOVA results are shown in Table.

Route 1 Route 2 Route 3
30 27 16
32 29 41
27 28 22
35 36 31

10. State SSbetween, SSwithin, and the F statistic.

11. Suppose a group is interested in determining whether teenagers obtain their drivers licenses at approximately the same average age across the country. Suppose that the following data are randomly collected from five teenagers in each region of the country. The numbers represent the age at which teenagers obtained their drivers licenses.
Northeast South West Central East
16.3 16.9 16.4 16.2 17.1
16.1 16.5 16.5 16.6 17.2
16.4 16.4 16.6 16.5 16.6
16.5 16.2 16.1 16.4 16.8
[latex]overline{x}[/latex]= ________ ________ ________ ________ ________
[latex]{s}_{2}[/latex]= ________ ________ ________ ________ ________

12. State the hypotheses.

H0: ____________

Ha: ____________

The F Distribution and the F-Ratio

Use the following information to answer the next eight exercises. Groups of men from three different areas of the country are to be tested for mean weight. The entries in the table are the weights for the different groups. The one-way ANOVA results are shown in Table.

Group 1 Group 2 Group 3
216 202 170
198 213 165
240 284 182
187 228 197
176 210 201
13. What is the Sum of Squares Factor?
14. What is the Sum of Squares Error?
15. What is the df for the numerator?
16. What is the df for the denominator?

17. What is the Mean Square Factor?

18. What is the Mean Square Error?
19. What is the F statistic?
Use the following information to answer the next eight exercises. Girls from four different soccer teams are to be tested for mean goals scored per game. The entries in the table are the goals per game for the different teams. The one-way ANOVA results are shown in Table.
Team 1 Team 2 Team 3 Team 4
1 2 0 3
2 3 1 4
0 2 1 4
3 4 0 3
2 4 0 2
20. What is SSbetween?
21. What is the df for the numerator?
22. What is MSbetween?
23. What is SSwithin?
24. What is the df for the denominator?
25. What is MSwithin?
26. What is the F statistic?
27. Judging by the F statistic, do you think it is likely or unlikely that you will reject the null hypothesis?
Use the following information to answer the next three exercises. Suppose a group is interested in determining whether teenagers obtain their drivers licenses at approximately the same average age across the country. Suppose that the following data are randomly collected from five teenagers in each region of the country. The numbers represent the age at which teenagers obtained their drivers licenses.

Northeast South West Central East
16.3 16.9 16.4 16.2 17.1
16.1 16.5 16.5 16.6 17.2
16.4 16.4 16.6 16.5 16.6
16.5 16.2 16.1 16.4 16.8
[latex]overline{x}[/latex]= ________ ________ ________ ________ ________
[latex]{s}_{2}[/latex] ________ ________ ________ ________ ________

28. H0: µ1 = µ2 = µ3 = µ4 = µ5

29. Hα: At least any two of the group means µ1, µ2, …, µ5 are not equal.

30. degrees of freedom – numerator: df(num) = _________

31. degrees of freedom – denominator: df(denom) = ________
32. F statistic = ________

Facts About the F Distribution

33. An F statistic can have what values?
34. What happens to the curves as the degrees of freedom for the numerator and the denominator get larger?
Use the following information to answer the next seven exercise. Four basketball teams took a random sample of players regarding how high each player can jump (in inches). The results are shown in Table.
Team 1 Team 2 Team 3 Team 4 Team 5
36 32 48 38 41
42 35 50 44 39
51 38 39 46 40
35. What is the df(num)?
36. What is the df(denom)?
37. What are the Sum of Squares and Mean Squares Factors?
38. What are the Sum of Squares and Mean Squares Errors?
39. What is the F statistic?
40. What is the p-value?
41. At the 5% significance level, is there a difference in the mean jump heights among the teams?
Use the following information to answer the next seven exercises. A video game developer is testing a new game on three different groups. Each group represents a different target market for the game. The developer collects scores from a random sample from each group. The results are shown in Table
Group A Group B Group C
101 151 101
108 149 109
98 160 198
107 112 186
111 126 160
42. What is the df(num)?
43. What is the df(denom)?
44. What are the SSbetween and MSbetween?
45. What are the SSwithin and MSwithin?
46. What is the F Statistic?
47. What is the p-value?

48. At the 10% significance level, are the scores among the different groups different?

 Use the following information to answer the next three exercises. Suppose a group is interested in determining whether teenagers obtain their drivers licenses at approximately the same average age across the country. Suppose that the following data are randomly collected from five teenagers in each region of the country. The numbers represent the age at which teenagers obtained their drivers licenses.
Northeast South West Central East
16.3 16.9 16.4 16.2 17.1
16.1 16.5 16.5 16.6 17.2
16.4 16.4 16.6 16.5 16.6
16.5 16.2 16.1 16.4 16.8
[latex]overline{x}[/latex]= ________ ________ ________ ________ ________
[latex]{s}_{2}[/latex]= ________ ________ ________ ________ ________

49. Enter the data into your calculator or computer.

50. p-value = ______

 State the decisions and conclusions (in complete sentences) for the following preconceived levels of α.

51. α = 0.05

a. Decision: ____________________________

b. Conclusion: ____________________________

52. α = 0.01

a. Decision: ____________________________

b. Conclusion: ____________________________

DIRECTIONS

Use a solution sheet to conduct the following hypothesis tests. The solution sheet can be found in Appendix E.

53. Three students, Linda, Tuan, and Javier, are given five laboratory rats each for a nutritional experiment. Each rat’s weight is recorded in grams. Linda feeds her rats Formula A, Tuan feeds his rats Formula B, and Javier feeds his rats Formula C. At the end of a specified time period, each rat is weighed again, and the net gain in grams is recorded. Using a significance level of 10%, test the hypothesis that the three formulas produce the same mean weight gain.

Weights of Student Lab Rats
Linda’s rats Tuan’s rats Javier’s rats
43.5 47.0 51.2
39.4 40.5 40.9
41.3 38.9 37.9
46.0 46.3 45.0
38.2 44.2 48.6
54. A grassroots group opposed to a proposed increase in the gas tax claimed that the increase would hurt working-class people the most, since they commute the farthest to work. Suppose that the group randomly surveyed 24 individuals and asked them their daily one-way commuting mileage. The results are in Table.  Using a 5% significance level, test the hypothesis that the three mean commuting mileages are the same.

working-class professional (middle incomes) professional (wealthy)
17.8 16.5 8.5
26.7 17.4 6.3
49.4 22.0 4.6
9.4 7.4 12.6
65.4 9.4 11.0
47.1 2.1 28.6
19.5 6.4 15.4
51.2 13.9 9.3
55. Examine the seven practice laps from Appendix C. Determine whether the mean lap time is statistically the same for the seven practice laps, or if there is at least one lap that has a different mean time from the others.
Use the following information to answer the next two exercises. Table lists the number of pages in four different types of magazines.
home decorating news health computer
172 87 82 104
286 94 153 136
163 123 87 98
205 106 103 207
197 101 96 146
56. Using a significance level of 5%, test the hypothesis that the four magazine types have the same mean length.
57. Eliminate one magazine type that you now feel has a mean length different from the others. Redo the hypothesis test, testing that the remaining three means are statistically the same. Use a new solution sheet. Based on this test, are the mean lengths for the remaining three magazines statistically the same?
58. A researcher wants to know if the mean times (in minutes) that people watch their favorite news station are the same. Suppose that Table shows the results of a study.
CNN FOX Local
45 15 72
12 43 37
18 68 56
38 50 60
23 31 51
35 22

59. Assume that all distributions are normal, the four population standard deviations are approximately the same, and the data were collected independently and randomly. Use a level of significance of 0.05.

60. Are the means for the final exams the same for all statistics class delivery types? Table shows the scores on final exams from several randomly selected classes that used the different delivery types.

Online Hybrid Face-to-Face
72 83 80
84 73 78
77 84 84
80 81 81
81 86
79
82

61. Assume that all distributions are normal, the four population standard deviations are approximately the same, and the data were collected independently and randomly. Use a level of significance of 0.05.

62. Are the mean number of times a month a person eats out the same for whites, blacks, Hispanics and Asians? Suppose that Table shows the results of a study.
White Black Hispanic Asian
6 4 7 8
8 1 3 3
2 5 5 5
4 2 4 1
6 6 7

63. Assume that all distributions are normal, the four population standard deviations are approximately the same, and the data were collected independently and randomly. Use a level of significance of 0.05.

64. Are the mean numbers of daily visitors to a ski resort the same for the three types of snow conditions? Suppose that Table shows the results of a study.

Powder Machine Made Hard Packed
1,210 2,107 2,846
1,080 1,149 1,638
1,537 862 2,019
941 1,870 1,178
1,528 2,233
1,382

65. Assume that all distributions are normal, the four population standard deviations are approximately the same, and the data were collected independently and randomly. Use a level of significance of 0.05.

66. Sanjay made identical paper airplanes out of three different weights of paper, light, medium and heavy. He made four airplanes from each of the weights, and launched them himself across the room. Here are the distances (in meters) that his planes flew.
Paper Type/Trial Trial 1 Trial 2 Trial 3 Trial 4
Heavy 5.1 meters 3.1 meters 4.7 meters 5.3 meters
Medium 4 meters 3.5 meters 4.5 meters 6.1 meters
Light 3.1 meters 3.3 meters 2.1 meters 1.9 meters
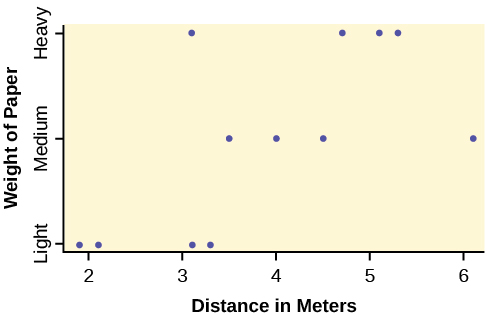
the graph is a scatter plot which represents the data provided. The horizontal axis is labeled 'Distance in Meters,' and extends form 2 to 6. The vertical axis is labeled 'Weight of Paper' and has light, medium, and heavy categories.
  1. Take a look at the data in the graph. Look at the spread of data for each group (light, medium, heavy). Does it seem reasonable to assume a normal distribution with the same variance for each group? Yes or No.
  2. Why is this a balanced design?
  3. Calculate the sample mean and sample standard deviation for each group.
  4. Does the weight of the paper have an effect on how far the plane will travel? Use a 1% level of significance. Complete the test using the method shown in the bean plant example in Example.
    • variance of the group means __________
    • MSbetween= ___________
    • mean of the three sample variances ___________
    • MSwithin = _____________
    • F statistic = ____________
    • df(num) = __________, df(denom) = ___________
    • number of groups _______
    • number of observations _______
    • p-value = __________ (P(F > _______) = __________)
    • Graph the p-value.
    • decision: _______________________
    • conclusion: _______________________________________________________________
67. DDT is a pesticide that has been banned from use in the United States and most other areas of the world. It is quite effective, but persisted in the environment and over time became seen as harmful to higher-level organisms. Famously, egg shells of eagles and other raptors were believed to be thinner and prone to breakage in the nest because of ingestion of DDT in the food chain of the birds.

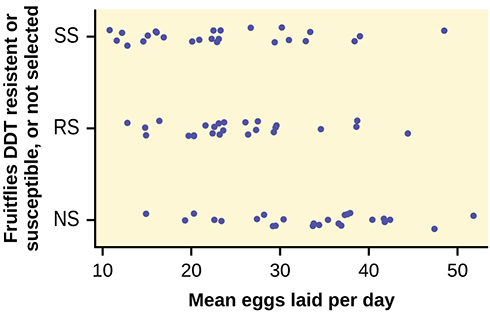
68. An experiment was conducted on the number of eggs (fecundity) laid by female fruit flies. There are three groups of flies. One group was bred to be resistant to DDT (the RS group). Another was bred to be especially susceptible to DDT (SS). Finally there was a control line of non-selected or typical fruitflies (NS). Here are the data:

RS SS NS RS SS NS
12.8 38.4 35.4 22.4 23.1 22.6
21.6 32.9 27.4 27.5 29.4 40.4
14.8 48.5 19.3 20.3 16 34.4
23.1 20.9 41.8 38.7 20.1 30.4
34.6 11.6 20.3 26.4 23.3 14.9
19.7 22.3 37.6 23.7 22.9 51.8
22.6 30.2 36.9 26.1 22.5 33.8
29.6 33.4 37.3 29.5 15.1 37.9
16.4 26.7 28.2 38.6 31 29.5
20.3 39 23.4 44.4 16.9 42.4
29.3 12.8 33.7 23.2 16.1 36.6
14.9 14.6 29.2 23.6 10.8 47.4
27.3 12.2 41.7

69. The values are the average number of eggs laid daily for each of 75 flies (25 in each group) over the first 14 days of their lives. Using a 1% level of significance, are the mean rates of egg selection for the three strains of fruitfly different? If so, in what way? Specifically, the researchers were interested in whether or not the selectively bred strains were different from the nonselected line, and whether the two selected lines were different from each other.

Here is a chart of the three groups:

This graph is a scatterplot which represents the data provided. The horizontal axis is labeled 'Mean eggs laid per day' and extends from 10 - 50. The vertical axis is labeled 'Fruitflies DDT resistant or susceptible, or not selected.' The vertical axis is labeled with the categories NS, RS, SS.

70. The data shown is the recorded body temperatures of 130 subjects as estimated from available histograms.

71. Traditionally we are taught that the normal human body temperature is 98.6 F. This is not quite correct for everyone. Are the mean temperatures among the four groups different?

72. Calculate 95% confidence intervals for the mean body temperature in each group and comment about the confidence intervals.

99.198.699.5  99.198.6   99.298.7   99.499.1   99.999.3   10099.4   100.8

FL FH ML MH FL FH ML MH
96.4 96.8 96.3 96.9 98.4 98.6 98.1 98.6
96.7 97.7 96.7 97 98.7 98.6 98.1 98.6
97.2 97.8 97.1 97.1 98.7 98.6 98.2 98.7
97.2 97.9 97.2 97.1 98.7 98.7 98.2 98.8
97.4 98 97.3 97.4 98.7 98.7 98.2 98.8
97.6 98 97.4 97.5 98.8 98.8 98.2 98.8
97.7 98 97.4 97.6 98.8 98.8 98.3 98.9
97.8 98 97.4 97.7 98.8 98.8 98.4 99
97.8 98.1 97.5 97.8 98.8 98.9 98.4 99
97.9 98.3 97.6 97.9 99.2 99 98.5 99
97.9 98.3 97.6 98 99.3 99 98.5 99.2
98 98.3 97.8 98
98.2 98.4 97.8 98
98.2 98.4 97.8 98.3
98.2 98.4 97.9 98.4
98.2 98.4 98 98.4
98.2 98.5 98 98.6
98.2 98.6 98 98.6

Test of Two Variances

Use the following information to answer the next two exercises. There are two assumptions that must be true in order to perform an F test of two variances.

73. Name one assumption that must be true.
74. What is the other assumption that must be true?

Use the following information to answer the next five exercises. Two coworkers commute from the same building. They are interested in whether or not there is any variation in the time it takes them to drive to work. They each record their times for 20 commutes. The first worker’s times have a variance of 12.1. The second worker’s times have a variance of 16.9. The first worker thinks that he is more consistent with his commute times and that his commute time is shorter. Test the claim at the 10% level.

75. State the null and alternative hypotheses.
76. What is s1 in this problem?
77. What is s2 in this problem?
78. What is n?
79. What is the F statistic?
80. What is the p-value?
81. Is the claim accurate?
Use the following information to answer the next four exercises. Two students are interested in whether or not there is variation in their test scores for math class. There are 15 total math tests they have taken so far. The first student’s grades have a standard deviation of 38.1. The second student’s grades have a standard deviation of 22.5. The second student thinks his scores are lower.
82. State the null and alternative hypotheses.
83. What is the F Statistic?
84. What is the p-value?
85. At the 5% significance level, do we reject the null hypothesis?
Use the following information to answer the next three exercises. Two cyclists are comparing the variances of their overall paces going uphill. Each cyclist records his or her speeds going up 35 hills. The first cyclist has a variance of 23.8 and the second cyclist has a variance of 32.1. The cyclists want to see if their variances are the same or different.
86. State the null and alternative hypotheses.
87. What is the F Statistic?
88. At the 5% significance level, what can we say about the cyclists’ variances?

89. Three students, Linda, Tuan, and Javier, are given five laboratory rats each for a nutritional experiment. Each rat’s weight is recorded in grams. Linda feeds her rats Formula A, Tuan feeds his rats Formula B, and Javier feeds his rats Formula C. At the end of a specified time period, each rat is weighed again and the net gain in grams is recorded.

Linda’s rats Tuan’s rats Javier’s rats
43.5 47.0 51.2
39.4 40.5 40.9
41.3 38.9 37.9
46.0 46.3 45.0
38.2 44.2 48.6

90. Determine whether or not the variance in weight gain is statistically the same among Javier’s and Linda’s rats. Test at a significance level of 10%.

91. A grassroots group opposed to a proposed increase in the gas tax claimed that the increase would hurt working-class people the most, since they commute the farthest to work. Suppose that the group randomly surveyed 24 individuals and asked them their daily one-way commuting mileage. The results are as follows.
working-class professional (middle incomes) professional (wealthy)
17.8 16.5 8.5
26.7 17.4 6.3
49.4 22.0 4.6
9.4 7.4 12.6
65.4 9.4 11.0
47.1 2.1 28.6
19.5 6.4 15.4
51.2 13.9 9.3

92. Determine whether or not the variance in mileage driven is statistically the same among the working class and professional (middle income) groups. Use a 5% significance level.

Refer to the data from Appendix C.

93. Examine practice laps 3 and 4. Determine whether or not the variance in lap time is statistically the same for those practice laps.

Use the following information to answer the next two exercises. The following table lists the number of pages in four different types of magazines.

home decorating news health computer
172 87 82 104
286 94 153 136
163 123 87 98
205 106 103 207
197 101 96 146
94. Which two magazine types do you think have the same variance in length?

95. Which two magazine types do you think have different variances in length?

96. Is the variance for the amount of money, in dollars, that shoppers spend on Saturdays at the mall the same as the variance for the amount of money that shoppers spend on Sundays at the mall? Suppose that the Table shows the results of a study.
Saturday Sunday Saturday Sunday
75 44 62 137
18 58 0 82
150 61 124 39
94 19 50 127
62 99 31 141
73 60 118 73
89

97. Are the variances for incomes on the East Coast and the West Coast the same? Suppose that Table shows the results of a study. Income is shown in thousands of dollars. Assume that both distributions are normal. Use a level of significance of 0.05.

East West
38 71
47 126
30 42
82 51
75 44
52 90
115 88
67

98. Thirty men in college were taught a method of finger tapping. They were randomly assigned to three groups of ten, with each receiving one of three doses of caffeine: 0 mg, 100 mg, 200 mg. This is approximately the amount in no, one, or two cups of coffee. Two hours after ingesting the caffeine, the men had the rate of finger tapping per minute recorded. The experiment was double blind, so neither the recorders nor the students knew which group they were in. Does caffeine affect the rate of tapping, and if so how?

Here are the data:

0 mg 100 mg 200 mg 0 mg 100 mg 200 mg
242 248 246 245 246 248
244 245 250 248 247 252
247 248 248 248 250 250
242 247 246 244 246 248
246 243 245 242 244 250
99. King Manuel I, Komnenus ruled the Byzantine Empire from Constantinople (Istanbul) during the years 1145 to 1180 A.D. The empire was very powerful during his reign, but declined significantly afterwards. Coins minted during his era were found in Cyprus, an island in the eastern Mediterranean Sea. Nine coins were from his first coinage, seven from the second, four from the third, and seven from a fourth. These spanned most of his reign. We have data on the silver content of the coins:

6.2  5.8  5.8

First Coinage Second Coinage Third Coinage Fourth Coinage
5.9 6.9 4.9 5.3
6.8 9.0 5.5 5.6
6.4 6.6 4.6 5.5
7.0 8.1 4.5 5.1
6.6 9.3
7.7 9.2
7.2 8.6
6.9
6.2

100. Did the silver content of the coins change over the course of Manuel’s reign?

101. Here are the means and variances of each coinage. The data are unbalanced.

First Second Third Fourth
Mean 6.7444 8.2429 4.875 5.6143
Variance 0.2953 1.2095 0.2025 0.1314
102. The American League and the National League of Major League Baseball are each divided into three divisions: East, Central, and West. Many years, fans talk about some divisions being stronger (having better teams) than other divisions. This may have consequences for the postseason. For instance, in 2012 Tampa Bay won 90 games and did not play in the postseason, while Detroit won only 88 and did play in the postseason. This may have been an oddity, but is there good evidence that in the 2012 season, the American League divisions were significantly different in overall records? Use the following data to test whether the mean number of wins per team in the three American League divisions were the same or not. Note that the data are not balanced, as two divisions had five teams, while one had only four.

Division Team Wins
East NY Yankees 95
East Baltimore 93
East Tampa Bay 90
East Toronto 73
East Boston 69
Division Team Wins
Central Detroit 88
Central Chicago Sox 85
Central Kansas City 72
Central Cleveland 68
Central Minnesota 66
Division Team Wins
West Oakland 94
West Texas 93
West LA Angels 89
West Seattle 75

License

Icon for the Creative Commons Attribution 4.0 International License

Section Exercises Copyright © 2018 by Barbara Illowsky & OpenStax et al. is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book