Module 2: Descriptive Statistics

Section Exercises

Barbara Illowsky & OpenStax et al.

Stem-and-Leaf Graphs (Stemplots), Line Graphs, and Bar Graphs

For each of the following data sets, create a stem plot and identify any outliers.

1. The miles per gallon rating for 30 cars are shown below (lowest to highest).  19, 19, 19, 20, 21, 21, 25, 25, 25, 26, 26, 28, 29, 31, 31, 32, 32, 33, 34, 35, 36, 37, 37, 38, 38, 38, 38, 41, 43, 43

2. The height in feet of 25 trees is shown below (lowest to highest).  25, 27, 33, 34, 34, 34, 35, 37, 37, 38, 39, 39, 39, 40, 41, 45, 46, 47, 49, 50, 50, 53, 53, 54, 54

3. The data are the prices of different laptops at an electronics store. Round each value to the nearest ten.  249, 249, 260, 265, 265, 280, 299, 299, 309, 319, 325, 326, 350, 350, 350, 365, 369, 389, 409, 459, 489, 559, 569, 570, 610

4. The data are daily high temperatures in a town for one month.  61, 61, 62, 64, 66, 67, 67, 67, 68, 69, 70, 70, 70, 71, 71, 72, 74, 74, 74, 75, 75, 75, 76, 76, 77, 78, 78, 79, 79, 95
For the next three exercises, use the data to construct a line graph.

In a survey, 40 people were asked how many times they visited a store before making a major purchase. The results are shown in the table.

Number of times in store Frequency
1 4
2 10
3 16
4 6
5 4
In a survey, several people were asked how many years it has been since they purchased a mattress. The results are shown in the table.
Years since last purchase Frequency
0 2
1 8
2 13
3 22
4 16
5 9

Several children were asked how many TV shows they watch each day. The results of the survey are shown in the table.

Number of TV Shows Frequency
0 12
1 18
2 36
3 7
4 2
The students in Ms. Ramirez’s math class have birthdays in each of the four seasons. The table shows the four seasons, the number of students who have birthdays in each season, and the percentage (%) of students in each group. Construct a bar graph showing the number of students.
Seasons Number of students Proportion of population
Spring 8 24%
Summer 9 26%
Autumn 11 32%
Winter 6 18%

5. Using the data from Mrs. Ramirez’s math class supplied in the tables, construct a bar graph showing the percentages.

6. David County has six high schools. Each school sent students to participate in a county-wide science competition. The table shows the percentage breakdown of competitors from each school, and the percentage of the entire student population of the county that goes to each school. Construct a bar graph that shows the population percentage of competitors from each school.
High School Science competition population Overall student population
Alabaster 28.9% 8.6%
Concordia 7.6% 23.2%
Genoa 12.1% 15.0%
Mocksville 18.5% 14.3%
Tynneson 24.2% 10.1%
West End 8.7% 28.8%

7. Use the data from the David County science competition supplied in the table above. Construct a bar graph that shows the county-wide population percentage of students at each school.

8. Student grades on a chemistry exam were: 77, 78, 76, 81, 86, 51, 79, 82, 84, 99

  1. Construct a stem-and-leaf plot of the data.
  2. Are there any potential outliers? If so, which scores are they? Why do you consider them outliers?

9. The table contains the 2010 obesity rates in U.S. states and Washington, DC.

State Percent (%) State Percent (%) State Percent (%)
Alabama 32.2 Kentucky 31.3 North Dakota 27.2
Alaska 24.5 Louisiana 31.0 Ohio 29.2
Arizona 24.3 Maine 26.8 Oklahoma 30.4
Arkansas 30.1 Maryland 27.1 Oregon 26.8
California 24.0 Massachusetts 23.0 Pennsylvania 28.6
Colorado 21.0 Michigan 30.9 Rhode Island 25.5
Connecticut 22.5 Minnesota 24.8 South Carolina 31.5
Delaware 28.0 Mississippi 34.0 South Dakota 27.3
Washington, DC 22.2 Missouri 30.5 Tennessee 30.8
Florida 26.6 Montana 23.0 Texas 31.0
Georgia 29.6 Nebraska 26.9 Utah 22.5
Hawaii 22.7 Nevada 22.4 Vermont 23.2
Idaho 26.5 New Hampshire 25.0 Virginia 26.0
Illinois 28.2 New Jersey 23.8 Washington 25.5
Indiana 29.6 New Mexico 25.1 West Virginia 32.5
Iowa 28.4 New York 23.9 Wisconsin 26.3
Kansas 29.4 North Carolina 27.8 Wyoming 25.1
  1. Use a random number generator to randomly pick eight states. Construct a bar graph of the obesity rates of those eight states.
  2. Construct a bar graph for all the states beginning with the letter “A.”
  3. Construct a bar graph for all the states beginning with the letter “M.”

Histograms, Frequency Polygons, and Time Series Graphs

10. Sixty-five randomly selected car salespersons were asked the number of cars they generally sell in one week. Fourteen people answered that they generally sell three cars; nineteen generally sell four cars; twelve generally sell five cars; nine generally sell six cars; eleven generally sell seven cars. Complete the table.

Data Value (# cars) Frequency Relative Frequency Cumulative Relative Frequency

11. What does the frequency column in Table sum to? Why?

12. What does the relative frequency column in Table sum to? Why?

13. What is the difference between relative frequency and frequency for each data value in Table?

14. What is the difference between cumulative relative frequency and relative frequency for each data value?

15. To construct the histogram for the data in Table, determine appropriate minimum and maximum x and y values and the scaling. Sketch the histogram. Label the horizontal and vertical axes with words. Include numerical scaling.

An empty graph template for use with this question.

16. Construct a frequency polygon for the following:

  1. Pulse Rates for Women Frequency
    60–69 12
    70–79 14
    80–89 11
    90–99 1
    100–109 1
    110–119 0
    120–129 1
  2. Actual Speed in a 30 MPH Zone Frequency
    42–45 25
    46–49 14
    50–53 7
    54–57 3
    58–61 1
  3. Tar (mg) in Nonfiltered Cigarettes Frequency
    10–13 1
    14–17 0
    18–21 15
    22–25 7
    26–29 2

17. Construct a frequency polygon from the frequency distribution for the 50 highest ranked countries for depth of hunger.

Depth of Hunger Frequency
230–259 21
260–289 13
290–319 5
320–349 7
350–379 1
380–409 1
410–439 1

18. Use the two frequency tables to compare the life expectancy of men and women from 20 randomly selected countries. Include an overlayed frequency polygon and discuss the shapes of the distributions, the center, the spread, and any outliers. What can we conclude about the life expectancy of women compared to men?

Life Expectancy at Birth – Women Frequency
49–55 3
56–62 3
63–69 1
70–76 3
77–83 8
84–90 2
Life Expectancy at Birth – Men Frequency
49–55 3
56–62 3
63–69 1
70–76 1
77–83 7
84–90 5

19. Construct a times series graph for (a) the number of male births, (b) the number of female births, and (c) the total number of births.

Sex/Year 1855 1856 1857 1858 1859 1860 1861
Female 45,545 49,582 50,257 50,324 51,915 51,220 52,403
Male 47,804 52,239 53,158 53,694 54,628 54,409 54,606
Total 93,349 101,821 103,415 104,018 106,543 105,629 107,009
Sex/Year 1862 1863 1864 1865 1866 1867 1868 1869
Female 51,812 53,115 54,959 54,850 55,307 55,527 56,292 55,033
Male 55,257 56,226 57,374 58,220 58,360 58,517 59,222 58,321
Total 107,069 109,341 112,333 113,070 113,667 114,044 115,514 113,354
Sex/Year 1871 1870 1872 1871 1872 1827 1874 1875
Female 56,099 56,431 57,472 56,099 57,472 58,233 60,109 60,146
Male 60,029 58,959 61,293 60,029 61,293 61,467 63,602 63,432
Total 116,128 115,390 118,765 116,128 118,765 119,700 123,711 123,578

20. The following data sets list full time police per 100,000 citizens along with homicides per 100,000 citizens for the city of Detroit, Michigan during the period from 1961 to 1973.

Year 1961 1962 1963 1964 1965 1966 1967
Police 260.35 269.8 272.04 272.96 272.51 261.34 268.89
Homicides 8.6 8.9 8.52 8.89 13.07 14.57 21.36
Year 1968 1969 1970 1971 1972 1973
Police 295.99 319.87 341.43 356.59 376.69 390.19
Homicides 28.03 31.49 37.39 46.26 47.24 52.33
  1. Construct a double time series graph using a common x-axis for both sets of data.
  2. Which variable increased the fastest? Explain.
  3. Did Detroit’s increase in police officers have an impact on the murder rate? Explain.

21. Suppose that three book publishers were interested in the number of fiction paperbacks adult consumers purchase per month. Each publisher conducted a survey. In the survey, adult consumers were asked the number of fiction paperbacks they had purchased the previous month. The results are as follows:

Publisher A
# of books Freq. Rel. Freq.
0 10
1 12
2 16
3 12
4 8
5 6
6 2
8 2
Publisher B
# of books Freq. Rel. Freq.
0 18
1 24
2 24
3 22
4 15
5 10
7 5
9 1
Publisher C
# of books Freq. Rel. Freq.
0–1 20
2–3 35
4–5 12
6–7 2
8–9 1
  1. Find the relative frequencies for each survey. Write them in the charts.
  2. Using either a graphing calculator, computer, or by hand, use the frequency column to construct a histogram for each publisher’s survey. For Publishers A and B, make bar widths of one. For Publisher C, make bar widths of two.
  3. In complete sentences, give two reasons why the graphs for Publishers A and B are not identical.
  4. Would you have expected the graph for Publisher C to look like the other two graphs? Why or why not?
  5. Make new histograms for Publisher A and Publisher B. This time, make bar widths of two.
  6. Now, compare the graph for Publisher C to the new graphs for Publishers A and B. Are the graphs more similar or more different? Explain your answer.

22. Often, cruise ships conduct all on-board transactions, with the exception of gambling, on a cashless basis. At the end of the cruise, guests pay one bill that covers all onboard transactions. Suppose that 60 single travelers and 70 couples were surveyed as to their on-board bills for a seven-day cruise from Los Angeles to the Mexican Riviera. Following is a summary of the bills for each group.

Singles
Amount($) Frequency Rel. Frequency
51–100 5
101–150 10
151–200 15
201–250 15
251–300 10
301–350 5
Couples
Amount($) Frequency Rel. Frequency
100–150 5
201–250 5
251–300 5
301–350 5
351–400 10
401–450 10
451–500 10
501–550 10
551–600 5
601–650 5
  1. Fill in the relative frequency for each group.
  2. Construct a histogram for the singles group. Scale the x-axis by $50 widths. Use relative frequency on the y-axis.
  3. Construct a histogram for the couples group. Scale the x-axis by $50 widths. Use relative frequency on the y-axis.
  4. Compare the two graphs:
    1. List two similarities between the graphs.
    2. List two differences between the graphs.
    3. Overall, are the graphs more similar or different?
  5. Construct a new graph for the couples by hand. Since each couple is paying for two individuals, instead of scaling the x-axis by $50, scale it by $100. Use relative frequency on the y-axis.
  6. Compare the graph for the singles with the new graph for the couples:
    1. List two similarities between the graphs.
    2. Overall, are the graphs more similar or different?
  7. How did scaling the couples graph differently change the way you compared it to the singles graph?
  8. Based on the graphs, do you think that individuals spend the same amount, more or less, as singles as they do person by person as a couple? Explain why in one or two complete sentences.

22. Twenty-five randomly selected students were asked the number of movies they watched the previous week. The results are as follows.

# of movies Frequency Relative Frequency Cumulative Relative Frequency
0 5
1 9
2 6
3 4
4 1
  1. Construct a histogram of the data.
  2. Complete the columns of the chart.

Use the following information to answer the next two exercises:

Suppose one hundred eleven people who shopped in a special t-shirt store were asked the number of t-shirts they own costing more than $19 each.

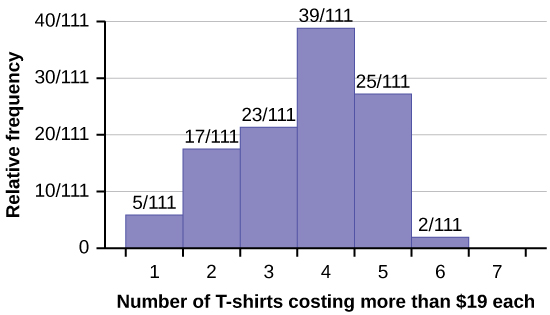
A histogram showing the results of a survey. Of 111 respondents, 5 own 1 t-shirt costing more than $19, 17 own 2, 23 own 3, 39 own 4, 25 own 5, 2 own 6, and no respondents own 7.

23. The percentage of people who own at most three t-shirts costing more than $19 each is approximately:

  1. 21
  2. 59
  3. 41
  4. Cannot be determined
24. If the data were collected by asking the first 111 people who entered the store, then the type of sampling is:

  1. cluster
  2. simple random
  3. stratified
  4. convenience

25. Following are the 2010 obesity rates by U.S. states and Washington, DC.

State Percent (%) State Percent (%) State Percent (%)
Alabama 32.2 Kentucky 31.3 North Dakota 27.2
Alaska 24.5 Louisiana 31.0 Ohio 29.2
Arizona 24.3 Maine 26.8 Oklahoma 30.4
Arkansas 30.1 Maryland 27.1 Oregon 26.8
California 24.0 Massachusetts 23.0 Pennsylvania 28.6
Colorado 21.0 Michigan 30.9 Rhode Island 25.5
Connecticut 22.5 Minnesota 24.8 South Carolina 31.5
Delaware 28.0 Mississippi 34.0 South Dakota 27.3
Washington, DC 22.2 Missouri 30.5 Tennessee 30.8
Florida 26.6 Montana 23.0 Texas 31.0
Georgia 29.6 Nebraska 26.9 Utah 22.5
Hawaii 22.7 Nevada 22.4 Vermont 23.2
Idaho 26.5 New Hampshire 25.0 Virginia 26.0
Illinois 28.2 New Jersey 23.8 Washington 25.5
Indiana 29.6 New Mexico 25.1 West Virginia 32.5
Iowa 28.4 New York 23.9 Wisconsin 26.3
Kansas 29.4 North Carolina 27.8 Wyoming 25.1

26. Construct a bar graph of obesity rates of your state and the four states closest to your state. Hint: Label the x-axis with the states.

Measures of the Location of the Data

27. Listed are 29 ages for Academy Award winning best actors in order from smallest to largest.

18; 21; 22; 25; 26; 27; 29; 30; 31; 33; 36; 37; 41; 42; 47; 52; 55; 57; 58; 62; 64; 67; 69; 71; 72; 73; 74; 76; 77

  1. Find the 40th percentile.
  2. Find the 78th percentile.

28. Listed are 32 ages for Academy Award winning best actors in order from smallest to largest.

18; 18; 21; 22; 25; 26; 27; 29; 30; 31; 31; 33; 36; 37; 37; 41; 42; 47; 52; 55; 57; 58; 62; 64; 67; 69; 71; 72; 73; 74; 76; 77

  1. Find the percentile of 37.
  2. Find the percentile of 72.

29. Jesse was ranked 37th in his graduating class of 180 students. At what percentile is Jesse’s ranking?

  1. For runners in a race, a low time means a faster run. The winners in a race have the shortest running times. Is it more desirable to have a finish time with a high or a low percentile when running a race?
  2. The 20th percentile of run times in a particular race is 5.2 minutes. Write a sentence interpreting the 20th percentile in the context of the situation.
  3. A bicyclist in the 90th percentile of a bicycle race completed the race in 1 hour and 12 minutes. Is he among the fastest or slowest cyclists in the race? Write a sentence interpreting the 90th percentile in the context of the situation.
  4. For runners in a race, a higher speed means a faster run. Is it more desirable to have a speed with a high or a low percentile when running a race?
  5. The 40th percentile of speeds in a particular race is 7.5 miles per hour. Write a sentence interpreting the 40th percentile in the context of the situation.

30. On an exam, would it be more desirable to earn a grade with a high or low percentile? Explain.

31. Mina is waiting in line at the Department of Motor Vehicles (DMV). Her wait time of 32 minutes is the 85th percentile of wait times. Is that good or bad? Write a sentence interpreting the 85th percentile in the context of this situation.

32. In a survey collecting data about the salaries earned by recent college graduates, Li found that her salary was in the 78th percentile. Should Li be pleased or upset by this result? Explain.

33. In a study collecting data about the repair costs of damage to automobiles in a certain type of crash tests, a certain model of car had $1,700 in damage and was in the 90th percentile. Should the manufacturer and the consumer be pleased or upset by this result? Explain and write a sentence that interprets the 90th percentile in the context of this problem.

34. The University of California has two criteria used to set admission standards for freshman to be admitted to a college in the UC system:
  1. Students’ GPAs and scores on standardized tests (SATs and ACTs) are entered into a formula that calculates an “admissions index” score. The admissions index score is used to set eligibility standards intended to meet the goal of admitting the top 12% of high school students in the state. In this context, what percentile does the top 12% represent?
  2. Students whose GPAs are at or above the 96th percentile of all students at their high school are eligible (called eligible in the local context), even if they are not in the top 12% of all students in the state. What percentage of students from each high school are “eligible in the local context”?

35. Suppose that you are buying a house. You and your realtor have determined that the most expensive house you can afford is the 34th percentile. The 34th percentile of housing prices is $240,000 in the town you want to move to. In this town, can you afford 34% of the houses or 66% of the houses?

36. Use 35 to calculate the following values:
First quartile = _______
Second quartile = median = 50th percentile = _______
Third quartile = _______
Interquartile range (IQR) = _____ – _____ = _____
10th percentile = _______

70th percentile = _______

37. The median age for U.S. blacks currently is 30.9 years; for U.S. whites it is 42.3 years.Based upon this information, give two reasons why the black median age could be lower than the white median age. Does the lower median age for blacks necessarily mean that blacks die younger than whites? Why or why not? How might it be possible for blacks and whites to die at approximately the same age, but for the median age for whites to be higher?

38. Six hundred adult Americans were asked by telephone poll, “What do you think constitutes a middle-class income?” The results are in the table. Also, include left endpoint, but not the right endpoint.

Salary ($) Relative Frequency
< 20,000 0.02
20,000–25,000 0.09
25,000–30,000 0.19
30,000–40,000 0.26
40,000–50,000 0.18
50,000–75,000 0.17
75,000–99,999 0.02
100,000+ 0.01
  1. What percentage of the survey answered “not sure”?
  2. What percentage think that middle-class is from $25,000 to $50,000?
  3. Construct a histogram of the data.
    1. Should all bars have the same width, based on the data? Why or why not?
    2. How should the <20,000 and the 100,000+ intervals be handled? Why?
  4. Find the 40th and 80th percentiles
  5. Construct a bar graph of the data

39. Given the following box plot:

This is a horizontal boxplot graphed over a number line from 0 to 13. The first whisker extends from the smallest value, 0, to the first quartile, 2. The box begins at the first quartile and extends to third quartile, 12. A vertical, dashed line is drawn at median, 10. The second whisker extends from the third quartile to largest value, 13.
  1. which quarter has the smallest spread of data? What is that spread?
  2. which quarter has the largest spread of data? What is that spread?
  3. find the interquartile range (IQR).
  4. are there more data in the interval 5–10 or in the interval 10–13? How do you know this?
  5. which interval has the fewest data in it? How do you know this?
    1. 0–2
    2. 2–4
    3. 10–12
    4. 12–13
    5. need more information

40. The following box plot shows the U.S. population for 1990, the latest available year.

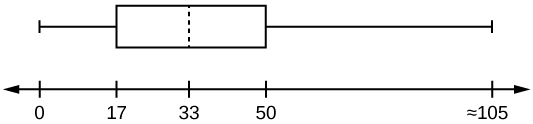
A box plot with values from 0 to 105, with Q1 at 17, M at 33, and Q3 at 50.
  1. Are there fewer or more children (age 17 and under) than senior citizens (age 65 and over)? How do you know?
  2. 12.6% are age 65 and over. Approximately what percentage of the population are working age adults (above age 17 to age 65)?

Box Plots

41. In a survey of 20-year-olds in China, Germany, and the United States, people were asked the number of foreign countries they had visited in their lifetime. The following box plots display the results.

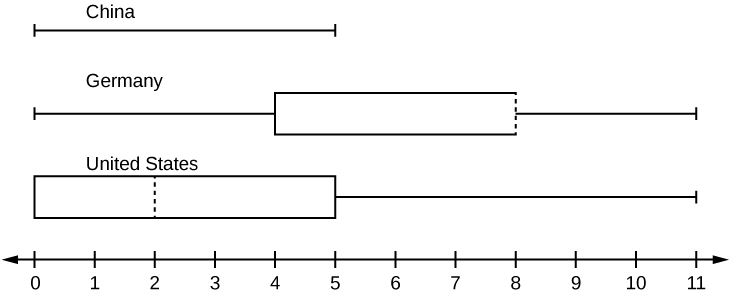
This shows three boxplots graphed over a number line from 0 to 11. The boxplots match the supplied data, and compare the countries' results. The China boxplot has a single whisker from 0 to 5. The Germany box plot's median is equal to the third quartile, so there is a dashed line at right edge of box. The America boxplot does not have a left whisker.
  1. In complete sentences, describe what the shape of each box plot implies about the distribution of the data collected.
  2. Have more Americans or more Germans surveyed been to over eight foreign countries?
  3. Compare the three box plots. What do they imply about the foreign travel of 20-year-old residents of the three countries when compared to each other?

42. Given the following box plot, answer the questions.

This is a boxplot graphed over a number line from 0 to 150. There is no first, or left, whisker. The box starts at the first quartile, 0, and ends at the third quartile, 80. A vertical, dashed line marks the median, 20. The second whisker extends the third quartile to the largest value, 150.
  1. Think of an example (in words) where the data might fit into the above box plot. In 2–5 sentences, write down the example.
  2. What does it mean to have the first and second quartiles so close together, while the second to third quartiles are far apart?

43. Given the following box plots, answer the questions.

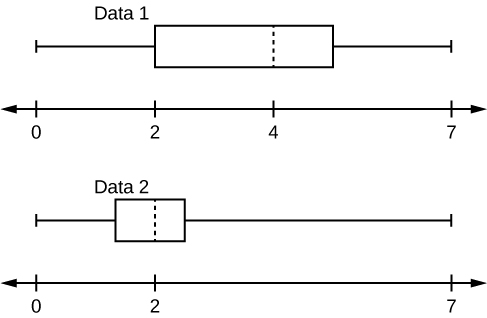
This shows two boxplots graphed over number lines from 0 to 7. The first whisker in the data 1 boxplot extends from 0 to 2. The box begins at the firs quartile, 2, and ends at the third quartile, 5. A vertical, dashed line marks the median at 4. The second whisker extends from the third quartile to the largest value, 7. The first whisker in the data 2 box plot extends from 0 to 1.3. The box begins at the first quartile, 1.3, and ends at the third quartile, 2.5. A vertical, dashed line marks the medial at 2. The second whisker extends from the third quartile to the largest value, 7.
  1. In complete sentences, explain why each statement is false.
    1. Data 1 has more data values above two than Data 2 has above two.
    2. The data sets cannot have the same mode.
    3. For Data 1, there are more data values below four than there are above four.
  2. For which group, Data 1 or Data 2, is the value of “7” more likely to be an outlier? Explain why in complete sentences.

44. A survey was conducted of 130 purchasers of new BMW 3 series cars, 130 purchasers of new BMW 5 series cars, and 130 purchasers of new BMW 7 series cars. In it, people were asked the age they were when they purchased their car. The following box plots display the results.

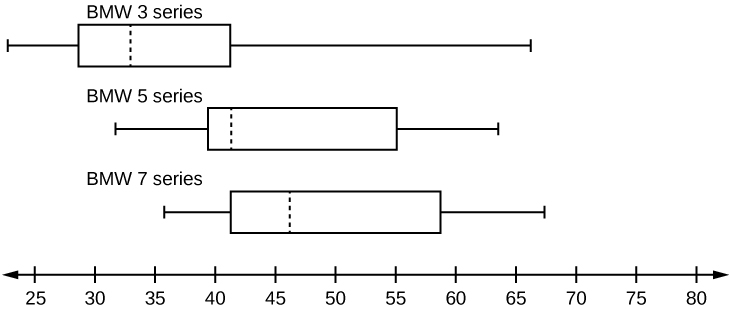
This shows three boxplots graphed over a number line from 25 to 80. The first whisker on the BMW 3 plot extends from 25 to 30. The box begins at the firs quartile, 30 and ends at the thir quartile, 41. A verical, dashed line marks the median at 34. The second whisker extends from the third quartile to 66. The first whisker on the BMW 5 plot extends from 31 to 40. The box begins at the firs quartile, 40, and ends at the third quartile, 55. A vertical, dashed line marks the median at 41. The second whisker extends from 55 to 64. The first whisker on the BMW 7 plot extends from 35 to 41. The box begins at the first quartile, 41, and ends at the third quartile, 59. A vertical, dashed line marks the median at 46. The second whisker extends from 59 to 68.
  1. In complete sentences, describe what the shape of each box plot implies about the distribution of the data collected for that car series.
  2. Which group is most likely to have an outlier? Explain how you determined that.
  3. Compare the three box plots. What do they imply about the age of purchasing a BMW from the series when compared to each other?
  4. Look at the BMW 5 series. Which quarter has the smallest spread of data? What is the spread?
  5. Look at the BMW 5 series. Which quarter has the largest spread of data? What is the spread?
  6. Look at the BMW 5 series. Estimate the interquartile range (IQR).
  7. Look at the BMW 5 series. Are there more data in the interval 31 to 38 or in the interval 45 to 55? How do you know this?
  8. Look at the BMW 5 series. Which interval has the fewest data in it? How do you know this?
    1. 31–35
    2. 38–41
    3. 41–64
 45. Twenty-five randomly selected students were asked the number of movies they watched the previous week. The results are as follows:
# of movies Frequency
0 5
1 9
2 6
3 4
4 1

Construct a box plot of the data.

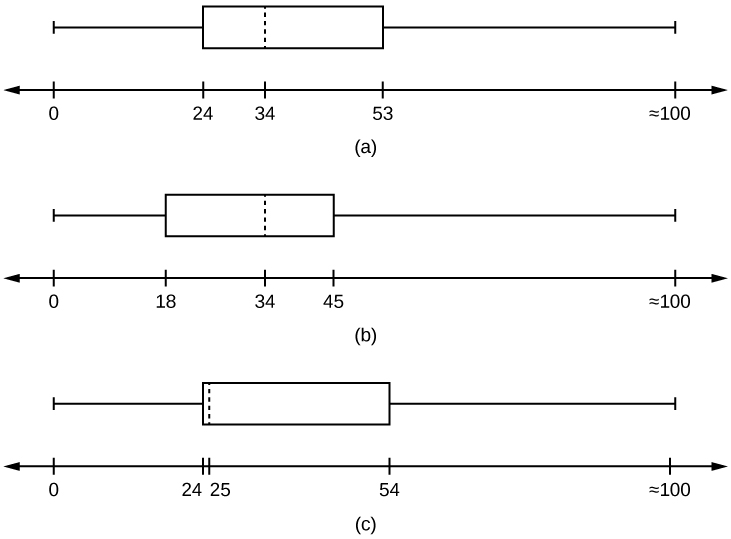
46. Santa Clara County, CA, has approximately 27,873 Japanese-Americans. Their ages are as follows:

Age Group Percent of Community
0–17 18.9
18–24 8.0
25–34 22.8
35–44 15.0
45–54 13.1
55–64 11.9
65+ 10.3
  1. Construct a histogram of the Japanese-American community in Santa Clara County, CA. The bars will not be the same width for this example. Why not? What impact does this have on the reliability of the graph?
  2. What percentage of the community is under age 35?
  3. Which box plot most resembles the information above?
Three box plots with values between 0 and 100. Plot i has Q1 at 24, M at 34, and Q3 at 53; Plot ii has Q1 at 18, M at 34, and Q3 at 45; Plot iii has Q1 at 24, M at 25, and Q3 at 54.

Measures of the Center of the Data

47. Find the mean for the following frequency tables.

  1. Grade Frequency
    49.5–59.5 2
    59.5–69.5 3
    69.5–79.5 8
    79.5–89.5 12
    89.5–99.5 5
  2. Daily Low Temperature Frequency
    49.5–59.5 53
    59.5–69.5 32
    69.5–79.5 15
    79.5–89.5 1
    89.5–99.5 0
  3. Points per Game Frequency
    49.5–59.5 14
    59.5–69.5 32
    69.5–79.5 15
    79.5–89.5 23
    89.5–99.5 2

Use the following information to answer the next three exercises: The following data show the lengths of boats moored in a marina. The data are ordered from smallest to largest: 161719202021232425252526262727272829303233333435373940

48. Calculate the mean.

 49. Identify the median.

50. Identify the mode.

Use the following information to answer the next three exercises: Sixty-five randomly selected car salespersons were asked the number of cars they generally sell in one week. Fourteen people answered that they generally sell three cars; nineteen generally sell four cars; twelve generally sell five cars; nine generally sell six cars; eleven generally sell seven cars. Calculate the following:

51. sample mean = x⎯⎯ = _______

52. median = _______

53. mode = _______

54. The most obese countries in the world have obesity rates that range from 11.4% to 74.6%. This data is summarized in the following table.

Percent of Population Obese Number of Countries
11.4–20.45 29
20.45–29.45 13
29.45–38.45 4
38.45–47.45 0
47.45–56.45 2
56.45–65.45 1
65.45–74.45 0
74.45–83.45 1
  1. What is the best estimate of the average obesity percentage for these countries?
  2. The United States has an average obesity rate of 33.9%. Is this rate above average or below?
  3. How does the United States compare to other countries?

55. The table gives the percent of children under five considered to be underweight. What is the best estimate for the mean percentage of underweight children?

Percent of Underweight Children Number of Countries
16–21.45 23
21.45–26.9 4
26.9–32.35 9
32.35–37.8 7
37.8–43.25 6
43.25–48.7 1

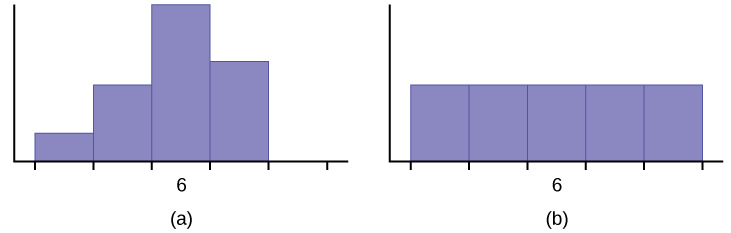
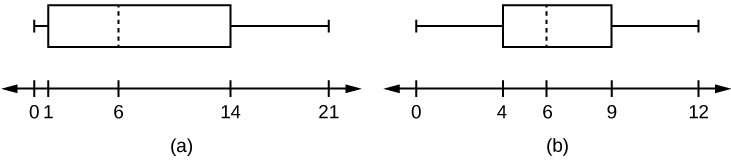
56. Javier and Ercilia are supervisors at a shopping mall. Each was given the task of estimating the mean distance that shoppers live from the mall. They each randomly surveyed 100 shoppers. The samples yielded the following information.

Javier Ercilia
x⎯⎯ 6.0 miles 6.0 miles
s 4.0 miles 7.0 miles
  1. How can you determine which survey was correct ?
  2. Explain what the difference in the results of the surveys implies about the data.
  3. If the two histograms depict the distribution of values for each supervisor, which one depicts Ercilia’s sample? How do you know?
    This shows two histograms. The first histogram shows a fairly symmetrical distribution with a mode of 6. The second histogram shows a uniform distribution.
  4. If the two box plots depict the distribution of values for each supervisor, which one depicts Ercilia’s sample? How do you know?
    This shows two horizontal boxplots. The first boxplot is graphed over a number line from 0 to 21. The first whisker extends from 0 to 1. The box begins at the first quartile, 1, and ends at the third quartile, 14. A vertical, dashed line marks the median at 6. The second whisker extends from the third quartile to the largest value, 21. The second boxplot is graphed over a number line from 0 to 12. The first whisker extends from 0 to 4. The box begins at the first quartile, 4, and ends at the third quartile, 9. A vertical, dashed line marks the median at 6. The second whisker extends from the third quartile to the largest value, 12.

Use the following information to answer the next three exercises: We are interested in the number of years students in a particular elementary statistics class have lived in California. The information in the following table is from the entire section.

Number of years Frequency Number of years Frequency
Total = 20
7 1 22 1
14 3 23 1
15 1 26 1
18 1 40 2
19 4 42 2
20 3
57. What is the IQR?

  1. 8
  2. 11
  3. 15
  4. 35

58. What is the mode?

  1. 19
  2. 19.5
  3. 14 and 20
  4. 22.65

59. Is this a sample or the entire population?

  1. sample
  2. entire population
  3. neither

Skewness and the Mean, Median, and Mode

Use the following information to answer the next three exercises: State whether the data are symmetrical, skewed to the left, or skewed to the right.

60. 11122223333333344455

61. 161719222222222223

62. 87878787878889899091

63. When the data are skewed left, what is the typical relationship between the mean and median?

64. When the data are symmetrical, what is the typical relationship between the mean and median?

65. What word describes a distribution that has two modes?

66. Describe the shape of this distribution.

This is a historgram which consists of 5 adjacent bars with the x-axis split into intervals of 1 from 3 to 7. The bar heights peak at the first bar and taper lower to the right.

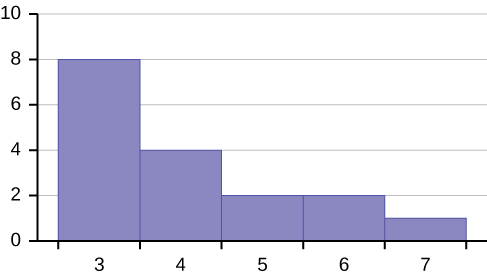
67. Describe the relationship between the mode and the median of this distribution.

This is a histogram which consists of 5 adjacent bars with the x-axis split into intervals of 1 from 3 to 7. The bar heights peak at the first bar and taper lower to the right. The bar ehighs from left to right are: 8, 4, 2, 2, 1.

78. Describe the relationship between the mean and the median of this distribution.This is a histogram which consists of 5 adjacent bars with the x-axis split into intervals of 1 from 3 to 7. The bar heights peak at the first bar and taper lower to the right. The bar heights from left to right are: 8, 4, 2, 2, 1.

79. Describe the shape of this distribution.

This is a histogram which consists of 5 adjacent bars with the x-axis split into intervals of 1 from 3 to 7. The bar heights peak in the middle and taper down to the right and left.

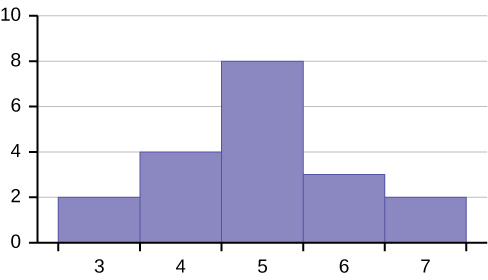
80. Describe the relationship between the mode and the median of this distribution.

This is a histogram which consists of 5 adjacent bars with the x-axis split intervals of 1 from 3 to 7. The bar heights peak in the middle and taper down to the right and left.

81. Are the mean and the median the exact same in this distribution? Why or why not?

This is a histogram which consists of 5 adjacent bars with the x-axis split into intervals of 1 from 3 to 7. The bar heights from left to right are: 2, 4, 8, 5, 2.

82. Describe the shape of this distribution.

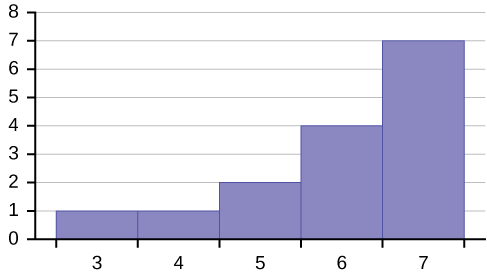
This is a histogram which consists of 5 adjacent bars over an x-axis split into intervals of 1 from 3 to 7. The bar heights from left to right are: 1, 1, 2, 4, 7.

83. Describe the relationship between the mode and the median of this distribution.

This is a histogram which consists of 5 adjacent bars over an x-axis split into intervals of 1 from 3 to 7. The bar heights from left to right are: 1, 1, 2, 4, 7.

84. Describe the relationship between the mean and the median of this distribution.This is a histogram which consists of 5 adjacent bars over an x-axis split into intervals of 1 from 3 to 7. The bar heights from left to right are: 1, 1, 2, 4, 7.

85. The mean and median for the data are the same.

86. 345566667777777,  Is the data perfectly symmetrical? Why or why not?

87. Which is the greatest, the mean, the mode, or the median of the data set?  111112121212131517222222

88. Which is the least, the mean, the mode, and the median of the data set?  5656565859606264646567

89. Of the three measures, which tends to reflect skewing the most, the mean, the mode, or the median? Why?

90. In a perfectly symmetrical distribution, when would the mode be different from the mean and median?

91. The median age of the U.S. population in 1980 was 30.0 years. In 1991, the median age was 33.1 years.

  1. What does it mean for the median age to rise?
  2. Give two reasons why the median age could rise.
  3. For the median age to rise, is the actual number of children less in 1991 than it was in 1980? Why or why not?

Measures of the Spread of the Data

Use the following information to answer the next two exercises:

The following data are the distances between 20 retail stores and a large distribution center. The distances are in miles.  29; 37; 38; 40; 58; 67; 68; 69; 76; 86; 87; 95; 96; 96; 99; 106; 112; 127; 145; 150

92. Use a graphing calculator or computer to find the standard deviation and round to the nearest tenth.

93. Find the value that is one standard deviation below the mean.

94. Two baseball players, Fredo and Karl, on different teams wanted to find out who had the higher batting average when compared to his team. Which baseball player had the higher batting average when compared to his team?

Baseball Player Batting Average Team Batting Average Team Standard Deviation
Fredo 0.158 0.166 0.012
Karl 0.177 0.189 0.015
 95. Use the table to find the value that is three standard deviations:
  • above the mean
  • below the mean

Find the standard deviation for the following frequency tables using the formula. Check the calculations with the TI 83/84.

96. Find the standard deviation for the following frequency tables using the formula. Check the calculations with the TI 83/84.

  1. Grade Frequency
    49.5–59.5 2
    59.5–69.5 3
    69.5–79.5 8
    79.5–89.5 12
    89.5–99.5 5
  2. Daily Low Temperature Frequency
    49.5–59.5 53
    59.5–69.5 32
    69.5–79.5 15
    79.5–89.5 1
    89.5–99.5 0
  3. Points per Game Frequency
    49.5–59.5 14
    59.5–69.5 32
    69.5–79.5 15
    79.5–89.5 23
    89.5–99.5 2
 Use the following information to answer the next nine exercises: The population parameters below describe the full-time equivalent number of students (FTES) each year at Lake Tahoe Community College from 1976–1977 through 2004–2005.
  • μ = 1000 FTES
  • median = 1,014 FTES
  • σ = 474 FTES
  • first quartile = 528.5 FTES
  • third quartile = 1,447.5 FTES
  • n = 29 years

97. A sample of 11 years is taken. About how many are expected to have a FTES of 1014 or above? Explain how you determined your answer.

 98. 75% of all years have an FTES:
at or below: _____
at or above: _____

99. The population standard deviation = _____

100. What percent of the FTES were from 528.5 to 1447.5? How do you know?

101. What is the IQR? What does the IQR represent?

 102. How many standard deviations away from the mean is the median?

Additional Information: The population FTES for 2005–2006 through 2010–2011 was given in an updated report. The data are reported here.

Year 2005–06 2006–07 2007–08 2008–09 2009–10 2010–11
Total FTES 1,585 1,690 1,735 1,935 2,021 1,890

103. Calculate the mean, median, standard deviation, the first quartile, the third quartile and the IQR. Round to one decimal place.

104. Construct a box plot for the FTES for 2005–2006 through 2010–2011 and a box plot for the FTES for 1976–1977 through 2004–2005.

105. Compare the IQR for the FTES for 1976–77 through 2004–2005 with the IQR for the FTES for 2005-2006 through 2010–2011. Why do you suppose the IQRs are so different?

106. Three students were applying to the same graduate school. They came from schools with different grading systems. Which student had the best GPA when compared to other students at his school? Explain how you determined your answer.

Student GPA School Average GPA School Standard Deviation
Thuy 2.7 3.2 0.8
Vichet 87 75 20
Kamala 8.6 8 0.4
107. A music school has budgeted to purchase three musical instruments. They plan to purchase a piano costing $3,000, a guitar costing $550, and a drum set costing $600. The mean cost for a piano is $4,000 with a standard deviation of $2,500. The mean cost for a guitar is $500 with a standard deviation of $200. The mean cost for drums is $700 with a standard deviation of $100. Which cost is the lowest, when compared to other instruments of the same type? Which cost is the highest when compared to other instruments of the same type. Justify your answer.
108. An elementary school class ran one mile with a mean of 11 minutes and a standard deviation of three minutes. Rachel, a student in the class, ran one mile in eight minutes. A junior high school class ran one mile with a mean of nine minutes and a standard deviation of two minutes. Kenji, a student in the class, ran 1 mile in 8.5 minutes. A high school class ran one mile with a mean of seven minutes and a standard deviation of four minutes. Nedda, a student in the class, ran one mile in eight minutes.
  1. Why is Kenji considered a better runner than Nedda, even though Nedda ran faster than he?
  2. Who is the fastest runner with respect to his or her class? Explain why.

The most obese countries in the world have obesity rates that range from 11.4% to 74.6%. This data is summarized in Table 14.

Percent of Population Obese Number of Countries
11.4–20.45 29
20.45–29.45 13
29.45–38.45 4
38.45–47.45 0
47.45–56.45 2
56.45–65.45 1
65.45–74.45 0
74.45–83.45 1

109. What is the best estimate of the average obesity percentage for these countries? What is the standard deviation for the listed obesity rates? The United States has an average obesity rate of 33.9%. Is this rate above average or below? How “unusual” is the United States’ obesity rate compared to the average rate? Explain.

The table gives the percent of children under five considered to be underweight.
Percent of Underweight Children Number of Countries
16–21.45 23
21.45–26.9 4
26.9–32.35 9
32.35–37.8 7
37.8–43.25 6
43.25–48.7 1

110. What is the best estimate for the mean percentage of underweight children? What is the standard deviation? Which interval(s) could be considered unusual? Explain.

111. Twenty-five randomly selected students were asked the number of movies they watched the previous week. The results are as follows:

# of movies Frequency
0 5
1 9
2 6
3 4
4 1
  1. Find the sample mean [latex]overline{x}[/latex].
  2. Find the approximate sample standard deviation, s.

112. Forty randomly selected students were asked the number of pairs of sneakers they owned. Let X = the number of pairs of sneakers owned. The results are as follows:

X Frequency
1 2
2 5
3 8
4 12
5 12
6 0
7 1
  1. Find the sample mean[latex]overline{x}[/latex]
  2. Find the sample standard deviation, s
  3. Construct a histogram of the data.
  4. Complete the columns of the chart.
  5. Find the first quartile.
  6. Find the median.
  7. Find the third quartile.
  8. Construct a box plot of the data.
  9. What percent of the students owned at least five pairs?
  10. Find the 40th percentile.
  11. Find the 90th percentile.
  12. Construct a line graph of the data
  13. Construct a stemplot of the data

113. Following are the published weights (in pounds) of all of the team members of the San Francisco 49ers from a previous year. 177; 205; 210; 210; 232; 205; 185; 185; 178; 210; 206; 212; 184; 174; 185; 242; 188; 212; 215; 247; 241; 223; 220; 260; 245; 259; 278; 270; 280; 295; 275; 285; 290; 272; 273; 280; 285; 286; 200; 215; 185; 230; 250; 241; 190; 260; 250; 302; 265; 290; 276; 228; 265

  1. Organize the data from smallest to largest value.
  2. Find the median.
  3. Find the first quartile.
  4. Find the third quartile.
  5. Construct a box plot of the data.
  6. The middle 50% of the weights are from _______ to _______.
  7. If our population were all professional football players, would the above data be a sample of weights or the population of weights? Why?
  8. If our population included every team member who ever played for the San Francisco 49ers, would the above data be a sample of weights or the population of weights? Why?
  9. Assume the population was the San Francisco 49ers. Find:
    1. the population mean, μ.
    2. the population standard deviation, σ.
    3. the weight that is two standard deviations below the mean.
    4. When Steve Young, quarterback, played football, he weighed 205 pounds. How many standard deviations above or below the mean was he?
  10. That same year, the mean weight for the Dallas Cowboys was 240.08 pounds with a standard deviation of 44.38 pounds. Emmit Smith weighed in at 209 pounds. With respect to his team, who was lighter, Smith or Young? How did you determine your answer?

114. One hundred teachers attended a seminar on mathematical problem solving. The attitudes of a representative sample of 12 of the teachers were measured before and after the seminar. A positive number for change in attitude indicates that a teacher’s attitude toward math became more positive. The 12 change scores are as follows:

3 8–12 05–31–16 5–2

  1. What is the mean change score?
  2. What is the standard deviation for this population?
  3. What is the median change score?
  4. Find the change score that is 2.2 standard deviations below the mean.

115. Refer to the figure to determine which of the following are true and which are false. Explain your solution to each part in complete sentences.

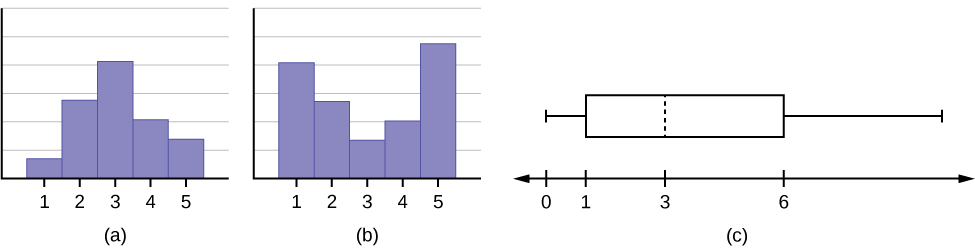
This shows three graphs. The first is a histogram with a mode of 3 and fairly symmetrical distribution between 1 (minimum value) and 5 (maximum value). The second graph is a histogram with peaks at 1 (minimum value) and 5 (maximum value) with 3 having the lowest frequency. The third graph is a box plot. The first whisker extends from 0 to 1. The box begins at the firs quartile, 1, and ends at the third quartile,6. A vertical, dashed line marks the median at 3. The second whisker extends from 6 on.
  1. The medians for all three graphs are the same.
  2. We cannot determine if any of the means for the three graphs is different.
  3. The standard deviation for graph b is larger than the standard deviation for graph a.
  4. We cannot determine if any of the third quartiles for the three graphs is different.
 116. In a recent issue of the IEEE Spectrum, 84 engineering conferences were announced. Four conferences lasted two days. Thirty-six lasted three days. Eighteen lasted four days. Nineteen lasted five days. Four lasted six days. One lasted seven days. One lasted eight days. One lasted nine days. Let X = the length (in days) of an engineering conference.
  1. Organize the data in a chart.
  2. Find the median, the first quartile, and the third quartile.
  3. Find the 65th percentile.
  4. Find the 10th percentile.
  5. Construct a box plot of the data.
  6. The middle 50% of the conferences last from _______ days to _______ days.
  7. Calculate the sample mean of days of engineering conferences.
  8. Calculate the sample standard deviation of days of engineering conferences.
  9. Find the mode.
  10. If you were planning an engineering conference, which would you choose as the length of the conference: mean; median; or mode? Explain why you made that choice.
  11. Give two reasons why you think that three to five days seem to be popular lengths of engineering conferences.

117. A survey of enrollment at 35 community colleges across the United States yielded the following figures:

6414; 1550; 2109; 9350; 21828; 4300; 5944; 5722; 2825; 2044; 5481; 5200; 5853; 2750; 10012; 6357; 27000; 9414; 7681; 3200; 17500; 9200; 7380; 18314; 6557; 13713; 17768; 7493; 2771; 2861; 1263; 7285; 28165; 5080; 11622

  1. Organize the data into a chart with five intervals of equal width. Label the two columns “Enrollment” and “Frequency.”
  2. Construct a histogram of the data.
  3. If you were to build a new community college, which piece of information would be more valuable: the mode or the mean?
  4. Calculate the sample mean.
  5. Calculate the sample standard deviation.
  6. A school with an enrollment of 8000 would be how many standard deviations away from the mean?

Use the following information to answer the next two exercises.

X = the number of days per week that 100 clients use a particular exercise facility.

x Frequency
0 3
1 12
2 33
3 28
4 11
5 9
6 4
118. The 80th percentile is _____

  1. 5
  2. 80
  3. 3
  4. 4

119. The number that is 1.5 standard deviations BELOW the mean is approximately _____

  1. 0.7
  2. 4.8
  3. –2.8
  4. Cannot be determined

120. Suppose that a publisher conducted a survey asking adult consumers the number of fiction paperback books they had purchased in the previous month. The results are summarized in the table.

# of books Freq. Rel. Freq.
0 18
1 24
2 24
3 22
4 15
5 10
7 5
9 1
  1. Are there any outliers in the data? Use an appropriate numerical test involving the IQR to identify outliers, if any, and clearly state your conclusion.
  2. If a data value is identified as an outlier, what should be done about it?
  3. Are any data values further than two standard deviations away from the mean? In some situations, statisticians may use this criteria to identify data values that are unusual, compared to the other data values. (Note that this criteria is most appropriate to use for data that is mound-shaped and symmetric, rather than for skewed data.)
  4. Do parts a and c of this problem give the same answer?
  5. Examine the shape of the data. Which part, a or c, of this question gives a more appropriate result for this data?
  6. Based on the shape of the data which is the most appropriate measure of center for this data: mean, median or mode?

License

Icon for the Creative Commons Attribution 4.0 International License

Section Exercises Copyright © 2018 by Barbara Illowsky & OpenStax et al. is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book